Индивидуальная карточка учащегося.

Задание: составить рисунок-схему и математическую модель задачи.

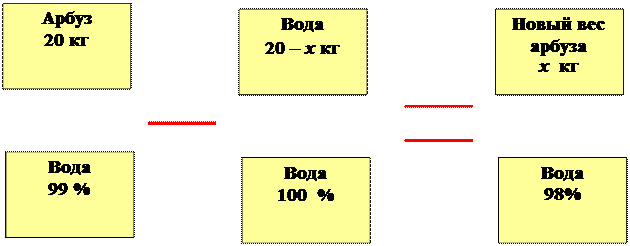
1 ЗАДАЧА : Арбуз весил 20 кг и содержал 99% воды, когда он немного усох, то стал содержать 98% воды. Сколько теперь весит арбуз?

Составляем уравнение:

99 * 20 – 100 * ( 20 – х ) = 98 х

2 ЗАДАЧА : Даны 2 куска с различньм содержанием олова. Первый массой 300 г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько % олова будет содержать

Сплав, полученный из этих кусков

Составляем уравнение:

300 * 20 + 200 * 40 = 500 х

1. Постановка домашнего задания.

Решить различными способами №643.

1. Подведение итогов работы на уроке.

Дети заполняют карточки самооценки.

Вид работы на уроке	Домашнее задание	Участие в обсуждении нового метода (визуально-графической поддержки)	Самостоятельная работа по карточкам	Итог
Оценка

I I I.Заключение

Покажем превосходство визуально-графического метода по сравнению с алгебраическим на примере конкурсной задачи.

Задача. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось ещё в руде?

Алгебраический способ решения:

	Масса руды, в кг	Масса железа, в кг	Концентрация (доля железа в руде)
Руда		х кг	х /500
Руда после удаления примесей	500-200=300	х – 0,12 * 200= х - 25	х – 25 / 300

1) 500 – 200 = 300 (кг) – масса руды после удаления примесей.

2) 0,125 * 200 = 25 (кг) – масса железа в 200 кг примесей.

Пусть

х кг - масса железа в руде,

(х – 25) кг – масса железа в руде после удаления примесей.

х / 500 – доля железа в руде,

х - 25 / 300 – доля железа в руде после удаления примесей.

По условию, содержание железа в оставшейся руде повысилось на 20% = 0,2.

Составим уравнение:

х - 25				х

5 (х-25)				3х
1 500		1 500	1 500

5х – 125-300-3х = 0,

2х = 425,

х = 212,5.

212,5 кг – масса железа в руде.

3) 212,5 – 25 = 187,5 (кг) – железа осталось в руде после удаления примесей.

Ответ: 187,5 кг.

Метод визуально-графической поддержки:

	Руда 500 кг		Примеси 200 кг		Оставшаяся руда 300 кг

Руда 500 кг

	Железо х %		Железо 12,5%		Железо х + 20%

500 х – 200 * 12.5 = 300 (х + 20)

500х – 2 500 = 300х + 6000

200х = 8 500

х = 42,5

42,5 + 20 = 62,5 % - содержание железа в оставшейся руде.

62,5 х 300 = 187,5 (кг) – осталось железа в руде после удаления примесей.

Ответ: 187,5 кг.

Итак, сравним первый этап решения задачи: перевода условия задачи с математического языка на обычный. При визуально-графическом методе словесно это звучит так: из 500кг руды удалили 200 кг примесей, получили 300 кг оставшейся руды. Руда содержит х% железа, примеси 12,5% железа, а оставшаяся руда (х+20) % железа Входе перевода задачи появляется схема. И этого достаточно , чтобы получилась математическая модель. А при алгебраическом методе требуется умение находить дробь от числа, затем долю железа в руде до и после удаления примесей, а это вызывает затруднения у школьников. Далее получается дробное уравнение. А оно сложнее линейного.

Первый этап при визуально графическом методе решения текстовых задач проще, короче. нагляднее. Для изучения математики большое значение имеет зрительная память.

Далее. преимущество этого метода- он охватывает широкий спектр задач: на концентрацию. процентное содержание, сплавы. выветривание. усыхание т. е. все .кроме «банковских».

Этот метод можно применять и в смежных дисциплинах: химии, физике. Биологии. Географии. Самостоятельный перенос приемов деятельности в новые ситуации- это черта творческой деятельности учащегося. И все это позволяет выполнить метод визуально-графической поддержки.

IV.Приложение

Задачи для самостоятельного решения

Задача 1

В 500 кг руды содержится некоторое количество железа . После удаления из руды 200кг примесей, содержащих в среднем 12.5% железа. Содержание железа в оставшейся руде повысилось на 20%.Определите, какое количество железа осталось еще в руде?

Ответ: 187.5 кг.

Задача 2.

Сколько воды нужно вы парить из 40 кг 20% раствора соли , чтобы получить 25% раствор этой соли?

Ответ: 8кг.

Задача 3.

Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?

Ответ: 70 кг.

Задача 4.

Смешали 30% раствор соляной кислоты с 10% и получили 600 г 15 % раствора. Сколько граммов каждого раствора было взято?

Ответ: 150 г и 450 г.

Задача 5

Кусок сплава массой 36 кг содержит 45 % меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60 % меди?

Ответ: 13,5кг.

Задача 6.

Имеется два сплава меди с разным содержанием меди. Число ,выражающее в процентах содержание меди в первом сплаве, на 40 меньше числа, выражающего в процентах содержание меди во втором сплаве. Оба эти сплава сплавили вместе, после чего содержание меди составило 36 процентов. Определить процентное содержание меди в первом и во втором сплавах, если известно, что в первом сплаве меди было 6 кг , а во втором -12кг.

Ответ: 20% и 60%.

Задача 7.

Имеется кусок сплава меди с оловом общей массой 12 кг, содержащей 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

Ответ: 1,5 кг

Задача 8.

В бидон налили 3 литра молока 1% жирности и 7 литров молока 6 % жирности. Какова жирность, полученного молока ?

Ответ: 4,5 %.

Задача 9.

Торговец продает орехи двух сортов одни по 90 центов другие по 60 центов за кг. Он хочет получить 50 кг смеси по 72 цента за кг. Сколько для этого потребуется орехов каждого сорта?

Ответ: 20 кг и 30 кг.

Задача 10.

Сколько граммов воды можно выпарить из 80г 6 % раствора соли. Чтобы получить раствор содержащий 10 % соли?

Ответ: 32 г.

Задача 11.

Имеется два кислотных раствора: один 20 %., другой 30 %. Взяли 0.5 л первого и 1,5 л второго и образовали новый раствор. Какова концентрация кислоты в новом растворе?

Ответ: 27.5 %

Задача 12.

Смешали 300 г 50 % и 100 г 30 % раствора кислоты. Определите процентное содержание кислоты в полученной смеси.

Ответ:45 %.

Задача 13.

Сколько чистой воды надо добавить к 300 г морской воды. Содержащей 4 5 соли. Чтобы получить воду, содержащую 3 5 соли?

Задача 14.

Имеется два сосуда. содержащие 4 кг и 6 кг раствора кислоты различной концентрации. Если их слить вместе. То получим раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов. То получим раствор, содержащий 36% кислоты. Сколько кг кислоты содержится в каждом растворе?

Ответ: 1.64 кг и 1.86 кг

Задача 15.

Имеются две смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока , а вторая 80%. Смешиваются х л первой смеси и у л второй, в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите х и у.

Ответ: х = 5 у = 15 л .