Спектр аналитического сигнала

является односторонним (рис.2.6б)

.(2.4.11)

Спектр комплексной огибающей сигнала согласно (8) повторяет спектр аналитического сигнала со сдвигом на несущую частоту f₀ (рис.2.6в)

.(2.4.12)

Заметим что спектры комплексных сигналов и 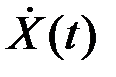в общем случае не обладают свойством симметрии (рис.2.6б, 2.6в). Выбор несущей (центральной) частоты удобно производить в спектральной области. Обычно это среднее значение (центр тяжести) боковой полосы или мода этой полосы. Если спектр аналитического сигнала симметричная функция, обе характеристики совпадают и выбор f₀ практически однозначен.

Приведем некоторые соотношения для аналитического сигнала и его квадратурных составляющих, облегчающие многие аналитические преобразования в теории РТС.

- Умножая правую и левую часть (10) на jsgn(f), получаем

(2.4.13)

Это значит, что обратное преобразование Гильберта

(2.4.14)

отличается от прямого только знаком.

- Квадратурные сигналы взаимно ортоганальны

. (2.4.15)

- Формулы Парсеваля для преобразования Гильберта

(2.4.16)

(2.4.17)

Формулы проверяются непосредственным счетом с использованием прямого и обратного преобразования Гильберта или переходом в спектральную область. Например,

- Далее для сокращения выражений аргумент t опущен

(2.4.18)

Поэтому, в частности,

(2.4.19)

- Наконец согласно (16) и (17)

(2.4.20)

Аналогично

(2.4.21)

2.5. Линейные инвариантные во времени (ЛИВ) системы

Математическая модель информационной системы определяется оператором системы L, отображающим множество входных сигналов {u(t)} на множество выходных сигналов {u(t)} (рис.2.7)

.(2.5.1)

Рис. 2.7

Существуют различные типы и соответственно модели информационных систем. Мы ограничиваем рассмотрение используемыми в дальнейшем динамическими ЛИВ системами. В динамической (или инерционной) системе выходной сигнал (выход) u(t) в момент наблюдения t зависит от значений входного сигнала (входа) u(t) не только в момент t, но и в предшествующие моменты времени. Будет рассматриваться модель типа "черного ящика", при которой внутреннее строение и состояние системы не затрагивается, но полагается заданным вход u(t) на всем предшествующем интервале tÎ(-¥, t). Инвариантность во времени (стационарность) системы означает, что оператор системы L (или ее характеристики) во времени не меняются. Наконец, линейная - это значит, что она подчиняется принципу суперпозиции: если u_i(t)=L [u_i(t)], i=1,...,n , то

(2.5.2)

где a₁,...,a_n - произвольные коеффициенты. Реакция на сумму воздействий равна сумме соответствующих реакций.

Анализ и синтез ЛИВ-систем, как и сигналов, может производиться во временной или частотной области. Во временной области ЛИВ-система характеризуется импульсной характеристикой h(t) - рекцией системы u(t)=h(t) на входное воздействие в виде дельта-функции u(t)=d(t). Для практического определения импульсной характеристики h(t) на вход системы подается в момент времени t=0 короткий (по сравнению с постоянной времени системы) импульс с единичной площадью d_D(t). Вследствие того, что система инвариантна во времени, ее реакция на сдвинутое воздействие d(t-x) будет иметь прежний вид h(×) и тот же сдвиг h(t-x).

Определим теперь оператор системы. В соответствии с (2.3.4) свертка d(t) с произвольной, в частности с входной функцией u(t), воспроизводит последнюю

.(2.5.3)

Линейное преобразование (3) представляет собой предел суммы В соответствии с принципом суперпозиции (2) выход u(t) будет определяться аналогичным преобразованием, в котором нужно только заменить воздействие d(t-x_i) на соответствующую реакцию системы h(t-x_i). В результате получаем оператор системы u(t)=L[u(t)] в виде линейного интегрального преобразования типа свертки

(2.5.4)

Реакция h(t) реальной физической системы не может возникнуть раньше воздействия d(t). Математически эта закономерность выражается условием физической реализуемости системы

(2.5.5)

Пределы интегрирования в (4) для физически реализуемых систем можно проставить с учетом (5)

(2.5.6)

Вместе с тем в теоретических исследованиях часто используются системы, не подчиняющиеся условию (5). Это условие может, например, не выполняться в системах обработки сигналов, использующих вычислительную технику (цифровая обработка сигналов с запаздыванием). Мы будем пользоваться более общей формулой (4).

В частотной области оператору системы - свертке (4) соответствует произведение спектров

, (2.5.7)

где

(2.5.8)

комплексный коэффициент передачи системы (частотная характеристика, системная функция), |K(f)| - амплитудно-частотная характеристика (АЧХ), argK(f) - фазо-частотная характеристика (ФЧХ). Таким образом, основными характеристиками ЛИВ-системы являются импульсная h(t) и частотная K(f) характеристики, связанные между собой взаимно однозначно преобразованием Фурье

. (2.5.9)

Из соображений удобства выбирают в каждом конкретном случае, какой из них следует пользоваться.

В заключение отметим, что для характеристики динамических линейных систем с изменяющимися во времени параметрами также используется импульсная характеристика h(t,t), но являющаяся функцией двух моментов времени t и t. Характеристика h(t,t) это реакция системы в момент t на воздействие d(t-t) в виде d-функции, поданное в момент времени t=t. Последнее определение, являясь более общим, годится и для ЛИВ-систем. При этом

. (2.5.10)

Рассмотрение, аналогичное приведенному выше, позволяет получить оператор линейной изменяющейся во времени системы

. (2.5.9)