Общие указания к выполнению лабораторных работ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным работам по дисциплине

«Автоматизированные системы управления и связь»

Уфа 2016

Составитель: А.М.Пугин

УДК 621.38

ББК 32.85

Г96

Лабораторный практикум по дисциплине «Автоматизированные системы управления и связь» для студентов по направлению подготовки дипломированного специалиста 20.00.00 – “ТЕХНОСФЕРНАЯ БЕЗОПАСНОСТЬ И ПРИРОДООБУСТРОЙСТВО” специальности – 20.05.01 “Пожарная безопасность” (заочной формы обучения) / Уфимск. гос. авиац. техн. ун-т; Сост. А.М. Пугин – Уфа, 2016. 26 - с. Табл. 1. Ил.10. Библиогр.:6 назв.

Содержание

Введение ………………………………………………….…..……….………..…..
Лабораторная работа № 1. Определение статических характеристик типовых звеньев и системы автоматического управления ……………....….….
Лабораторная работа № 2.Определение временных характеристик типовых звеньев и системы автоматического управления …..………….….......................

Введение

Данные методические указания составлены на основании учебных планов по изучению дисциплины «Автоматизированные системы управления и связь» и включают в себя задания к проведению двух лабораторных работ.

Исследование систем автоматического управления может заключаться в решении одной из двух задач – задачи анализа и задачи синтеза. В первом случае дается система, включая значение параметров, и требуется определить ее свойства. Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям. Очевидно, что задача синтеза много сложнее анализа уже из-за ее неоднозначности.

Математическое описание системы начинается с разбиения ее на звенья (в лабораторных работах звенья уже заданы) и описание этих звеньев. Последнее может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих эту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система. Известно, что любое движение, процессы передачи, обмена и преобразования энергии или вещества математически описываются дифференциальными уравнениями. Работу САУ также принять описывать дифференциальными уравнениями, которые определяют сущность процессов в системе независимо от принципов ее действия, назначения и конструкции. Решив дифференциальное уравнение системы, можно найти характер изменения управляемой переменной в переходных и установившихся режимах при определенных задающих и возмущающих воздействиях на систему. Кроме того, при универсальном едином способе описания работы САУ с помощью дифференциальных уравнений появляется возможность разрабатывать общие методы количественной и качественной оценки процессов управления различных систем.

Динамические свойства линейных звеньев и систем автоматического управления могут быть описаны как дифференциальными уравнениями так и графическими характеристиками. В теории автоматического управления применяются два типа таких характеристик – переходные и частотные. Эти характеристики могут быть определены экспериментальным путем или построены по уравнениям звеньев. Переходные и частотные характеристики однозначно связаны с уравнением звена и наряду с ним являются исчерпывающим описанием динамических свойств звена. Однако процесс нахождения дифференциального уравнения системы через уравнения ее элементов в общем случае является довольно трудоемким. Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления в частности преобразований Лапласа. Преобразование дифференциальных уравнений по Лапласу является основой чрезвычайно удобного для исследований САУ метода передаточных функций. С помощью передаточных функций можно легко оценить динамические свойства любого элемента САУ. Расчет САУ существенно упрощается и не требует применения сложного математического аппарата. Поэтому метод передаточных функций является основой инженерных расчетов САУ, в том числе и для расчетов системы управления рассматриваемой в данных лабораторных работах.

Лабораторные работы, представленные в данном методическом указании, являются расчетно-исследовательскими и предполагают проведение в полном объеме анализа статики и динамики системы автоматического управления и отдельных ее звеньев. Объектом исследования является следящая система, структурная схема которой представлена на рисунке В.1. Исходные данные для расчета приведены в таблице В.1.

Каждый студент получает номер варианта исходных данных от преподавателя. По каждой лабораторной работе студент составляет индивидуальный отчет, содержащий результаты расчетов в виде таблиц и графиков с необходимыми пояснениями и выводами. После выполнения и оформления всех работ отчеты по ним следует сброшюровать и сделать общие выводы по исследуемой системе.

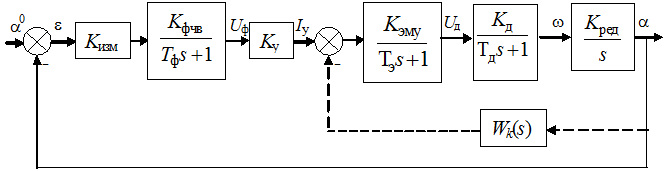
Рисунок В.1 - Структурная схема следящей системы

На схеме К_изм - передаточный коэффициент измерительного устройства; К_фчв, Т_ф - коэффициент передачи и постоянная времени фазочувствительного выпрямителя; К_у - коэффициент усиления электронного усилителя; К_эму, Т_э - коэффициент передачи и постоянная времени электромашинного усилителя; К_д, Т_д - коэффициент усиления и постоянная времени электрического двигателя; К_ред - коэффициент передачи редуктора.

Лабораторная работа № 1

Цель работы

Теоретическая часть

Как динамическая система, САУ может работать в одном из двух режимов – в стационарном (установившемся) и в переходном. Поэтому в общем виде порядок исследования САУ в обоих случаях включает математическое описание системы, исследование ее стационарных (установившихся) и переходных режимов.

Стационарный режим может быть статическим и динамическим.

Статический стационарный режим (статика) – это режим, при котором система находится в состоянии покоя вследствие того, что все внешние воздействия и параметры самой системы не меняются во времени

Динамический стационарный режим возникает, когда приложенные к системе внешние воздействия изменяются по какому-либо установившемуся закону, в результате чего система приходит в режим установившегося вынужденного движения.

Статические характеристики определяют зависимость между выходной и входной величинами звена или системы в установившемся состоянии. Характеристики могут быть получены экспериментальным путем или же в результате аналитических или графо-аналитических расчетов. Знание характеристик звеньев и САУ необходимо для оценки их свойств, анализа и синтеза систем с требуемым качеством функционирования.

2.1. Статические звенья.Статическая характеристика типового звена САУ – это зависимость установившегося значения выходной величины X_уст. от установившегося значения входной величины y_уст.

X_уст. = f_ст. (y_уст.), (1)

где X_уст. – установившееся значение выходной величины; Y_уст. – установившееся значение входной величины; f - в общем случае произвольная нелинейная функция.

Звенья, имеющие такие зависимости, называются статическими.

Статическую характеристику линейного звена (системы), имеющего передаточную функцию 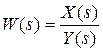, можно получить, используя теорему Лапласа о предельном значении оригинала

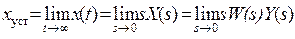, (2)

где W(0) – значение передаточной функции при s = 0, которое равно статическому коэффициенту передачи линейного звена (системы).

Для звена с линейной характеристикой зависимость (1) упрощается:

X_уст. = Кy_уст.. (3)

Если у звена несколько входных величин, то

X_уст. = f_n (y_уст.1, y_уст.2, …, y_уст.n). (4)

Если

X_уст. = f₂ (y_уст.1, y_уст.2.), (5)

то статическая характеристика геометрически становится поверхностью соответствующего измерения. Зависимость вида

X_уст. = f_а (y_уст., а), (6)

где а – параметр настройки, отображает семейство характеристик, каждая из которых соответствует своему значению а.

Статические характеристики могут быть выражены аналитической (1) - (6) или графической зависимостями. Статические характеристики систем (соединений) можно найти по известным статическим характеристикам образующих эти системы звеньев.

2.2.Последовательное соединение звеньев.Рассмотрим, например, определение статической характеристики последовательно соединенных трех звеньев – рисунок 1. Входная величина первого звена является входной величиной соединения (системы), выходная величина первого звена является входной величиной второго звена и т.д. Выходная величина последнего звена является выходной величиной соединения.

X уст.2 = y уст.3

X уст.1 = y уст.2

X уст.3 = X уст.

y уст. = y уст.1

W3(0)

W2(0)

W1(0)

Рисунок 1 – Последовательное соединение звеньев

Структурные преобразования соединения звеньев сохраняют силу для их статических пределов. Поэтому общий коэффициент для последовательного соединения звеньев равен

k = k₁k₂…k_m. (7)

2.3.Параллельное соединение звеньев.В этом случае входная величина соединения (системы) является одновременно входным сигналом для каждого звена – рисунок 2. Результирующая выходная величина соединения (системы) равна сумме выходных сигналов отдельных звеньев.

k = k₁ + k₂ +…+ k_m. (8)

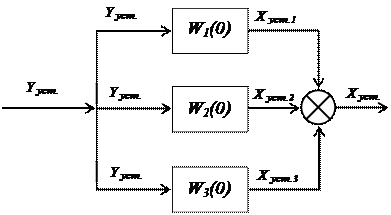
Рисунок 2 – Параллельное соединение звеньев

Последовательно-параллельное соединение звеньев.При таком соединении звеньев на вход звена одновременно с входной величиной подается ее выходная величина, преобразованная звеном обратной связи W_о.с.(s), как показано на рисунке 3.а.

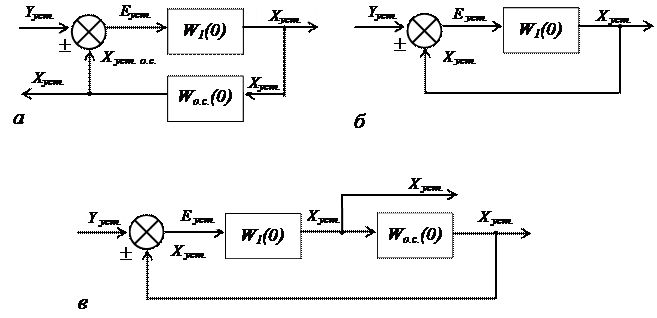
Рисунок 3 – Последовательно-параллельное соединение звеньев

a – параллельное расположение звеньев;

б – соединение с единичной обратной связью;

в – последовательное расположение звеньев

Как видно из схемы на вход звена в прямой цепи поступает разность между входной величиной соединения y_уст. и выходной величиной звена обратной связи x_{уст. о.с.}

e_уст. = y_уст. ± x_{уст. о.с.} (9) Для звена с усилением k₁,охваченного обратной связью с коэффициентом усиления k_о.с.

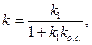(10)

При известной передаточной функции системы нет необходимости рассматривать статические пределы отдельных звеньев. Предельный коэффициент усиления k_р для разомкнутой системы определяют по формуле

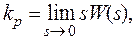(11)

а коэффициент усиления k_з для замкнутой системы

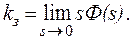(12)

В установившемся режиме структурная схема САУ остается прежней, однако звенья ее становятся динамически неразличимыми. Так, если передаточные функции трех звеньев: колебательного, апериодического и пропорционального имеют вид:

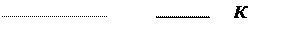К , К ,

T₁²s² +2T₂s +1 T₁s +1

то в установившемся режиме, когда оператор s ® 0, все звенья будут описываться только коэффициентом К. Приведенные формулы справедливы для систем без включенных последовательно интегрирующих звеньев.

Астатические и статические звенья.Не у всех звеньев имеется зависимость между установившимся значением выходной величины от установившегося значения входной величины. Примером может служить электродвигатель, если за его входную величину принять подводимое напряжение, а за выходную – угол поворота якоря. При подаче на электродвигатель напряжения угол поворота его якоря будет увеличиваться непрерывно с определенной скоростью. Такое звено статической характеристики не имеет. Такие звенья называются астатическими. У астатических звеньев при постоянном входном воздействии сигнал на выходе в установившемся режиме непрерывно растет с постоянной скоростью, ускорением и т.д. Для них существует другая статическая зависимость - между установившемся значением скорости выходной величины и установившемся значением входной величины

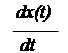= f_аст.(Y_уст.). (13)

Некоторые астатические звенья имеют постоянной не первую производную, а вторую, третью и т.д. В этом случае такие звенья обладают астатизмом второго, третьего и т.д. порядка. Признак того, что звено (или система в целом) является астатическим – это наличие комплексного переменного p в качестве сомножителя в знаменателе передаточной функции.

=

Если в передаточной функции звена (или системы)

W(s)=

Q(s) P(s)

bm sm +sb(m-1) s(m-1)+ …+ s1 p + b0 an sn + a(n-1) s(n-1) + …+ a1 s + a0

. (14)

коэффициенты а₀, а₁, …, а_(n-1) будут равны нулю, то передаточная функция примет вид:

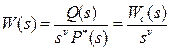, (15)

где

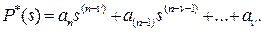(16)

Отсюда видно, что звено с передаточной функцией (15) можно представить в виде последовательного соединения n интегрирующих звеньев с передаточными функциями W_и(s)=1/s и звена с передаточной функцией ,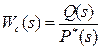

не содержащего последовательных интегрирующих и дифференцирующих элементов и имеющих коэффициент передачи k_c = b₀/a_n . Звенья с передаточной функцией вида W_c(s) являются статическими, так как при поступлении на их вход постоянной величины y_уст. установившееся значение выходной величины будет постоянным и равным

X_уст. = k_c y_уст. (17)

Это следует из того, что после поступления на вход звена с передаточной функцией W_c(s) постоянного воздействия по окончании переходного процесса все производные от выходной величины будут равны нулю. В статическом звене или системе величина W_c(0) равна передаточному коэффициенту

W_c(0) = k_c. (18)

kи s

Интегрирующее звено

W_и(s) = (19)

является астатическим, так как при поступлении на его вход постоянной величины y_уст. выходная величина будет беспрерывно возрастать

x = k_и y_уст.t (20)

с постоянной скоростью

dx/dt = k_и y_уст.. (21)

Таким образом, интегрирующее звено имеет постоянную первую производную от выходной величины при поступлении на его вход постоянного сигнала и, следовательно, обладает астатизмом первого порядка. Так как передаточная функция исходного звена (15) содержит n последовательно соединенных астатических звеньев первого порядка, то оно в целом является астатическим звеном n-го порядка. То есть, порядок астатизма по виду передаточной функции звена или соединения определяется степенью сомножителя p в ее знаменателе. Если за выходную величину такого звена принять производную dⁿx/dtⁿ = x⁽ⁿ⁾(t), то такое звено будет статическим, т.е.

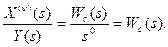(22)

В отношении же всех производных выходной величины более низких порядков это звено будет астатическим

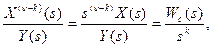(23)

где k = 1, 2, …, n - 1 – порядок астатизма, причем, чем ниже порядок производной выходной величины, тем выше порядок астатизма звена, если эту производную принимать за новую выходную величину.

В общем случае система астатизма n без установившейся ошибки отрабатывает задающие воздействия, описываемые в функции времени выражением

y(t) = 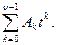(24)

Порядок выполнения работы

3.1.К выполнению лабораторной работы рекомендуется приступать только после внимательного ознакомления с теоретическим разделом настоящих методических указаний.

3.2. Письменно ответить на контрольные вопросы к лабораторной работе. Отчет с ответами (остается у студента) утвердить у преподавателя.

3.1. В исследуемой следящей системе (рис.1) по передаточным функциям элементов определить тип каждого динамического звена и построить его статическую характеристику по данным из таблицы 1.

3.2. Построить статическую характеристику системы в разомкнутом состоянии.

3.3. Построить статическую характеристику системы в замкнутом состоянии. Параметры корректирующего устройству взять из таблицы 2.

3.4. Оформить выполненную работу в виде отчета в соответствии с требованиями ГОСТа 2.105-95. Отчет выполнять на листах формата А4 (210х297 мм). Листы должны иметь штамп для текстовых документов (форма 2а, ГОСT 2.104-68).

3.5. Защитить выполненную работу у преподавателя и сдать отчет.

3.6. Все приведенные выше разделы лабораторной работы выполняются непосредственно в отведенное на лабораторную работу время (4 учебных часа).

Требования к содержанию отчета

Отчет по лабораторной работе должен содержать:

1. Ответы на контрольные вопросы к лабораторной работе.

2. Структурную схему исследуемой системы.

3. Исходные данные (с указанием варианта) для расчета, сведенные в таблицу.

4. Статические характеристики всех элементов системы (X_уст. = f(Y_уст.)).

5. Статическую характеристику системы в разомкнутом состоянии.

6. Статическую характеристику системы в замкнутом состоянии.

5. Контрольные вопросы

1. В каких режимах может работать САУ как динамическая система?

2. Дать определение статическому стационарному режиму работы.

3. Дать определение динамическому стационарному режиму работы.

4. Как определяют статические характеристики звена или системы?

5. Теорема Лапласа о предельном значении оригинала для получения статической характеристики линейного звена (системы).

6. Статическая характеристика звена с несколькими входными величинами?

7. Как графически определяется статическая характеристика соединения из нескольких последовательно соединенных звеньев?

8. Как графически определяется статическая характеристика соединения из нескольких параллельно соединенных звеньев?

9. Как графически определяется статическая характеристика соединения из нескольких последовательно-параллельно соединенных звеньев?

10. Дать определение астатическому звену (системе).

11. Что такое порядок астатизма звена (системы) и как он определяется?

Лабораторная работа № 2

Цель работы

Целью работы является изучение временных характеристик типовых динамических звеньев и методов их графического построения по заданным передаточным функциям.

Теоретическая часть

Динамические свойства линейных звеньев и систем автоматического управления могут быть описаны как дифференциальными уравнениями, так и графическими характеристиками. Процесс нахождения дифференциального уравнения системы через уравнения ее элементов в общем случае является довольно трудоемким. Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления в частности преобразований Лапласа. Преобразование дифференциальных уравнений по Лапласу является основой чрезвычайно удобного для исследований САУ метода передаточных функций. С помощью передаточных функций можно легко оценить динамические свойства любого элемента САУ.

2.1. Передаточной функцией W(s) звена (системы) называется отношение преобразования по Лапласу выходной координаты X(s) звена (системы) к изображению по Лапласу входной координаты Y(s) при нулевых начальных условиях:

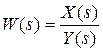. (1)

Под временными характеристиками динамического звена (системы) в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе звена из одного равновесного состояния в другое. Так как дифференциальное уравнение тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика представляет собой графическую форму решения дифференциального уравнения звена для принятого типового воздействия и, следовательно, полностью характеризует динамические свойства звена (системы).

2.2. Временные характеристики могут быть получены не только путем решения дифференциального уравнения системы, но и экспериментальным путем. Это имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение, что является в общем случае очень трудоемкой, а иногда и неразрешимой задачей. Временные характеристики прежде всего зависят от внешнего воздействия (входного воздействия y(t) или возмущения f(t)). Обычно в линейных звеньях при определении временных характеристик по какому-либо одному из внешних воздействий все другие внешние воздействия полагаются равными нулю. Законы изменения внешних воздействий заранее, как правило, неизвестны, т.е. представляют собой случайные функции времени. Поэтому для исследования САУ используются так называемые типовые законы изменения внешних воздействий. Каждому такому типовому закону соответствует своя временная характеристика (функция). Рассмотрим основные типовые воздействия и соответствующие им переходные (временные характеристики).

2.2.1.Переходная функция, илипереходная характеристика, h(t) описывает переходной процесс на выходе звена (системы), возникающий при подаче на его вход скачкообразного воздействия, которое мгновенно возрастает от нуля до единицы и далее остается неизменным при нулевых начальных условиях.

2.2.2. Единичная ступенчатая функция 1(t).Типовое входное воздействие, при котором функция y(t)=1(t) определяется соотношениями y(t) =0 при t < 0 и y(t) =1 при t³ 0, т.е.

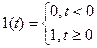(2)

называется единичной ступенчатой функцией 1(t) – рисунок 1а. Предполагается, что единичной ступенчатой функцией 1(t) имеет туже размерность, что и физическая величина на входе звена. Если воздействие представляет собой неединичную ступенчатую функцию y(t)=у_уст.×1(t), выходная величина будет равна x(t)= у_уст.h(t).

Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы и т.п. Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) означает, что функция времени x(t) будет существовать только при t³ 0, при t < 0 она обращается в нуль.

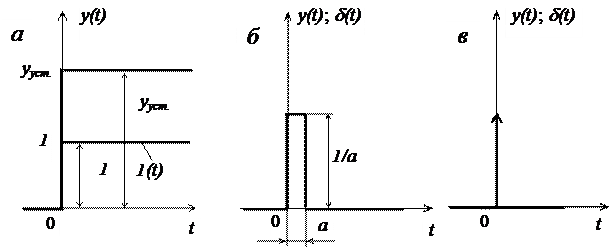Рисунок 1 – Типовые входные воздействия

а – ступенчатые функции – единичная и произвольной величины;

б - единичная импульсная функция конечных параметров;

в - единичная импульсная функция нулевой ширины

2.2.3. Импульсная переходная функцияили весовая функция (функция веса) - w(t)описывает переходной процесс на выходе звена (реакцию звена, системы), возникающий при подаче на его вход единичного импульса при нулевых начальных условиях.

2.2.4. Единичный импульс – дельта-функция d(t)– это математическая идеализация предельно короткого импульсного сигнала, площадь которого равна единице при длительности равной нулю, и высоте равной бесконечности. Дельта-функция представляет собой производную от единичной ступенчатой функции

d(t) = 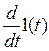= 1¢(t) (3)

или в операционной форме

d(s) = sL[1(t)] = s 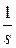=1. (4)

Поэтому

L[w(t)] = W(s) d(s) =W(s),(5)

т.е. изображение импульсной переходной функции равно передаточной функции. Отсюда, для характеристики динамических свойств звена (системы) в равной мере могут быть использованы как передаточная, так и импульсная переходная функция. Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что

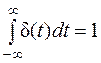. (6)

Формула (6) означает, что площадь под дельта-функцией равна единице. Из (6) также следует, что ее размерность равна [с^-1]. Функции W(s), h(t) и w(t) связаны между собой:

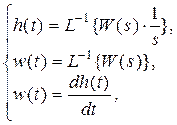(8)

где L^-1{×} – обратное преобразование Лапласа; 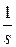– изображение по Лапласу функции 1(t).

Импульсная функция также представляет собой распространенный вид входного воздействия в автоматических системах. Это, например, кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания генератора, отключаемого плавкими предохранителями и т.д.

При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс в системе часто возникает при включениях и изменении задания регулятору.

Для определения временных характеристик единичное скачкообразное постоянное или в виде импульса воздействие принято для того, чтобы однозначно оценивать динамические свойства звена или системы, так как при различной величине воздействий выходная величина даже одной и той же системы будет изменяться по-разному. Кроме того, использование ступенчатого постоянного или импульсного воздействия в виде стандартного входного сигнала имеет также и то преимущество, что действительные, любой формы, возмущающие воздействия на систему можно представить в виде последовательности таких сигналов, например так как показано на рисунке 2.

Рисунок 2 – Представление входного воздействия произвольной формы суммой входных ступенчатых воздействий

При поступлении на вход звена или разомкнутой системы с передаточной функцией W(p) входной величины y(t) = 1(t) на выходе получаем переходную характеристику x = h(t). Входная и выходная величины, преобразованные по Лапласу запишутся следующим образом

Y(p) = L[y(t)] = L[1(t)] = 1/p; (9)

X(p) = L[h(t)] = h(p). (10)

С учетом этих соотношений получим:

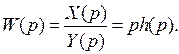(11)

Из выражения (11) следует, что по временной характеристике системы (по переходной функции) можно получить передаточную функцию системы. В свою очередь изображение по Лапласу переходной функции определяется выражением

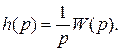(12)

Из выражения (12) с помощью обратного преобразования Лапласа можно определить переходную функцию разомкнутой системы:

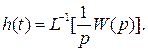(13)

Аналогично переходная функция замкнутой системы имеет вид:

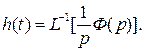(14)

2.3. Апериодическое звено - инерционное звено первого порядка.Звену соответствует дифференциальное уравнение

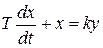. (15)

В операторной форме уравнение имеет вид:

TpX(p) + X(p) = kY(p). (16)

Передаточная функция звена

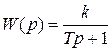. (17)

Определим характер изменения выходной величины X(p) при изменении скачком входной величины y(t) = y_уст.×1(t) (где y_уст. – величина скачка). По таблицам преобразований Лапласа изображение входной величины имеет вид:

Y(p)= L[y(t)] = L[y_уст.×1(t)] = y_уст./p.(18)

По формуле (1) можно определить изображение выходной величины

X(p) = W(p)Y(p). (19)

Тогда с учетом (17) и (18) из (19) получим:

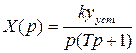(20)

Оригинал функции x(t) через ее изображение находится по таблице преобразований Лапласа после того, как в формуле (20) вынести постоянные величины за знак преобразования Лапласа

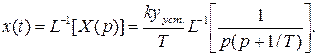(21)

Полагая, что 1/T = а, по таблице преобразований Лапласа можно найти

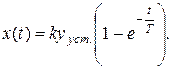(22)

Апериодическими звеньями первого порядка является, например, резервуар с газом, у которого входная величина представляет собой давление p₁ впускным отверстием, а выходная – давление p₂ в резервуаре – рисунок 3а.

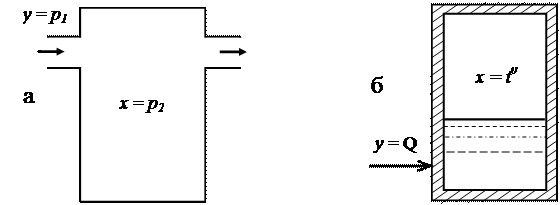
Рисунок 3 – Примеры устройств, работа которых описывается

апериодическими звеньями первого порядка

а – резервуар с газом; б – нагревательная печь

Другим примером может служить нагревательная печь - рисунок 3б, у которой входная величина – количество поступающего в единицу времени тепла Q, а выходная - температура в печи t⁰.

2.3.1. Переходная функция h(t) апериодического звена получается из уравнения (22) при y_уст. = 1 – при подаче на вход звена единичного ступенчатого воздействия 1(t)

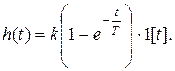(23)

Переходной процесс апериодического звена (22) представлен на рисунке 4.

Графические зависимости переходного процесса имеют вид экспонент. Поэтому время t, необходимое для того, чтобы выходная величина x(t) достигла установившегося значения x(t) = x_уст. = ky_уст. (при единичном входном сигнале y_уст. = 1, а x(t)= x_уст. = k), теоретически бесконечно велико. Величина T имеет размерность времени и называется постоянной времени. Физический смысл постоянной времени заключается в том, что это время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

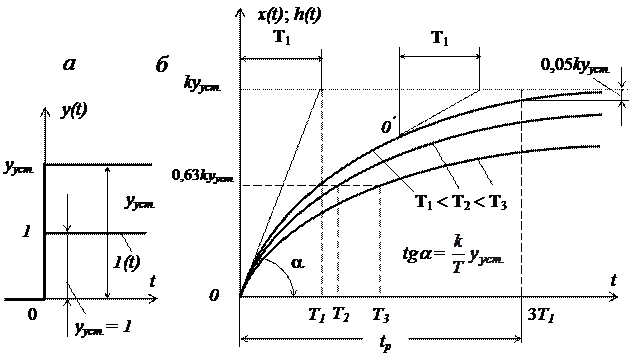
Рисунок 4 - Переходной процесс - переходная функция апериодического звена

а – графики скачкообразного изменения входной величины у апериодического звена (единичного и произвольной величины); б – графики переходной функции апериодического звена - изменения выходной величины при различных значениях постоянной времени

Постоянная времени определяет динамические свойства звена. Чем она больше, тем медленнее протекает переходный процесс в звене, и наоборот. В частности, при T = 0 процесс протекает в звене мгновенно и инерционное звено превращается в безынерционное усилительное звено. При t = T значение выходной величины составляет 63% нового установившегося значения. Постоянная времени апериодического звена геометрически определяется как проекция на ось времени отрезка касательной к экспоненте, заключенного между точкой касания и точкой пересечения касательной с линией установившегося значения выходной величины. Длина этой проекции одинакова для касательных, проведенных в любой точке экспоненты (точки 0 и 0¢). Практически переходной процесс считается закончившимся через промежуток времени t_р = 3T.

2.3.2. Импульсная переходная функция w(t) апериодического звена - реакция апериодического звенана импульсное входное воздействие может быть найдена дифференцированием переходной функции h(t).

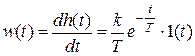. (24)

Вид импульсной переходной функции звенапоказан на рисунке 5.

2.4. Безынерционное (пропорциональное, усилительное) звено.Это звено не только в статике, но и в динамике описывается алгебраическим уравнением

x(t) = ky(t). (25)

Передаточная функция звена равна постоянной величине

W(p) = k. (26)

Примером такого звена является механический редуктор (без учета явлений скручивания и люфта), усилитель, делитель напряжения и т.п. Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не имеет постоянную времени равную нулю. К такому звену сводится одно из реальных звеньев, например, апериодическое, колебательное и др. если можно пренебречь влиянием динамических (переходных) процессов в этом звене (при T =0).

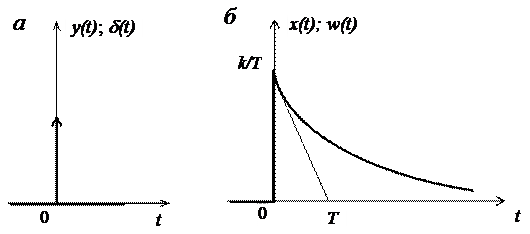Рисунок 5 - Импульсная переходная функция апериодического звена

a – импульсное воздействие d(t) на входе апериодического звена;

б – график импульсной переходной функции апериодического звена

2.4.1. Переходная функция такого звена представляет собой ступенчатую функцию, т.е. при

y(t) = 1(t); (27)

x(t) = h(t) = k×1(t). (28)

Выражение (28) для переходной функции усилительного звена получается из (23) апериодического звена при T = 0, когда инерционное звено превращается в безынерционное. Переходный процесс усилительного звена показан на рисунке 6.

2.4.2. Импульсная переходная функция (функция веса) усилительного звена представляет собой функцию, площадь которой равна k, т.е. при

y(t) = d(t); (29)

x(t) = w(t) = k×d(t). (30)

Из (30) видно, что график импульсной переходной функции усилительного звена совпадает с графиком дельта-ф