Тема: «Интегральное исчисление функции одной переменной»
Тема: «Интегральное исчисление функции одной переменной»
Введение
Интеграл – одно из основных математических понятий, возникшее в связи с отысканием функции по заданной ее производной и вычислением площади криволинейной трапеции. Эти задачи привели к двум видам интеграла: неопределенному и определенному.
Изучение свойств и методов вычисления интеграла составляет задачу интегрального исчисления. Интегральное исчисление тесно связано с дифференциальным исчислением.
Первообразная. Неопределенный интеграл и его основные свойства
Основной задачей дифференциального исчисления является нахождение производной или дифференциала заданной функции.
Основной задачей интегрального исчисления является нахождение функции по заданной ее производной или дифференциалу.
Определение: Функция называется первообразной для данной функции, если ее производная равна данной функции.
Обозначение: 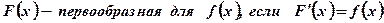 .
.
Вопрос: Является ли функция х2 первообразной для функции 2х?
Ответ: Функция х2 является первообразной для функции 2х, так как 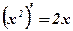 .
.
Вопрос: Какая из двух функций х5+7 или 5х4 является первообразной для другой?
Ответ: Функция х5+7 является первообразной для функции 5х4, так как 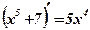 . Функция 5х4 является производной от функции х5+7.
. Функция 5х4 является производной от функции х5+7.
Упражнения:
Какая из двух функций является первообразной для другой?
1) 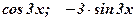 ; ; | 2) 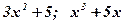 ; ; | 3) 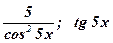 . . |
Дифференциал первообразной
Пусть функция 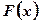 является первообразной для функции
является первообразной для функции 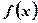 , то есть
, то есть 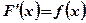 .
.
Воспользуемся определением дифференциала функции для вычисления дифференциала первообразной:
Дифференциалом функции называется произведение производной функции на дифференциал аргумента, то есть 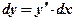 .
.
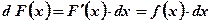
Вывод: Дифференциал первообразной для данной функции равен произведению данной функции на дифференциал аргумента.
Пример: Найти дифференциал первообразной для функции 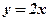 .
.
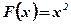 ;
; 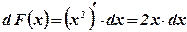 ;
; 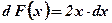 .
.
Задача: Являются ли функции 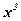 ;
; 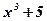 ;
; 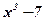 ;
; 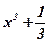 первообразными для функции
первообразными для функции 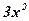 ?
?
Воспользуемся определением первообразной: 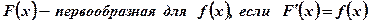 .
.
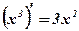 ;
; 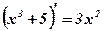 ;
; 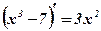 ;
; 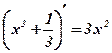 .
.
Ответ: Данные функции являются первообразными для функции 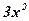 .
.
Вывод: Функция 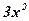 имеет бесконечное множество первообразных, отличающихся друг от друга на постоянную:
имеет бесконечное множество первообразных, отличающихся друг от друга на постоянную: 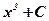 , С – постоянная.
, С – постоянная.
Теорема: Если функция 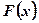 является первообразной для функции
является первообразной для функции 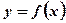 на интервале
на интервале 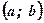 , то множество всех первообразных для функции
, то множество всех первообразных для функции 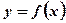 задается формулой
задается формулой 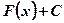 , где С – постоянная.
, где С – постоянная.
Замечание: Операция нахождения всех первообразных 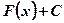 для данной функции
для данной функции 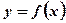 называется интегрированием этой функции. Интегрирование обозначается с помощью знака неопределенного интеграла
называется интегрированием этой функции. Интегрирование обозначается с помощью знака неопределенного интеграла 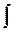 .
.
Определение: Неопределенным интегралом от данной функции называется совокупность ее первообразных: 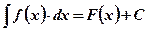 .
.
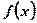 – подынтегральная функция;
– подынтегральная функция; 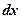 – дифференциал аргумента х;
– дифференциал аргумента х;
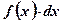 – подынтегральное выражение;С – постоянная интегрирования.
– подынтегральное выражение;С – постоянная интегрирования.
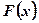 – первообразная для функции
– первообразная для функции 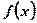 .
.
Пример:
|
|
Замечание:
- Интеграл называется неопределенным, так как результат интегрирования не однозначен.
- Графики всех первообразных
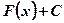 для функции
для функции 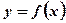 получаются из любого из них параллельным переносом вдоль оси Оу.
получаются из любого из них параллельным переносом вдоль оси Оу. - При нахождении для данной функции первообразной, удовлетворяющей начальным условиям, надо найти значение постоянной интегрирования.
- Дифференцирование (нахождение производной или дифференциала функции) и интегрирование являются взаимно обратными действиями.
Пример:
1) 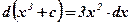 ;
; 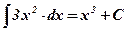 .
.
2) 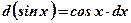 ;
; 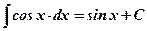 .
.
- Чтобы найти неопределенный интеграл от данной функции, нужно найти одну из ее первообразных и прибавить к ней произвольную постоянную.
Табличные интегралы
1) 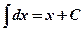 ; 2) ; 2)  , , 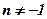 ; 3) ; 3) 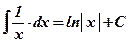 ; 4) ; 4) 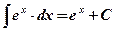 ; 5) ; 5) 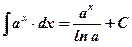 ; 6) ; 6) 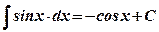 ; 7) ; 7) 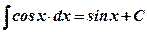 ; ; | 8) 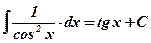 ; 9) ; 9) 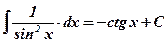 ; 10) ; 10) 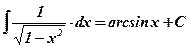 ; 11) ; 11) 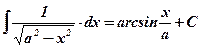 ; 12) ; 12) 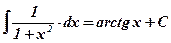 ; 13) ; 13) 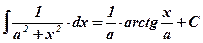 . . |
Методы интегрирования
4)
| х |  |

Ответ:  .
.
Упражнения: Вычислить определённые интегралы:
1)  ; ; | 2)  ; ; | 3)  ; ; |
4)  ; ; | 5)  ; ; | 6)  ; ; |
7)  ; ; | 8)  ; ; | 9)  ; ; |
10)  ; ; | 11)  ; ; | 12)  ; ; |
13)  ; ; | 14)  ; ; | 15)  ; ; |
16)  ; ; | 17)  ; ; | 18)  ; ; |
Ответы:
1)  ; ; | 2)  ; ; | 3)  ; ; | 4) 2; | 5)  ; ; | 6)  ; ; |
7)  ; ; | 8)  ; ; | 9) 1; | 10)  ; ; | 11)  ; ; | 12) 2; |
| 13) 2; | 14)  ; ; | 15)  ; ; | 16)  ; ; | 17)  ; ; | 18)  . . |
Рис. 1. Рис. 2. Рис. 3. Рис. 4.

Рис. 5. Рис. 6. Рис. 7.
Решение:
Рис.1. Фигура не является криволинейной трапецией, так как функция, её ограничивающая принимает отрицательные значения при рассматриваемых значениях аргумента.
Рис.2. Фигура не является криволинейной трапецией, так как она не ограничена справа прямой, параллельной оси ординат.
Рис.3. Фигура не является криволинейной трапецией, так как она не ограничена осью абсцисс.
Рис.4. Фигура является криволинейной трапецией, так как она ограничена осью абсцисс, двумя прямыми, параллельными оси ординат, непрерывной и неотрицательной функцией  при рассматриваемых значениях аргумента.
при рассматриваемых значениях аргумента.
Рис.5. Фигура не является криволинейной трапецией, так как функция, её ограничивающая принимает неотрицательные и отрицательные значения при рассматриваемых значениях аргумента.
Рис.6. Фигура не является криволинейной трапецией, так как функция, её ограничивающая не является непрерывной при рассматриваемых значениях аргумента.
Рис.7. Фигура не является криволинейной трапецией, так как она не ограничена осью абсцисс.
Задача №2. Выразить площади фигур через площади криволинейных трапеций.
 |
Рис. 1. Рис. 2. Рис. 3.

Рис. 4. Рис. 5.
Решение:
- Площадь фигуры BCE (Рис.1.) равна разности площадей криволинейных трапеций ABCD u ABECD:
 .
. - Площадь фигуры ABC (Рис.2.) равна сумме площадей криволинейных трапеций ABD u BCD:
 .
. - Площадь фигуры BCDF (Рис.3.) равна разности площадей криволинейных трапеций ABCDЕ u ABFDE:
 .
. - Площадь фигуры ABCD (Рис.4.) равна разности площадей криволинейных трапеций ABC u ADC:
 .
. - Площадь фигуры ABC (Рис.5.) равна сумме площадей криволинейных трапеций ABD u BCD:
 .
.
Задача №3. Найти концы интервала, на котором построена фигура, ограниченная функциями:
1)  ;
; 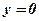 ; 2)
; 2)  ;
;  ; 3)
; 3)  ;
;  .
.
 |
Рис. 1. Рис. 2. Рис. 3.
Решение:
1) Концами интервала a u b, на котором построена данная криволинейная трапеция, являются абсциссы точек пересечения параболы  и оси абсцисс
и оси абсцисс 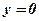 . Решим способом подстановки систему уравнений:
. Решим способом подстановки систему уравнений:
 Û
Û  Û
Û 
 ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;  ;
;
Ответ:  ;
;  .
.
2) Концами интервала a u b, на котором построена данная фигура, являются абсциссы точек пересечения параболы  и прямой
и прямой  . Решим способом подстановки систему уравнений:
. Решим способом подстановки систему уравнений:
 Û
Û  Û
Û 
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;
Ответ:  ;
;  .
.
3) Концами интервала a u b, на котором построена данная фигура, являются абсциссы точек пересечения парабол  и
и  . Решим способом подстановки систему уравнений:
. Решим способом подстановки систему уравнений:
 Û
Û  Û
Û 
 ;
;  ;
;  ;
;  ;
;  ;
;
Ответ:  ;
;  .
.
Упражнения:  Построить фигуру, ограниченную функциями
Построить фигуру, ограниченную функциями  ,
, 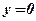 ,
, 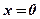 ,
, 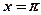 . Является ли фигура криволинейной трапецией? Найти концы интервала, на котором построена фигура.
. Является ли фигура криволинейной трапецией? Найти концы интервала, на котором построена фигура.
Построим криволинейную трапецию Р0М0МР, ограниченную функцией 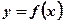 , положительной и возрастающей при рассматриваемых значениях аргумента
, положительной и возрастающей при рассматриваемых значениях аргумента  .
.
От чего зависит площадь криволинейной трапеции Р0М0МР?
1. Площадь криволинейной трапеции Р0М0МР зависит от длины отрезка  , на котором она построена: чем больше длина отрезка
, на котором она построена: чем больше длина отрезка  , тем больше площадь криволинейной трапеции Р0М0МР .
, тем больше площадь криволинейной трапеции Р0М0МР .
2. Площадь криволинейной трапеции Р0М0МР зависит от вида ограничивающей её функции 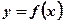 .
.
Вывод: Площадь криволинейной трапеции, ограниченной непрерывной и неотрицательной функцией 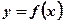 на отрезке
на отрезке 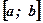 оси абсцисс равна определённому интегралу в пределах от а до b от функции
оси абсцисс равна определённому интегралу в пределах от а до b от функции 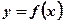 .
. 
 Вывод: Геометрический смысл определённого интеграла состоит в том, что определённый интеграл в пределах от а до b от непрерывной и неотрицательной функции
Вывод: Геометрический смысл определённого интеграла состоит в том, что определённый интеграл в пределах от а до b от непрерывной и неотрицательной функции 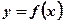 равен площади криволинейной трапеции, ограниченной функцией
равен площади криволинейной трапеции, ограниченной функцией 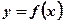 на отрезке
на отрезке 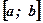 оси абсцисс.
оси абсцисс. 
Пример:
- Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией  . Сделать чертёж.
. Сделать чертёж.
Решение:
Воспользуемся формулой площади криволинейной трапеции: 
 .
.
Ответ: 
- Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией  . Сделать чертёж.
. Сделать чертёж.
 Решение:
Решение:
 ;
; 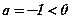 - ветви направлены вниз;
- ветви направлены вниз;
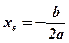 ;
;  ;
;
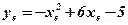 ;
;  ;
;
 - вершина параболы;
- вершина параболы;
 - ось симметрии параболы;
- ось симметрии параболы;
| х | ||||
| у | - 5 |
Концы интервала, на котором построена данная криволинейная трапеция, являются абсциссами точек пересечения параболы  и оси абсцисс
и оси абсцисс 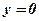 . Решим способом подстановки систему уравнений:
. Решим способом подстановки систему уравнений:
 Û
Û 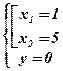 Û
Û 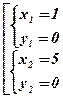
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;
Воспользуемся формулой площади криволинейной трапеции:  .
.

Ответ: 
Упражнения:
- Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 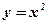 . Сделать чертёж.
. Сделать чертёж. - Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией  . Сделать чертёж.
. Сделать чертёж. - Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией  . Сделать чертёж.
. Сделать чертёж. - Вычислить площадь криволинейной трапеции, построенной на отрезке
 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией  . Сделать чертёж.
. Сделать чертёж. - Вычислить:
 .
.
Рис. 1. Рис. 2.
Решение:
1) Фигура не является криволинейной трапецией, так как функция, её ограничивающая, принимает и отрицательные и неотрицательные значения при рассматриваемых значениях аргумента. 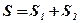 .
.
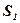 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 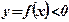 при
при 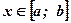 :
: 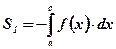 .
.
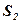 - площадь кр. тр., ограниченной функцией
- площадь кр. тр., ограниченной функцией 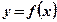 при
при 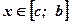 :
: 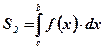 .
.
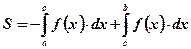
2) Фигура не является криволинейной трапецией, так как функция, её ограничивающая, принимает и отрицательные и неотрицательные значения при рассматриваемых значениях аргумента. 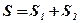 .
.
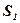 - площадь кр. тр., ограниченной функцией
- площадь кр. тр., ограниченной функцией 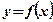 при
при 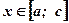 :
: 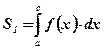 .
.
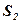 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 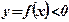 при
при 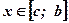 :
: 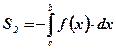 .
.
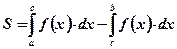
Вывод: Площадь фигуры, построенной на отрезке 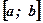 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 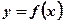 , пересекающей ось абсцисс внутри рассматриваемого отрезка, вычисляется по формуле:
, пересекающей ось абсцисс внутри рассматриваемого отрезка, вычисляется по формуле: 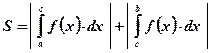 .
.
Пример: Вычислить площадь фигуры, ограниченной функциями: 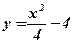 ,
, 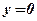 ,
, 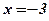 ,
, 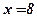 .
.
Решение: 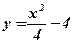 ;
; 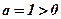 - ветви направлены вверх;
- ветви направлены вверх;
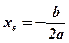 ;
; 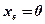 ;
; 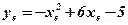 ;
; 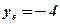 ;
;
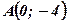 - вершина параболы;
- вершина параболы;
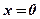 - ось симметрии параболы;
- ось симметрии параболы;
| х |  8 8 | ||||
| у | - 4 | - 3 |
Фигура не является криволинейной трапецией, так как функция 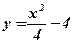 принимает отрицательные значения при
принимает отрицательные значения при 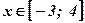 и неотрицательные значения при
и неотрицательные значения при 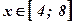 .
. 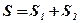 .
.
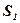 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 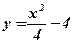 при
при 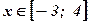 , вычисляется по формуле
, вычисляется по формуле 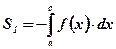 ;
;
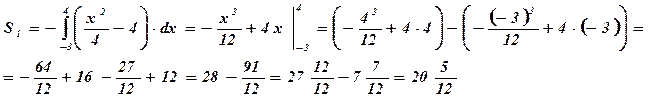
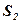 - площадь кр. тр., ограниченной функцией
- площадь кр. тр., ограниченной функцией 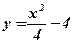 при
при 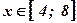 , вычисляется по формуле
, вычисляется по формуле 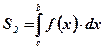 ;
;
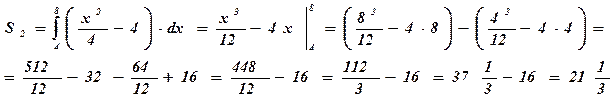
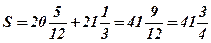
 Ответ:
Ответ: 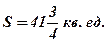
Задача №3: Определить площадь фигуры, построенной на отрезке 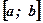 оси абсцисс и ограниченной функциями:
оси абсцисс и ограниченной функциями: 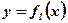 при
при 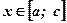 и
и 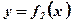 при
при 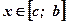 ,
, 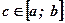 .
.
Решение:
Фигура не является криволинейной трапецией, так как ограничена двумя функциями. Прямой, проходящей через точку пересечения функций 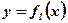 и
и 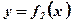 и параллельной оси ординат, фигура разбивается на части
и параллельной оси ординат, фигура разбивается на части 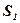 и
и 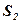 , являющиеся криволинейными трапециями.
, являющиеся криволинейными трапециями. 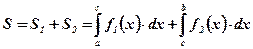 .
.
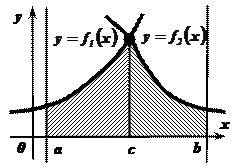
Задача №4: Определить площадь фигуры, ограниченной функциями 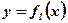 и
и 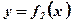 , удовлетворяющими условию
, удовлетворяющими условию 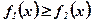 при рассматриваемых значениях аргумента
при рассматриваемых значениях аргумента 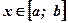 .
.
Решение:
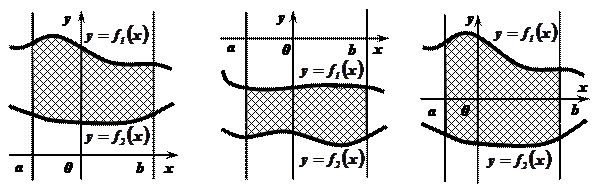 |
Рис. 1. Рис. 2. Рис. 3.
Тема: «Интегральное исчисление функции одной переменной»
Введение
Интеграл – одно из основных математических понятий, возникшее в связи с отысканием функции по заданной ее производной и вычислением площади криволинейной трапеции. Эти задачи привели к двум видам интеграла: неопределенному и определенному.
Изучение свойств и методов вычисления интеграла составляет задачу интегрального исчисления. Интегральное исчисление тесно связано с дифференциальным исчислением.

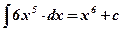 ;
;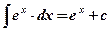 ;
;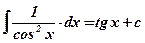 ;
;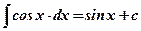 .
.