Способы решения логарифмических уравнений.

По определению логарифма.

Так решаются простейшие уравнения вида .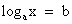

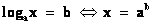
Решить уравнение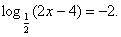

(По определению логарифма)

Решение. 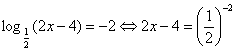, Отсюда 2х – 4 = 4; х = 4.

Ответ: 4.

2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).

пример 2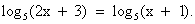

Решение 1. ОДЗ: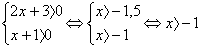

Потенцируем исходное уравнение , получим уравнение 2x + 3 = х + 1. Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.

Можно решить это уравнение иначе – переходом к равносильной системе:

Уравнение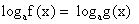

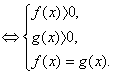
(Система содержит избыточное условие – одно из неравенств можно не рассматривать).

равносильно системе:

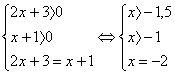
Эта система решений не имеет.

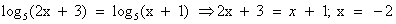. Сделаем проверку: 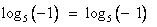неверно, так как не имеет смысла.

Ответ: корней нет.

3. Введение новой переменной.

.

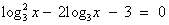Решение. ОДЗ: х > 0.

Пусть 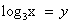, тогда уравнение примет вид: 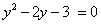. Дискриминант D > 0. Корни по теореме Виета: .

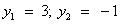Вернемся к замене: 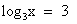или .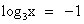

Решив простейшие логарифмические уравнения, получим:

; .

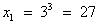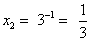Ответ: 27;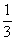

Логарифмирование обеих частей уравнения.

Решить уравнение: .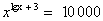

Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:

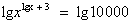. Применим свойство логарифма степени:

(lgx + 3) lgx =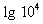

(lgx + 3) lgx = 4

Пусть lgx = y, тогда (у + 3)у = 4

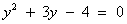, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.

Вернемся к замене, получим: lgx = -4, 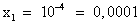; lgx = 1, .

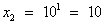Ответ: 0,0001; 10.

Приведение к одному основанию.

Решите уравнение: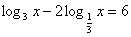

Решение: ОДЗ: х>0. Перейдем к основанию 3.

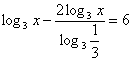или ; .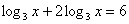

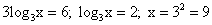Ответ: 9.

Функционально-графический метод.

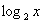= 3 – x.

Есть способ, позволяющий не строить графики. Он заключается в следующем:

Если одна из функций у = f(x) возрастает, а другаяy = g(x)убывает на промежутке Х, то уравнениеf(x)= g(x)имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

В нашем случае функция 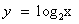возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 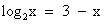имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .

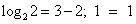Ответ: 2

Логарифмические неравенства

Логарифмическим неравенством называется неравенство, в котором неизвестная величина стоит под знаком логарифма.

Теорема 2. Если f(x) > 0 и g(x) > 0, то:
при a > 1 логарифмическое неравенство log _a f(x) > log _a g(x) равносильно неравенству того же смысла: f(x) > g(x);
при 0 < a < 1 логарифмическое неравенство log _a f(x) > log _a g(x) равносильно неравенству противоположного смысла: f(x) < g(x).

Пример 1. Решите неравенство:

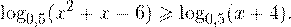
Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:

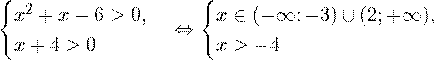
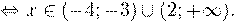
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:

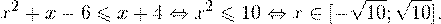
Окончательно, с учетом области допустимых значений получаем ответ: