Способы решения показательных неравенств

Показательная функция в зависимости от основания может быть возрастающей (а>1) или убывающей (а<1)

Примеры.

Неравенства, сводящиеся к простейшим. Решаются приведением обеих частей неравенства к степени с одинаковым основанием.

а)2^x2> 2 ^x+2.

Решение:

2^x2> 2 ^x+2;
х² > х+2, т.к.функция y =2^t возрастает,
х² – х–2 > 0;
x < – 1; x > 2.

Ответ: .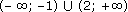

б) .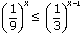

Решение:

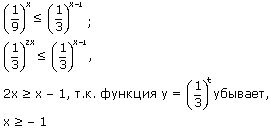
Ответ: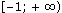

Неравенства, решаемые с помощью вынесения за скобки общего множителя.

8 × 2^{х – 1} – 2^х > 48

Решение: 2^х–1 (8 – 2) > 48,

2^х–1 > 8,

2^х–1 > 2³,

х – 1 > 3, т.к. функция y = 2^tвозрастает,

х > 4.

Ответ: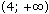

Неравенства, решаемые с помощью замены переменной.

2^х + 2^{3 – х} < 9

Решение:

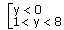
а) 2^х< 0. Неравенство решений не имеет, т.к. 2^х > 0.

б) 1 < 2^х< 8; 2⁰ < 2^х < 2³; 0 < x < 3, т.к. функция y = 2^х возрастает.

Ответ: (0; 3).

Логарифмические уравнения и их функции

Функцию вида y = log_a x, a > 0, a ≠ 1 называют логарифмической функцией.

Графиком логарифмической функции является логарифмическая кривая:

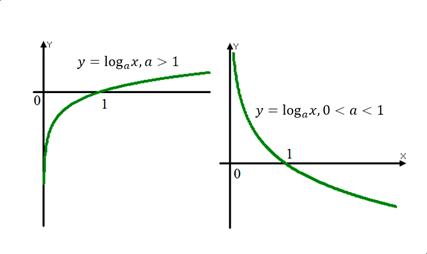
Свойства	a > 1	0 < a < 1
Область определения	D(f) = (0; +∞)	D(f) = (0; +∞)
Область значений	E(f) = (-∞; +∞)	E(f) = (-∞; +∞)
Монотонность	Возрастает на (0; +∞)	Убывает на (0; +∞)
Непрерывность	Непрерывная	Непрерывная
Выпуклость	Выпуклая вверх	Выпуклая вниз

Свойства логарифмов

• Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

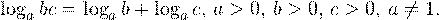
• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:

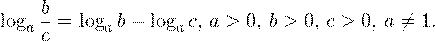
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:

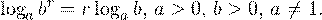
• Равенство log _a t = log _a s, где a > 0, a ≠ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):

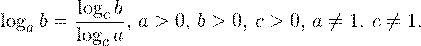
Теорема 1. Если f(x) > 0 и g(x) > 0, то логарифмическое уравнение log _a f(x) = log _a g(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

Пример 1. Решите уравнение:

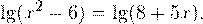
Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:

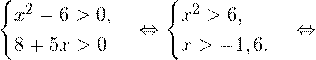
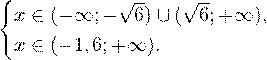
С учетом того, что

получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:

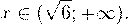
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:

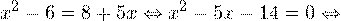
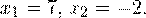
В область допустимых значений входит только первый корень.

Ответ: x = 7.

Пример 2. Решите уравнение:

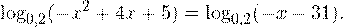
Решение. Область допустимых значений уравнения определяется системой неравенств:

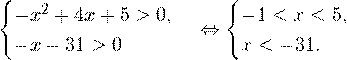
Эти два условия противоречат друг другу, то есть нет такого значения х ,при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет.

Ответ: корней нет.