По теории вероятностей и математической статистике
СПИСОК ВОПРОСОВ к ЭКЗАМЕНУ
По теории вероятностей и математической статистике
Раздел 1. События и их вероятности
Пространство элементарных исходов. Испытания, исходы, определение события. Операции над событиями: объединение, пересечение, дополнение одного события до другого, противоположное событие. Достоверные, невозможные и противоположные события. Диаграммы Эйлера-Венна.
2. Классическое и статистическое определения вероятности. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Формулы комбинаторики.
Теорема о перемножении шансов. Урновые схемы: выбор с возвращением и без, с учетом порядка и без. Число возможных результатов в каждой из схем выбора. Урновые схемы, удовлетворяющие и не удовлетворяющие классическому определению вероятности. Гипергеометрическое распределение.
Геометрическая вероятность. Задача о встрече.
Геометрическая вероятность
Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω: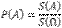 
. Если для точки, брошенной в Ω выполняется условие геометрического определения вероятности, то говорят, что точка равномерно распределена в области Ω.
Задача о встрече.
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Решение:сначала выясняем длительность временного промежутка, на котором может состояться встреча. В данном случае, как уже отмечено выше, это полтора часа или 90 минут. При этом здесь не имеют особого значения фактические временные рамки – погрузка автомобилей, может состояться, например, утром с 8.30 до 10.00, и решение будет точно таким же.
Вычисления допустимо проводить как в долях часа, так и в минутах. На мой взгляд, в большинстве случаев удобнее работать с минутами – меньше путаницы.
На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц; при этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.
Общему множеству исходов будет соответствовать площадь данного квадрата: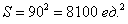 
Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.
 |
Далее по оси
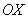от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси 
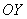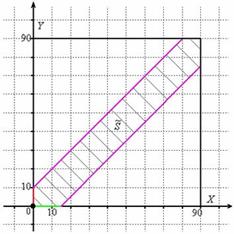
– время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь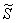 
заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще найти площади двух прямоугольных треугольников с помощью формулы 
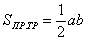, где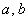 
– длины катетов. Обратите внимание, что в общем случае эти треугольники не равны. У нас: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Таким образом, суммарная площадь треугольников составляет:
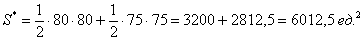
И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:
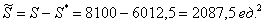
По геометрическому определению:
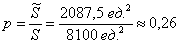– вероятность того, что одной машине придется ждать окончания погрузки другой.
Аксиоматическое определение вероятности: определение и свойства алгебры и s-алгебры событий. Примеры алгебр и s-алгебр (в т. ч. борелевская s-алгебра на прямой). Определение меры. Мера Лебега. Определение вероятностной меры. Свойства вероятности. Вероятность объединения n событий.
Теорема сложения вероятностей для совместных событий. Полная группа событий. Формула полной вероятности. Формула Бейеса. Примеры использования этих формул.
Определение случайной величины. Примеры отображений, являющихся и не являющихся случайными величинами.
Числовые характеристики дискретной случайной величины. Определения моментов. Математическое ожидание и его свойства. Определение и свойства дисперсии. Среднеквадратичное отклонение.
Примеры абсолютно непрерывных распределений: равномерное, показательное, нормальное распределение.
СПИСОК ВОПРОСОВ к ЭКЗАМЕНУ
по теории вероятностей и математической статистике