Совместное распределение нескольких случайных величин. Многомерный нормальный закон

Пусть с испытанием связаны n случайных величин x₁, x₂,….,ξ_n. Укажем кратко, как введенные в этой главе понятия переносятся на этот случай.

1. Совместной функцией распределения случайных величин x₁, x₂,….,ξ_n называется функция

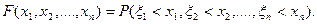
Совместной плотностью вероятности случайных величин x₁, x₂,….,ξ_n называется функция

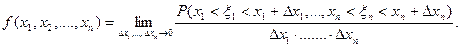Имеет место равенство

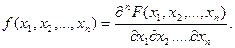
2. Обозначим а_i, σ_j математическое ожидание и СКО случайной величины ξ_i, к_ij – ковариацию случайных величин ξ_i, ξ_j:

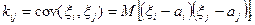
Матрица

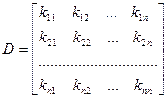
называется дисперсионной матрицей случайных величин x₁, x₂,….,ξ_n. Отметим следующие свойства матрицы D.

1⁰. Элементы главной диагонали матрицы D – дисперсии случайных величин x₁, x₂,….,ξ_n:

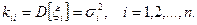
2⁰. Матрица D симметрическая: k_ij=k_ji.

3⁰. Собственные числа матрицы D неотрицательны.

Свойства 1⁰, 2⁰ очевидны. Предлагаем читателю проверить свойство 3⁰ для частного случая n=2. В этом случае матрица D имеет вид

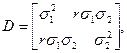(28)

где r – коэффициент корреляции случайных величин x₁, x₂.

3. В §3 этой главы было введено понятие совместного нормального распределения случайных величин x₁, x₂ – см.формулу (25). Это понятие обобщается следующим образом. Говорят, что случайные величины x₁, x₂,….,ξ_n имеют совместное нормальное распределение, если совместная плотность вероятности дается формулой

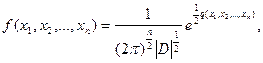
где 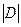- определитель дисперсионной матрицы D,

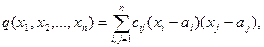
с_ij – элементы матрицы C=D^-1.

Нетрудно проверить, что в частном случае n=2 это определение совпадает с определением (25); для этого нужно воспользоваться формулой (28) для матрицы D и формулой обращения матрицы второго порядка с отличным от нуля определителем:

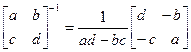
(предлагаем читателю выполнить проверку самостоятельно).

Справедливы утверждения: если x₁, x₂,….,ξ_n имеют совместное нормальное распределение, то каждая из них отдельно также нормальна; если каждая ξ_i нормальна и при этом x₁, x₂,….,ξ_n независимы, то их совместное распределение также нормально, и имеет место формула

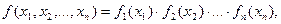
где f_i(x) – плотность вероятности ξ_i. В общей ситуации из нормальности каждой отдельно ξ_i не вытекает нормальность совместного распределения.

Понятие совместного нормального распределения играет важную роль в приложениях теории вероятностей.

Глава 5. Закон больших чисел. Предельные теоремы

Под законом больших чисел понимают закономерности в массовых случайных явлениях, когда взаимодействие большого числа случайных факторов приводит к неслучайному результату. Пример закономерности такого типа приведен во введении: доля наступления случайного события в длинной серии независимых одинаковых испытаний практически неслучайна. Другой замечательный пример: оказывается, в ряде случаев закон распределения суммы большого числа случайных слагаемых не зависит от законов распределения слагаемых и может быть предсказан! Назначение предельных теорем теории вероятностей: дать строгие формулировки и обоснования различных форм закона больших чисел. В этой главе мы кратко рассмотрим результаты такого типа.