Закон распределения случайной точки непрерывного типа на плоскости

В непрерывном случае совместное распределение случайных величин x₁, x₂ не может быть задано (как и в случае одной непрерывной случайной величины x) таблицей, так как в этом случае вероятности отдельных реализаций случайной точки (x₁, x₂) равны нулю.

Совместное распределение задается, как и в случае одной случайной величины, двумя способами: с помощью функции распределения F(х,у) и плотности вероятности f(х,у).

Функция распределения случайной точки (x₁, x₂) определяется равенством

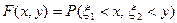
Плотность вероятности случайной точки (x₁, x₂) определяется равенством

y

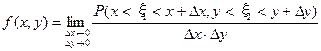
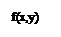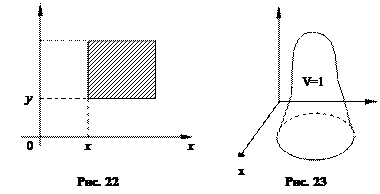
Другими словами, плотность вероятности случайной точки (x₁, x₂) в точке (х,у) есть предел отношения вероятности попадания в заштрихованный прямоугольник (рис.22) к площади этого прямоугольника при условии, что прямоугольник стягивается к точке (х,у). Нестрого говоря, плотность вероятности случайной точки – вероятность попадания на участок с площадью единица.

Перечислим без доказательства основные свойства плотности вероятности f(х,у) (первые 4 из них аналогичны свойствам плотности вероятности f(х) одной непрерывной случайной величины, 5-е и 6-е указывают связь закона распределения случайной точки (x₁, x₂) с законами распределения ее координат).

1⁰. f (x, y) ≥ 0;

2⁰. Вероятность попадания случайной точки в любую область D на плоскости дается формулой

P ((x₁, x₂) Î D) = .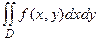

3⁰. Объем фигуры, заключенной между плоскостью хОу и графиком плотности (рис.23), равен единице: V = 1.

4⁰. .

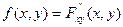5⁰. Законы распределения координат случайной точки (x₁,x₂) восстанавливаются по совместному закону распределения по формулам

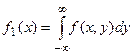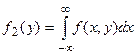, (20)

6⁰. Совместный закон распределения восстанав-ливается по законам распределения координат только в случае, когда x₁, x₂ независимы. В этом случае верна формула

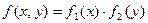(21)

Последнее равенство является необходимым и достаточным условием независимости x₁, x₂.

Отметим, что функция распределения F(х,у) имеет смысл и в дискретном случае. В непрерывном случае при изучении совместных свойств случайных величин, как правило, удобнее пользоваться плотностью вероятности f(х,у).

Пример. Случайная точка (x₁, x₂) равномерно распреде­лена в треугольнике со сторонами: х = 0, y = 0, x + y = 3.

Найти: совместную плотность f(x,y), плотности вероятности f₁(x), f₂(y) слу­чайных величин x₁, x₂. Проверить зависимы x₁ и x₂ или нет.

Решение. Так как случайная точка (x₁, x₂) равномерно

распределена в треугольнике AOB (рис. 24), то f (x, y) = const для точек из D_АОВ. Тогда, используя свойство 3⁰, имеем

S_осн · h = 1, следовательно

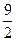· h = 1, откуда h = 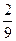и

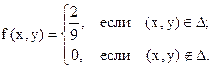
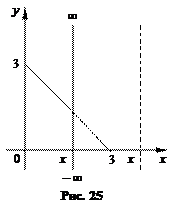По формулам (20) находим:

.

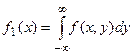Если х Ï [0, 3], то f (x, y)=0 (рис.25) и, следовательно, f₁ (x) = 0.

Если хÎ [0,3], то f (x, y) = 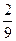, откуда .

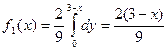Окончательно,

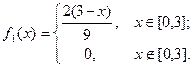
аналогично,

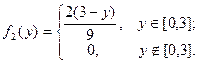
Так как f₁(x) · f₂ (y) ¹ const, то равенство (21) не выполняется, следовательно x₁, x₂ статистически зависимы.

Ковариация двух случайных величин.

Коэффициент корреляции

1. Пусть с испытанием связаны случайные величины x₁,x₂ с числовыми характеристиками (а₁,s₁), (а₂,s₂). Ковариацией случайных величин x₁, x₂ называется число

cov (x₁, x₂) = M [(x₁ – a₁) (x₂ – a₂)].

Из определения следует: в дискретном случае

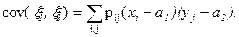(22)

в непрерывном случае

cov (x₁, x₂) = 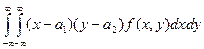. (23)

Укажем основные свойства ковариации.

1⁰. cov (x, x) = d_x.

2⁰. cov (x₁, x₂) = M [x₁, x₂]-а₁а₂.

3⁰. Если x₁, x₂ независимы, то cov (x₁, x₂)=0.

4⁰. |cov (x₁, x₂) | ≤ s₁· s₂ .

5⁰. Если в 4⁰ имеет место равенство: |cov(x₁,x₂)| =s₁· s₂, то между x₁,x₂ имеется линейная функциональная связь:

Аx₁ + Вx₂ + С = 0 при некоторых А,В,С.

Геометрически это означает, что реализации случайной точки (x₁, x₂) с достоверностью ложатся на прямую Ах + By + С = 0.

Докажем свойства 1⁰ – 4⁰.

1. cov (x, x)= M [(x – a) (x – a)]= d_x.

2. cov (x₁, x₂) = M [(x₁x₂– a₁x₂ – a₂x₁ + a₁a₂] =M [x₁·x₂] – a₁M [x₂] – a₂M [x₁] + a­₁ · a₂ = M [x₁ · x₂] – a­₁ · a₂ – a­₂· a₁ + a­₁ · a₂ = M [x₁ · x₂] – a₁ · a₂.

3. Из независимости x₁,x₂ следует независимость случайных величин x₁–a₁, x₂–a₂. Так как математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, то имеем

cov (x₁, x₂) = M (x₁ – a₁) M (x₂ – a₂)=(M[x₁]– a₁) (M[x₂]– a₂)= =(a₁ – a₁)( a₂ – a₂)=0.

4. Доказательство этого свойства проведем для непрерывного случая. Представим указанную в начале параграфа интегральную формулу для ковариации в виде

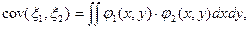
где обозначено

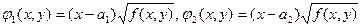
(для удобства записи пределы интегрирования опущены). Воспользуемся известным фактом математического анализа-неравенством Буняковского: для любых непрерывных φ₁, φ₂ и любой области D

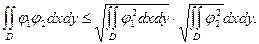
Отсюда следует:

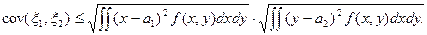
Имеем:

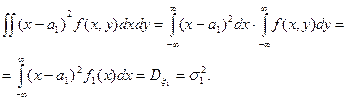
В этом вычислении учтено свойство 5⁰ плотности вероятности f(х,у) и определение дисперсии непрерывной случайной величины. Аналогично найдем

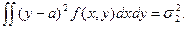
Таким образом

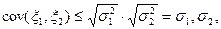
что и требовалось.

2. На практике при изучении совместных свойств случайных величин, как правило, пользуются нормированной ковариацией или коэффициентом корреляции:

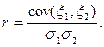(24)

Из свойств ковариации вытекают следующие свойства коэффициента корреляции.

1⁰. -1 ≤ r ≤ 1.

2⁰. Если r = ± 1, то между x₁, x₂ имеется линейная функциональная связь (рис.26). Уравнение прямой вычисляется по параметрам (а₁, а₂, σ₁, σ₂, r).

3⁰. Если x₁, x₂ независимы, то r = 0.

Замечание 1. Из 1⁰-3⁰ следует, что коэффициент корреляции (и, соответственно, ковариации) является некой мерой связи между x₁, x₂. Более подробные рассмотрения показывают следующее. Если ׀ r׀ » 1, то связь между x₁, x₂ близка к линейной функциональной: реализации случайной точки (x₁,x₂) с практической достоверностью ложатся вблизи заранее прогнозируемой прямой Ах + By + С = 0. Если r » 0, то либо x₁, x₂ независимы, либо связь между ними имеется, но далека от линейной связи.

Помнить: коэффициент корреляции является мерой линейной связи между случайными величинами.

Замечание 2. В силу свойства 3⁰ из независимости случайных величин x₁,x₂ следует r=0. Обратное утверждение неверно: имеются примеры, когда r=0 и при этом x₁, x₂ зависимы. Укажем важный частный случай, когда из r = 0 следует независимость x₁, x₂. Будем говорить, что случайные величины x₁,x₂ имеют совместное нормальное распределение с параметрами (а₁, σ₁, а₂, σ₂, r), если плотность вероятности случайной точки (x₁, x₂) дается формулой

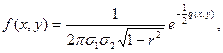(25)

где

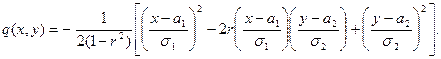Можно показать, что а₁, а₂ – математические ожидания, σ₁, σ₂ – СКО случайных величин x₁, x₂, r- коэффициент корреляции.

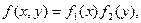(26)

где

,

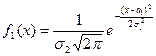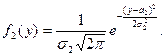
Нетрудно показать, используя свойство 5⁰ плотности вероятности f(x,y), что f₁(x), f₂(y) – плотности вероятности случайных величин x₁, x₂; поэтому в силу свойства 6⁰ f(x,y) x₁, x₂ независимы.

Помнить: в нормальном случае коэффициент корреляции является точной мерой связи между x₁, x₂.

Замечание 3. Числа (а₁, σ₁, а₂, σ₂, r) называются числовыми характеристиками случайной точки (x₁, x₂). Пары (а₁, σ₁), (а₂, σ₂) характеризуют отдельно x₁, x₂; r является мерой связи между x₁, x₂. В непрерывном случае параметр r вычисляется по формулам (23), (24), остальные параметры – по формулам

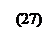
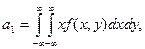
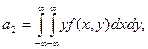
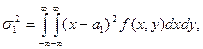
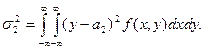
Пример 1. Найти числовые характеристики случайной точки (x₁, x₂) в ситуации примера на стр.57.

Решение. Имеем

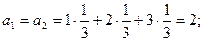
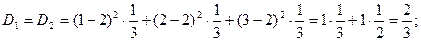s₁ = s₂ = .

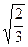Коэффициент корреляции найдем по формулам (22), (24) с учетом свойства 2⁰ для ковариации. Имеем

M [x₁ · x₂] = =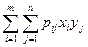

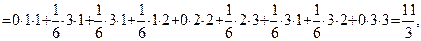откуда

.

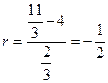Пример 2. Найти числовые характеристики случайной точки (x₁, x₂) в ситуации примера на стр. 60.

Решение. Имеем

а₁ = а₂ = 1, D₁ = D₂ = 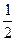, s₁ = s₂ = .

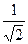Коэффициент корреляции найдем по формулам (23), (24)

cov (x₁, x₂) =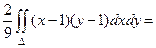

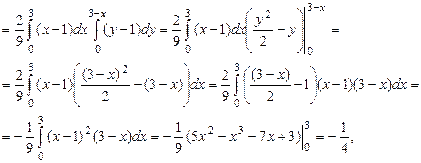откуда

.
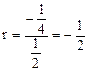