Теоремы сложения и умножения вероятностей

Теорема 1. Пусть с испытанием связаны события А, В. Справедлива формула:

Р (А + В) = Р (А) + Р (В) – Р (А · В). (5)

Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.

Доказательство. Проведем доказательство в рамках схемы геометрической вероятности.

Испытание: берут наугад точку в области D равновозможным образом (рис. 4).

Событие А: попадание в область d₁;

Событие В: попадание в область d₂.

р (А + В) = Р (попадание в заштрихованную область) =

=	благоприятная площадь	=	пл. d1 + пл. d2 –пл. d3	=
вся возможная площадь	площадь D
=	пл.d1	+	пл.d2	–	пл.d3	= Р(А) + Р (В) – Р (АВ),
пл.D	пл.D	пл.D

что и требовалось доказать.

Замечание 1. События А, В называются несовместными, если они не могут произойти одновременно при данном испытании. Для несовместных событий справедлива формула

Р (А + В) = Р (А) + Р (В). (6)

Вероятность суммы несовместных событий равна сумме вероятностей этих событий.

В самом деле, по теореме сложения имеем:

.

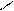
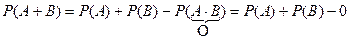Замечание 2. Справедлива формула:

Р(А) = 1 – Р ( ).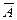

Вероятность наступления события равна единице минус веро­ятность ненаступления события. В самом деле:

;

.

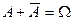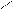
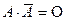Откуда имеем:

,

,

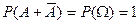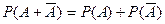следовательно,

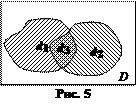
Р(А) + Р ( 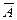) = 1, то есть Р(А) = 1 – Р ( ).

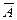Условная вероятность. Теорема умножения вероятностей

Пусть с испытанием связаны события А,В. Запись Р(В/А) означает: вероятность события В при условии, что событие А наступило.

Поясним на примере.

Испытание: берут наугад точку в области D равновозможным образом.

Событие А: попадание в область d₁;

Событие В: попадание в область d₂.

Тогда, имеем (рис.5):

Р(В)= 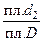,	Р(В/А) =	благоприятная площадь	=	пл. d3
вся возможная площадь	пл. d1	.

Вероятность Р(В/А) называется условной вероятностью.

Теорема 2. Справедлива формула

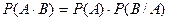. (7)

Вероятность произведения двух событий равна вероятности одного из них, умноженного на вероятность другого при условии, что первое наступило.

Доказательство. Доказательство проведем в рамках схемы геометрической вероятности (рис. 5).

.

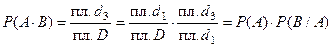Замечание. 1. Будем говорить, что событие В не зависит от события А, если выполняется равенство Р(В/А) = Р(В), в этом случае

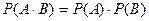. (8)

Вероятность произведения независимых событий равна произведению вероятностей этих событий.

Доказать самостоятельно:

если событие В не зависит от события А, то событие А не зависит от В.

2. .

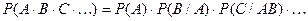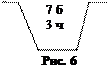Пример. В урне содержится 7 белых и 3 черных шара (рис. 6).

Испытание: из урны берут наугад два шара равновозможным образом.

Найти вероятность того, что они:

а) оба белые (Р(бб) – ?);

б) оба черные (Р (чч) – ?);

в) одного цвета;

г) разного цвета.

Решение.

I способ. По определению вероятности (1) (гл.1§1) и по формуле (2) имеем:

а) Р(бб) ;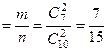

б) Р(чч) .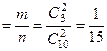

II способ. По формулам (6) и (7) имеем:

а) Р(бб) = Р (1^й белый и 2^й белый) = Р(1^й белый) ·Р (2^й б/ 1^й б) =

.

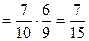б) Р(чч) = Р (1^й черный и 2^й черный) = Р(1^й ч) ·Р (2^й ч/ 1^й ч) =

.

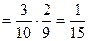в) Р(одного цвета) =Р (1^й б и 2^й б или 1^й ч и 2^й ч) = Р(бб + чч) =

= Р(бб) + Р (чч) = = .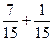

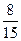г) I способ.

Р (разного цвета) = Р (б·ч + ч·б) = Р (б·ч) + Р(ч·б) =

.

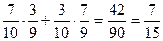II способ.

Р (разного цвета) = 1 – Р (одного цвета) = 1 – 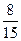= .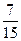