Предмет теории вероятностей.. 5

Введение. 5

Предмет теории вероятностей.. 5

Краткий исторический очерк.. 7

Глава 1. Основные понятия и правила теории вероятностей.. 13

Классическое определение вероятности.. 13

Элементы комбинаторики.. 15

Действия над событиями.. 18

Теоремы сложения и умножения вероятностей.. 20

Формула полной вероятности. Формула Байеса. 24

Схема с повторением испытаний (схема Бернулли) 26

Глава 2. Случайные величины.. 30

Дискретные и непрерывные случайные величины.. 30

Закон распределения дискретной случайной величины.. 32

Математическое ожидание дискретной случайной величины.. 33

Дисперсия дискретной случайной величины.. 36

Закон распределения и числовые характеристики непрерывной случайной величины 38

Глава 3. Основные законы распределения. 45

Биномиальный закон.. 45

Равномерный закон.. 46

Закон Пуассона. 47

Показательный закон.. 49

Нормальный закон.. 53

Глава 4. Совместные распределения случайных величин.. 55

Закон распределения случайной точки дискретного типа на плоскости 55

Закон распределения случайной точки непрерывного типа на плоскости 57

Ковариация двух случайных величин. 60

Коэффициент корреляции.. 60

Совместное распределение нескольких случайных величин. Многомерный нормальный закон 66

Глава 5. Закон больших чисел. Предельные теоремы.. 68

Закон больших чисел в форме Чебышева. 68

Теорема Бернулли.. 72

Центральная предельная теорема. 74

Глава 6. Элементы математической статистики.. 77

Предмет математической статистики.. 77

Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот 78

Выборочная функция распределения. 80

§ 4. Выборочные оценки параметров случайной величины. Основные требования к оценкам 81

Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации 82

Два распределения, связанные с нормальным законом.. 84

Квантиль распределения. 86

Доверительные интервалы для математического ожидания и дисперсии 86

Общая схема проверки гипотез по данным опыта. 88

Проверка гипотезы о законе распределения случайной величины по данным опыта 89

Ошибки первого и второго рода. Мощность критерия. 91

Метод наименьших квадратов (МНК) 92

Дополнения. 94

I. Образцы решения типовых задач. 94

II. Задачи для самостоятельного решения. 118

III. Задания для контрольной работы.. 148

Приложения. Ошибка! Закладка не определена.

Библиографический список.. Ошибка! Закладка не определена.

Введение

Предмет теории вероятностей

Теория вероятностей изучает закономерности в массо­вых случайных явлениях. Поясним это на двух простых примерах.

1. Проводится испытание – бросается монета. Если ис­пы­тание проводится один раз, то предсказать его исход – выпаде­ние герба или цифры – невозможно, здесь царит слу­чай. Пусть теперь испытание проводится много раз, причем так, что при каждом следующем испытании воспроизводится комплекс ус­ловий, при которых проводилось предыдущее; в этом случае говорят, что проводится серия независимых ис­пытаний. Заме­чательным является то, что в этой ситуации случай исчезает: можно предсказать, что герб выпадет при­мерно в 50% случаев, причём этот прогноз тем точнее, чем больше проводится испы­таний. Этот прогноз подтвержда­ется многократными провер­ками, проводившимися в разное время учёными. Так, француз­ский учёный Ж.Л.Л.Бюффон бросал монету 4040 раз, герб выпадал в 2048 случаях; швед­ский учёный К.Пирсон бросал монету 24000 раз, герб выпа­дал в 12012 случаях; и так далее.

2. Пусть испытание состоит в бросании игральной кости, представляющей собой куб, грани которого занумеро­ваны цифрами 1–6. При однократном бросании предсказать исход невозможно, однако можно предсказать, что в длин­ной серии независимых бросаний каждая из цифр выпадает примерно в 1/6 части случаев, этот прогноз тем точнее, чем больше броса­ний.

Проиллюстрированное на двух примерах явление, со­стоящее в том, что процент наступления случайного события в длинной серии независимых испытаний не случаен, пред­став­ляет собой один из универсальных законов природы, по­лучив­ший название закона больших чисел. Теория вероятно­стей представляет собой математическую модель этого за­кона. Вво­димое в самом начале этой теории понятие "веро­ятность слу­чайного события" и связанные с ним правила по­зволяют дать строгую математическую формулировку за­кона больших чи­сел, дают подходы к вычислению в ряде важных для практики случаев процента наступления случай­ного события в длинной серии испытаний до того, как эти испытания проводятся, и тем самым – подходы к прогнози­рованию результата этих испыта­ний. Методы прогнозирова­ния по массовым случайным явле­ниям, развиваемые в тео­рии вероятностей, широко применя­ются в настоящее время в различных областях науки и практи­ческой деятельности че­ловека.

Данное учебное пособие написано на основе курсов лек­ций, прочитанных одним из авторов в Омском государст­вен­ном техническом университете, другим автором в Ом­ском филиале Московского государственного университета коммер­ции. Основная задача, которую ставили перед собой авторы, – не стремясь к максимальной строгости и охвату материала, предложить простую методику разъяснения ряда трудных для понимания узловых понятий и идей теории ве­роятностей. на­деемся, что эта задача отчасти выполнена.

В дополнениях I-III приведены об­разцы решения типовых задач, набор задач для использова­ния на практиче­ских занятиях и варианты контрольных за­даний для студентов заочной формы обучения.

Пособие предназначено для студентов инженерных и экономических специальностей широкого профиля, может быть использовано в качестве элементарного руководства ин­женерами и экономистами, применяющими в своей дея­тельно­сти методы теории вероятностей.

Краткий исторический очерк

Истоки теории вероятностей теряются в глубине веков. Еще в древнем Египте собирались статические данные о на­ро­донаселении. Этот факт говорит о том, что уже тогда была за­мечена возможность практических выводов по результатам массовых случайных явлений. Однако многие столетия дальше сбора статистических данных дело не шло. В этот период ника­ких специальных методов не возникает, идет на­копление материала.

В XVI веке появление работ Д. Кардано и Н. Тарталья[1] знаменует собой первый шаг в развитии вероятностных пред­ставлений. В работах этих ученых впервые формулиру­ются простейшие задачи из области азартных игр.

На роль случайностей в измерениях впервые обратил внимание великий Галилей[2]. И хотя он не дал аналитиче­ского анализа оценки ошибок наблюдений, многие выска­занные им положения оказали большое влияние на выра­ботку основных понятий теории ошибок и теории вероятно­стей.

Дальнейшее развитие теории вероятностей можно ус­ловно разбить на 4 периода[3].

первый период начинается с середины XVII века и про­должается до начала XVIII в. Он характеризуется воз­никнове­нием теории вероятностей как науки.

До середины XVII в. не было никакого общего метода решения вероятностных задач. Однако следующие 50 лет озна­меновались выдающимися достижениями в этой об­ласти. В разработку вопросов теории вероятностей были во­влечены крупнейшие ученые того времени. В первую очередь здесь следует назвать Паскаля[4], Ферма[5] и Гюйгенса[6]. В своих трудах они уже широко использовали теоремы сложения и умножения, ввели понятие математического ожидания, а также выяснили фундаментальное значение для теории вероятностей понятий зависимости и независимости случайных событий.

В 1657г. Гюйгенс пишет первую книгу по теории вероятностей "О расчете в азартных играх". Примечательно его высказывание: "… при внимательном изучении предмета читатель заметит, что имеет дело не только с игрой, но что здесь закладываются основы очень интересной и глубокой теории".

Итак, в рассматриваемый период теория вероятностей превращается в науку. Она начинает использоваться для реше­ния важных практических задач, находит свои первые приме­нения в демографии (наука о народонаселении), страховом деле и теории ошибок.

Начало второго периода связано с появлением в 1713г. книги Я.Бернулли[7] "Искусство предположений". В этой работе была строго доказана одна из важнейших теорем теории вероятностей, которая является простейшей формой

закона больших чисел. Эта теорема утверждает, что относительная частота события при достаточно большом числе испытаний сходится в определенном смысле к вероятности этого события. Теорема Бернулли позволила придать определенный смысл понятию вероятности и применить теорию вероятностей к самым разнообразным задачам статистики.

Выдающимся ученым Муавру[8] и Лапласу[9] принадлежит заслуга доказательства одной из простейших форм центральной предельной теоремы. Они впервые ввели в рассмотрение нормальный закон, который играет исключительную роль в самых разнообразных задачах теории вероятностей.

Великий немецкий математик К.Ф. Гаусс[10] доказал, что ошибки измерений подчиняются нормальному закону, и тем самым внес неоценимый вклад в теорию ошибок. Он также разработал метод обработки экспериментальных данных, который носит название "Метода наименьших квадратов". Здесь следует также отметить, что вывод нормального закона для случайных ошибок независимо от Гаусса и практически одновременно с ним получил малоизвестный американский математик Р. Эдрейн (1775–1843).

Второй период в развитии теории вероятностей завершается работами Пуассона[11], который доказал более общую, чем у Я. Бернулли, форму закона больших чисел. Ему также принадлежит заслуга применения методов теории вероятностей к задачам стрельбы. Имя Пуассона носит название один из важнейших законов распределения, который играет большую роль во многих задачах практики.

Следует отметить, что попытка Пуассона и некоторых других ученых применять теорию вероятностей к социальным явлениям вызвала оживленные споры и серьезные возражения в среде математиков и социологов. Появилось большое количество работ, посвященных неоправданным применениям теории вероятностей к жизни общества. Это привело к тому, что к теории вероятностей стали относиться скептически. А если еще учесть, что в это время недостаточно ясны были области приложения теории вероятностей в естественных науках, то становится понятным, почему интерес к ней на Западе резко упал.

Третий период в развитии теории вероятностей тесно связан с работами Петербургской математической школы. Следует отдать должное выдающемуся математику В.Я.Буняковскому (1804–1889), роль которого в распространении вероятностных идей в России переоценить нельзя. Он является автором первого курса теории вероятностей на русском языке и учителем великого русского математика П. Л. Чебышева[12], которого по праву можно назвать руководителем дореволюци­онной математической школы в России. Работы Чебышева в области теории вероятностей явились крупнейшим событием в математике. Они положили начало целому циклу глубоких исследований в области закона больших чисел. Его идеи оста­вили яркий след в развитии математики и предопределили надолго наперед направление и методы исследований массо­вых случайных явлений. "Вывел русскую теорию вероятностей на первое место в мире Пафнутий Львович Чебышев", – так оценил роль этого замечательного ученого академик А.Н. Кол­могоров[13].

Наиболее выдающимися учениками Чебышева, оста­вив­шими неизгладимый след в развитии теории вероятно­стей, яв­ляются А.А. Марков[14] и А.М. Ляпунов[15]. Маркову принадлежит обобщение закона больших чисел на случай зависимых случайных величин. Его работы положили начало бурно развивающейся в настоящее время теории случайных функций. Ляпунову мы обязаны первым доказательством центральной предельной теоремы при весьма общих усло­виях.

Современный, четвертый период характеризуется ис­ключительным подъемом интереса к теории вероятностей в самых различных областях человеческой деятельности. Этот интерес стимулировал бурное развитие многих направлений теории вероятностей.

Российская школа теории вероятностей, которая в на­стоящее время по праву занимает в мировой науке ведущее ме­сто, решила ряд принципиальных вопросов. В частности, ака­демикам С. Н. Бернштейну и А. Н. Колмогорову принадлежат основополагающие работы в аксиоматическом построении теории вероятностей.

Большой вклад в развитие теории вероятностей внесли российские ученые А.Я. Хинчин, Б.В. Гнеденко, Е. Б. Дынкин, В.С. Пугачев, А.Н. Ширяев, А.А. Боровков, Ю.А. Розанов, Ю.В. Прохоров, И.И.Гихман, А.В. Скороход и другие. теория вероятностей продолжает интенсивно развиваться в настоящее время.

Глава 1. Основные понятия и правила теории вероятностей

Элементы комбинаторики

Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего, в частности, вопрос о количестве комбинаций из n элементов по т, которые можно составлять тем или иным способом. Мы рассмотрим три таких способа.

1. Сочетания

Комбинации из n элементов по т, отличающиеся только составом, называются сочетаниями. Число сочетаний из n элементов по т равно

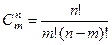, (2)

где n! = .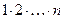

Пример 1. В группе 30 человек. необходимо выбрать трех делегатов на конференцию. Сколько существует способов это сделать?

Решение. Каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки отличаются только по составу, то есть являются сочетаниями из 30 элементов по 3.Их количество находим по формуле (2):

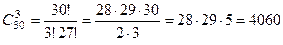способов.

Пример 2. В шахматном турнире участвует 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение. Каждая партия играется двумя участниками из 16. Пары игроков отличаются от других пар только составом, то есть представляют собой сочетания из 16 элементов по 2. По формуле (2) найдем:

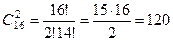партий.

2. Размещения

Комбинации из n элементов по т, отличающиеся соста­вом или порядком элементов, называются размещениями. Число размещений из n элементов по т равно

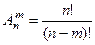. (3)

Пример 1. В группе 30 человек необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки отличаются как по составу, так и по порядку, то есть являются размещениями из 30 элементов по 3. Их количество находим по формуле (3):

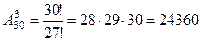способов.

Пример 2. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе 11 дисциплин.

решение.Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания, то есть число размещений из 11 по 5 находим по формуле (3):

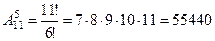вариантов.

3. перестановки

Комбинации из n элементов по n, отличающиеся поряд­ком, называются перестановками. Число перестановок из n элементов равно

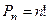(4)

Пример 3. Порядок выступления семи участников кон­курса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

решение. каждый вариант жеребьевки отличается только порядком участников конкурса, то есть является пере­становкой из 7 элементов. Их число находим по формуле (4):

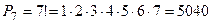вариантов.

Приведем пример на вычисление вероят­ности случайного события с использова­нием формул комбина-торики.

Пример 4. Из 30 студентов 10 имеют спортивные раз­ряды. Какова вероятность того, что выбранные наудачу 3 сту­дента – разрядники?

решение. Пусть событие А состоит в том, что все 3 выбранных наудачу студента – разрядники. Общее число вариантов выбора трех студентов из 30 равно 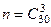, так как комбинации из 30 студентов по 3 отличаются только составом студентов. Точно так же число случаев, благоприятствующих событию А, равно 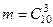. По формуле (1) имеем

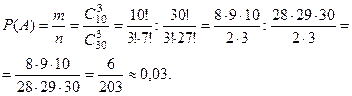
Действия над событиями

Пусть с испытанием связаны события А, В.

Определение 1. Суммой событий А, В называется третье событие С, состоящее в наступлении хотя бы одного из событий А, В:

С = А + В.

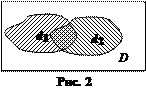Пример 1. Испытание: берут наугад точку в области D (рис 2). Рассмотрим события:

А – попадание в область d₁;

В – попадание в область d₂;

С– попадание в заштрихованную область.

Тогда С = А + В.

Определение 2. Произведением двух событий А, В назы­вается третье событие С, состоящее в одновременном наступ­лении этих событий: С = А · В.

Пример 2. Испытание: берут наугад точку в области D (рис 2). Рассмотрим события:

А – попадание в область d₁;

В – попадание в область d₂;

С – попадание в общую часть областей d₁ и d₂.

Тогда С = А · В.

Определение 3. Событие В называется противополож­ным событию А, если оно состоит не в наступлении события А:

В = .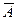

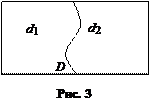Пример 3. Испытание: берут наугад точку в области D (рис 3).

Событие А: попадание в область d₁;

Событие В: попадание в область d₂.

Тогда В = .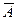

Замечание. Укажем другие обозначения для введенных операций:

А + В Û А или В;

А · В Û А и В;

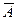Û не А.

Сумма событий – операция "или";

произведение событий – операция "и";

переход к противоположному событию – операция "не".

Из определения суммы и произведения событий вытекают следующие свойства введенных трех операций.

1) А + А = А; 8) А · W = А;

2) А + Æ = А; 9) А · В = В · А;

3) А + W = W; 10) (А · В) · С = А · (В · С);

4) А + В = В + А; 11) (А + В) · С = А · С + В · С;

5) (А + В) + С = А + (В + С); 12) ;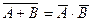

6) А · А = А; 13) .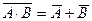

7) А · Æ = Æ;

Докажем свойства 12 и 13, остальные 1–11 очевидны.

Событие А + В состоит в наступлении хотя бы одного из событий: А, В, следовательно событие 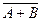состоит в ненаступлении ни одного из событий А, В. Тот же смысл имеет произведение 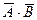, то есть 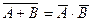, что и требовалось.

Событие 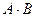состоит в одновременном наступлении событий А, В, следовательно событие 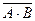состоит в ненаступлении хотя бы одного из событий А или В. Тот же смысл имеет сумма 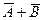, то есть 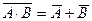, что и требовалось.

Множество элементов, удовлетворяющих указанным свойствам, называется алгеброй Буля. Алгебра Буля играет важную роль в математической логике, являющейся одной из теоретических основ ЭВМ.

В математической логике применяются следующие названия указанных операций: "или" – дизъюнкция; "и" – конъюнкция; "не" – отрицание.

Решение.

I способ. По определению вероятности (1) (гл.1§1) и по формуле (2) имеем:

а) Р(бб) ;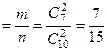

б) Р(чч) .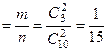

II способ. По формулам (6) и (7) имеем:

а) Р(бб) = Р (1^й белый и 2^й белый) = Р(1^й белый) ·Р (2^й б/ 1^й б) =

.

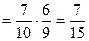б) Р(чч) = Р (1^й черный и 2^й черный) = Р(1^й ч) ·Р (2^й ч/ 1^й ч) =

.

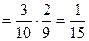в) Р(одного цвета) =Р (1^й б и 2^й б или 1^й ч и 2^й ч) = Р(бб + чч) =

= Р(бб) + Р (чч) = = .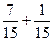

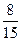г) I способ.

Р (разного цвета) = Р (б·ч + ч·б) = Р (б·ч) + Р(ч·б) =

.

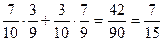II способ.

Р (разного цвета) = 1 – Р (одного цвета) = 1 – = .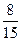

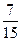Рис. 7

Испытание: из наугад выбранной урны наугад берут один шар. Найти вероятность того, что шар белый.

обозначим: событие А – выбран белый шар, Р(А) – ?.

Введем три предположения (гипотезы):

Н₁ – выбран шар из I-ой урны;

Н₂ – выбран шар из II-ой урны;

Н₃ – выбран шар из III-ей урны.

Очевидно, эти гипотезы являются несовместными событиями, одно из которых обязательно реализуется в результате испытания, то есть

.

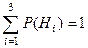Найдем вероятности следующих событий:

, , .

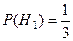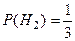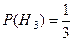Р(А·Н₁) = Р(Н₁)Р(А/Н₁), ;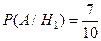

Р(А·Н₂) = Р(Н₂)Р(А/Н₂), ;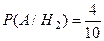

Р(А·Н₃) = Р(Н₃)Р(А/Н₃), .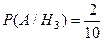

Откуда имеем:

Р(А) = Р (АН₁ + АН₂ + АН₃) = Р (АН₁) + Р (АН₂) + + Р (АН₃) .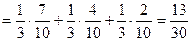

Перенесем эту задачу в следующую общую ситуацию: событие А может наступить при одной из n взаимоисключающих гипотез Н₁, Н₂, …, Н_n. Рассуждая аналогично, применяя формулы сложения, умножения событий, получаем формулу

Р(А) = Р(Н₁)Р(А/Н₁)+Р(Н₂)Р(А/Н₂) + … +Р(Н_n)Р(А/Н_n), (9)

которая называется формулой полной вероятности.

Вычисление вероятностей гипотез при наличии дополнительной информации. Формула Байеса.

Рассмотрим две задачи.

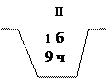рис. 8

1. Известно, что в соседней комнате проводилось следующее испытание: из наугад выбранной урны (рис. 8) брали наугад один шар. Какова вероятность того, что его брали: а) из первой урны (Н₁); б) из второй урны (Н₂)?

В этой ситуации оба предположения следует считать равновозможными:

.

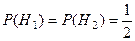2. Известно, что в соседней комнате проводилось то же испытание, и был вынут белый шар. какова вероятность, что шар взят: а) из первой урны; б) из второй урны.

В этой ситуации гипотезы нельзя считать равновоз­мож­ными: в первой урне значительно больше белых шаров, чем во второй. Как в этой ситуации найти вероятности гипо­тез?

Эта задача может быть в общем виде сформулирована так:

1) в данном испытании интересующее нас событие А может наступить при одной из n взаимоисключающих гипотез Н₁, Н₂, …, Н_n;

2) известно, что испытание проведено и его результат известен: наступило событие А. Как найти вероятности Р(Н₁/А), Р(Н₂/А), …, Р(Н_n/А)?

Утверждение. В указанной ситуации справедлива формула:

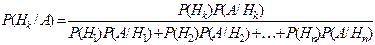, (10)

которая называется формулой Байеса.

Доказательство. По формуле (7) имеем

Р(А·Н_k) = Р(А) · Р(Н_k/А),

Р(А·Н_k) = Р(Н_k) · Р(А/Н_k).

Откуда, учитывая формулу (9), получаем

.

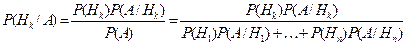Решение.

Р (40≤ x≤ 60) = Р(x = 40) + Р(x = 41) + Р(x = 42) + … +

+ Р(x = 60) = .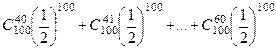

Мы видим: если в схеме Бернулли число испытаний n велико, то подсчет вероятностей вида P(m₁ ≤ x≤ m₂) с помощью формулы Бернулли весьма затруд­нен.

укажем приближенную формулу для подсчета таких ве­роятностей, доказанную независимо французскими математи­ками Муавром и Лапласом.

для этого вначале введем функцию, которая называется функцией Лапласа и обозначается Ф(х):

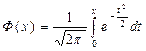. (12)

Укажем график и некоторые свойства этой функции.

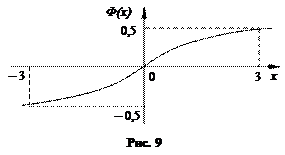1⁰. Ф(0) = 0;

2⁰. Ф (– х) = – Ф(х);

3⁰. если | x | ≥ 3, то Ф (х) » ± 0,5 с большой точностью.

Для функции Лапласа имеются таблицы.

Теорема 2. В схеме Бернулли при достаточно большом числе испытаний справедлива приближенная формула:

P(m₁ ≤ x ≤ m₂) » 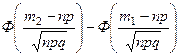. (13)

эта формула называется интегральной формулой Муавра-Лапласа. Доказательство этой формулы приводится в §3 главы 3. Вычисления показывают, что эта формула является практически точной при n ≥ 30.

Вернемся к решению примера 2.

решение. Здесь n =100, p = q = 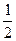. По формуле Муавра-Лапласа найдем

Р (40 ≤ x ≤ 60)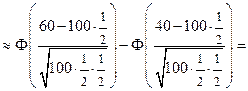

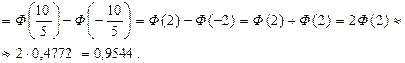
Замечание. Интегральная формула Муавра-лапласа указывает правила вычисления вероятности неравенств вида P(m₁ ≤ x ≤ m₂) в схеме Бернулли при большом числе испытаний. Укажем правило вычисления вероятностей P(x=k) в этой ситуации.

Рассмотрим функцию

.

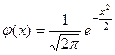Очевидно, φ(х) связана с функцией Лапласа равенством

.

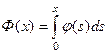При большом числе испытаний справедлива приближенная формула

. ( )

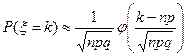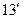эта формула называется локальной формулой Муавра-Лапласа. Для функции (13^') имеются таблицы.

Глава 2. Случайные величины

Пример 2.

.

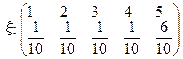
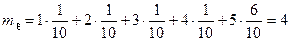Помнить: математическое ожидание характеризует центральное значение случайной величины с учетом возможных значений и их вероятностей: маловероятные значения вносят малый вклад в формирование математического ожидания, наиболее вероятные значения вносят основной вклад.

Свойства математического ожидания.

1⁰. М [ a ] = а.

Математическое ожидание неслучайной величины равно самой величине.

2⁰. М [ а x ] = a M [ x ].

Неслучайный множитель выносится за знак математиче­ского ожидания.

3⁰. M [ x + h ] = M [ x ] + M [ h ].

Математическое ожидание суммы случайных величин равно сумме математических ожиданий.

4⁰. Если x, h статистически независимы, то

M [ x · h ] = M [ x ] · M [ h ].

Доказательство.

1. Имеем: 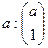, откуда получаем m_a = 1· a = a.

2. Пусть

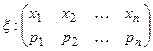, тогда ,

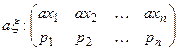откуда М [ а x ] = ax₁· p₁ + ax₂· p₂ +…+ ax_n· p_n = a M [ x ].

Для наглядности далее будем предполагать, что x, h при­ни­мают два возможных значения:

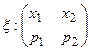; h .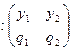

3. x + h : ;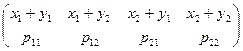

M [ x + h ] ;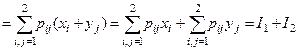

I₁ = p₁₁ x₁ + p₁₂ x₁ + p₂₁ x₂ + p₂₂ x₂ = (p₁₁ + p₁₂)x₁ + (p₂₁ + p₂₂)x₂.

;

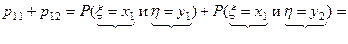
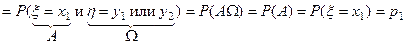доказано: р₁₁ + р₁₂ = р₁­, аналогично получим: р₂₁ + р₂₂ = р₂,

тем самым I₁ = p₁x₁ + p₂x₂ = M [ x ].

Также доказывается, что I₂ = M [ h ].

4. В силу теоремы умножения для независимых событий имеем: x · h : .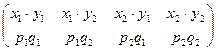

Тогда

M [ x · h ] = p₁q₁x_1­y₁ + p₁q₂x_1­y₂ + p₂q₁x_2­y₁ + p₂q₂x_2­y₂ =

= (p₁x₁ + p₂x₂) · (q₁y₁ + q₂y₂) = M [ x ] · M [ h ].

Пример.

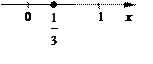Испытание: берут наугад точку x на чи­словой оси так, что значения на от­резке [0, 1] равновозможны, остальные значе­ния невозможны. Очевидно, x – непре­рывная случайная величина.

Найдем

.

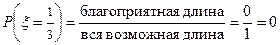Закон распределения непрерывной случайной вели­чины может быть задан двумя способами:

1. с помощью функции распределения F (x);

2. с помощью плотности вероятности f (x).

Функция распределения

Пусть с испытанием связана непрерывная случайная величина x.

Зафиксируем произвольное число х. В зависимости от случая возможны три исхода испытания:

x > x, x = x, x < x.

Каждое из этих трех событий случайно, поэтому имеет смысл говорить об их вероятности. Обозначим

F (x) = p (x < x).

Функция F(x) называется функцией распределения случайной величины x.

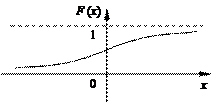Рис. 11

свойства функции распределения

1⁰. 0 ≤ F (x) ≤ 1;

2⁰. F (x) монотонно не убывает (рис. 11);

3⁰. F (– ¥) = 0, F (+ ¥) = 1;

4⁰. P (a<x< b) = F (b) – F (a).

доказательство.

1. Это свойство вытекает из того, что вероятность любого события есть число, принадлежащее [0, 1].

2. Это свойство вытекает из того, что при увеличении х интервал ( – ¥, х) расширяется, поэтому вероятность попадания в этот интервал не уменьшается.

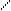3. F (– ¥) ,

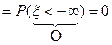F (+ ¥) .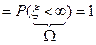

4. Имеем:

F (b) = P (x < b) = =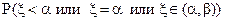

= P (x < a) + P (x = a) + P (x Î (a, b)) = F (a) + 0 + P (a<x< b).

Отсюда вытекает требуемое равенство 4⁰.

Замечание. Функция распределения F (x) имеет смысл и для дискретных случайных величин. Например, функция распределения случайной величины

x :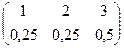

представляет собой кусочно-постоянную функцию, график которой изображен на рис. 12 (кружок означает, что в этом месте отсутствует точка на графике).

Рис. 12

Проверим это для случаев х >3, 2≤ х< 3. В первом случае имеем

F (x) = P (x < x) = P (x = 1 или x = 2 или x = 3) =

= P (x = 1) + P (x = 2) + P (x = 3) = 0,25 + 0,25 + 0,5 = 1.

Во втором случае

F (x) = P (x = 1 или x = 2) = Р (x = 1) + Р (x = 2) =

= 0,25 + 0,25 = 0,5.

Оставшиеся случаи 1≤ х< 2, x<1 предлагаем рассмотреть са­мостоятельно.

Плотность вероятности

[ ] Пусть с испытанием связана непрерыв­ная случайная величина x.

Плотностью вероятности случайной величины x в точке х называется предел отношения вероятности попадания в отрезок [x, x + Dx] к длине отрезка Dx при условии, что отрезок стягивается к точке х:

.

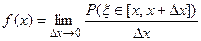Нестрого говоря, плотность вероятности – это вероятность попадания в отрезок длины 1.

Свойства плотности вероятности:

1⁰. f (x) ≥ 0 при всех х.

2⁰. P (x Î (a,b)) =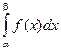

вероятность попадания в интервал равна заштрихованной площади (рис. 13).

Рис. 13

3⁰. Площадь S бесконечной фигуры, ограниченной графи­ком плотности f (x) и осью абсцисс, равна 1 (рис. 13): S = 1.

Доказательство.

1. Это свойство вытекает из того, что предел неотриц