Анализ полученной модели и выбор метода ее решения

Основой для вычисления значений выходных характеристик описательной модели служит составленный на ее базе алгоритме решения задачи ЭВМ. Разработка и программирование такого алгоритма при соответствующих навыках принципиальных сложностей не представляет. Более сложной является организация вычислительного процесса для нахождения выходных характеристик, лежащих в допустимых областях, особенно для большого числа факторов модели. В ряде случаев в решении этой задачи могут оказать помощь методы оптимального планирования экспериментов.

Значительно большие вычислительные трудности вызывает поиск решений по оптимизационным моделям. Самая совершенная и адекватная описываемому процессу математическая модель без нахождения метода поиска оптимальных значений бесполезна и не может быть практически использована. Эти методы зачастую рассматриваются в рамках направления, которое в настоящее время получило название теории принятия оптимальных решений.

Основную роль при разработке алгоритма поиска оптимальных решений играют характер факторов математической модели, число критериев оптимальности, вид целевой функции и уравнений связи.

В зависимости от характера факторов, на базе которых построена оптимизационная модель, различают принятие решений при определенности, риске, неопределенности, при сочетании риска и неопределенности.

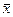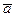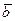Выбор решений при определенности осуществляется для детерминированных моделей, т.е. моделей, включающих только управляемые переменные и константы и в выражения (2.12) и (2.13). При этом каждому набору переменных соответствует единственное значение целевой функции.

Выбор решений при риске происходит в случае стохастических моделей, т.е. моделей, включающих переменные 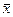, константы 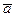и 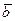и случайные факторы 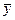с известными законами распределения. В этом случае определенному набору переменных соответствует множество частных (случайных) результатов, причем вероятности этих результатов лицо, принимающее решение, может определить путем многократного проигрывания модели на ЭВМ.

Выбор решения при неопределенности имеет место для моделей, включающих переменные 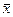, константы 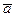и 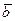и неопределенные факторы 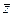. При этом набору переменных соответствует множество возможных частных результатов, зависящих от значений неопределенных факторов .

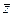Понятие решений по многим критериям оптимальности характеризуется наличием специальных критериев, на основе которых, как правило, формируется единая целевая функция оптимизационной модели.

Вид целевой функции и ограничений определяет выбор одного из трех основных методов решения экономико-математических моделей: аналитического исследования; исследования при помощи численных методов; исследования алгоритмических моделей с помощью методов экспериментальной оптимизации на ЭВМ.

Аналитические методы отличаются тем, что помимо точного значения искомых переменных они могут давать оптимальные решения в виде готовой формулы, куда входят характеристики внешней среды и начальные условия, которые исследователь может изменять в широких пределах, не меняя самой формулы. Это очень удобно, поскольку, варьируя эти факторы, можно охватить широкий круг условий функционирования объектов рассматриваемого класса. Однако на практике таких моделей сравнительно немного, и применяются они для ограниченного числа довольно простых задач. К аналитическим методам относятся, например, методы нахождения безусловного экстремума и множителей Лагранжа для задач на условный экстремум и ряда других.

При численных методах оптимальное решение получается путем многократных расчетах по определенному алгоритму, реализующему тот или иной численный метод. В качестве исходных данных для вычислений используются числовые значения параметров объекта, внешней среды и начальных условий. Численные методы являются итеративными процедурами: для проведения следующего шага расчетов (при новом значении управляемых переменных) используются результаты предыдущих расчетов, что позволяет получать в процессе вычислений улучшенные результаты и тем самым находить оптимальные решения. Численные методы, хотя и дают оптимальные решения лишь для конкретных значений факторов модели, применяются значительно шире. Они являются основным методом решения для моделей математического программирования, к которым сводится значительная часть производственных оптимизационных задач.

Характерной особенностью численных методов является то, что для типовых формулировок моделей математического программирования они разработаны не только для уровней принципов оптимизации и алгоритмов, но и до уровня программ, входящих в состав математического обеспечения большинства современных ЭВМ. Вновь разрабатываемые программы отдельных численных методов помещаются в Общегосударственный фонд алгоритмов и программ. Это освобождает разработчика моделей от необходимости разрабатывать алгоритмы и программы поиска оптимального решения для моделируемого объекта, существенно сокращает процесс получения результатов.

Первые два метода нахождения оптимальных решений ЭВМ могут быть применены только для моделей математического программирования, т.е. однокритериальных моделей, в которых единственная целевая функция и ограничения заданы аналитически.

Все алгоритмические, в том числе и имитационные, модели представляют собой модели типа «черного ящика». Алгоритмические модели не способны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются пользователем. Это означает, что они обеспечивают расчет значений выходных характеристик при наличии на входе модели всей необходимой информации. Поэтому для получения полной информации о поведении моделируемого объекта необходимо осуществлять многократный прогон модели при всевозможных значениях параметров объекта и характеристик внешней среды.

Свойства конкретной алгоритмической модели, на которых базируется алгоритм поиска оптимальных решений, например ее линейность или выпуклость, могут быть определены только в процессе экспериментирования с ней, в связи с чем для решения моделей этого класса используются так называемые методы экспериментальной оптимизации на ЭВМ.

При экспериментальной оптимизации на ЭВМ производится пошаговое приближение к оптимальному решению на основе результатов расчета по алгоритму, моделирующему работу исследуемой системы. Методы экспериментальной оптимизации на ЭВМ базируются на принципах поиска оптимальных решений в численных методах, но в отличие от них все работы по разработке алгоритмов и программы оптимизации выполняет разработчик модели. Имитационное моделирование задач, содержащих случайные параметры, принято называть статическим моделированием.

Поиск оптимальных решений по имитационным моделям, особенно по имитационным статистическим моделям, чрезвычайно трудоемок. В настоящее время наметилось два пути решения этой проблемы: использование теории планирования экспериментов и разработка тех или иных эвристических правил поиска, основанных на формализации действий человека, принимающего решение. Имитационные ЭВМ, оптимизация решения которых основана на эвристических правилах выбора наилучшего варианта, принято называть эвристическими моделями, а их использование – эвристическим моделированием.

Заключительным шагом создания модели является составление ее описания, которое содержит сведения, необходимые для изучения модели, ее дальнейшего использования, а также все ограничения и допущения. Тщательный и полный учет всех факторов при построении модели и формулировке допущений позволяет оценить точность модели, избежать ошибок при интерпретации ее результатов.

1. Перечислите основные цели, для которых строится математическая модель сложного объекта. Раскройте их содержание.

2. Перечислите основные задачи, решение которых необходимо для построения математической модели объекта и управления им.

3. Какие источники получения информации для построения математической модели сложного объекта Вы знаете?

4. Какие вопросы необходимо решать на стадии подготовки исходной информации в процессе обследования объекта управления и его окружения?

5. Перечислите в необходимом порядке основные этапы построения сценария процесса функционирования моделируемого объекта управления

6. Раскройте суть основных процедур построения канонической модели объекта управления. составляющих содержание 1-го этапа формирования сценария функционирования моделируемого объекта.

7. Как проводится классификация факторов при формировании концептуальной модели по признаку возможности количественного описания?

8. Как проводится классификация факторов при формировании концептуальной модели по степени определенности?

9. Как проводится классификация факторов при формировании концептуальной модели по их роли в модели?

10. Каков состав и содержание основных процедур построения иерархической структуры объекта управления? Как представляется иерархическая структура модели объекта

11. Каков состав и содержание основных процедур построения канонических моделей для отдельных элементов объекта управления? Опишите основные правила согласования всего множества их входов и выходов

12. Как осуществляется изучение места и роли каждого элемента модели внутренней структуры объекта в процессе его функционирования?

13. Как должна осуществляться увязка элементарных процессов в единую модель функционирования объекта на одноименном этапе формирования сценария функционирования объекта управления?

14. Чем иллюстрируется описание функционирования объекта управления? Что составляет суть технологической карты и технологической диаграммы? Что такое многофункциональная диаграмма операций? Приведите примеры.

15. Дайте определение и представьте назначение концептуальной модели. Что такое цель и критерий управления? Представьте основные виды целей управления и основные формы критерия управления. Роль фактора времени в критерии управления.

16. Представьте и объясните структуру системы управления с обратной связью. Что такое обратная связь и ее роль в процессе управления?

17. Представьте и объясните структуру иерархической системы управления

18. В чем суть процедур формирования дерева целей. Проиллюстрируйте их на графическом примере.

19. Как осуществляются процедуры формирования критериев и и ограничений. Представьте очередность их проведения.

20. Представьте основную суть методов и процедур отбора существенных факторов при формировании математической модели

21. Опишите основную суть использования методов математической статистики при моделировании сложных экономических систем и объектов

22. Что Вам известно об использовании и сути использования методов экспертных оценок при математическом моделировании экономических процессов и систем?

23. В чем суть основных операций установления качественных зависимостей при формировании математической модели?

24. Опишите основные процедуры этапа моделирования: построение и анализа математической модели

25. В чем суть выполнения этапа моделирования: численное представление математической модели? Что такое аппроксимация? Приведите виды основных аппроксимационных функций. Что такое интерполяция?

26. Опишите этап моделирования: анализ полученной модели и выбор метода ее решения. Приведите классификацию основных методов решения математических моделей.

27. В чем суть аналитических методов решения математических моделей?

Глава 3.
МЕТОДЫ ПОИСКА РЕШЕНИЙ НА МОДЕЛЯХ

3.1. Методы поиска оптимальных решений для
однокритериальных моделей с детерминированными факторами

Аналитические исследования

При аналитическом исследовании моделей математического программирования используются общеизвестные методы отыскания экстремальных значений – классические методы оптимизации. В качестве основного математического аппарата применяется дифференциальное исчисление для нахождения значения переменных, максимизирующих или минимизирующих целевую функцию. Для использования этих методов математическую модель необходимо преобразовать в систему уравнений относительно искомых величин. Результатом решения аналитической модели является либо получение формул для вычисления искомых величин, либо приведение уравнений к виду, для которого решения известны. При моделировании сложных процессов осуществление таких преобразований является достаточно сложной задачей.

В классических задачах оптимизации целевая функция 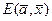и уравнение связи 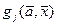должны быть по крайней мере дважды дифференцируемыми функциями, а ограничения – иметь вид строгих равенств.

Классические задачи оптимизации разделяются на два подкласса:

1. Задач а отыскания безусловного экстремума. В этих задачах отсутствуют ограничения на область допустимых значений переменных управления 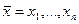, т.е. отсутствует функция 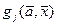. Постановка задачи имеет вид

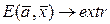. (3.1)

2. Задачи отыскания условного экстремума с ограничениями типа равенств. Постановка задачи имеет вид

;

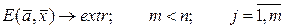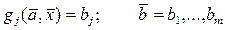. (3.3)

где 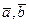– векторы констант модели.

Задача типа (3.2) в результате применения метода множителей Лагранжа сводится к задаче (3.1). При этом исходная функция 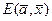заменяется функцией Лагранжа

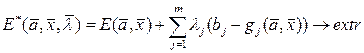, (3.3)

где 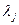- неопределенные коэффициенты.

Классический подход к решению задачи безусловной оптимизации состоит в использовании необходимого условия экстремума функции. Необходимым (но не достаточным) условием существования экстремума непрерывной функции является равенство нулю всех ее частных первых производных, т.е. условия 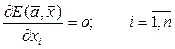, либо для (3.3)

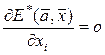; (3.4)

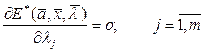. (3.5)

Корни систем уравнений (3.4), (3.5) называются стационарными. Эти точки «подозрительны» на предмет нахождения в них максимума, минимума или седловых точек функций 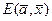, либо .

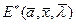Процедура решения задачи оптимизации классическим методом состоит из следующих этапов:

получение и решение системы уравнений (3.4) или (3.5) с целью определения всех стационарных точек;

анализ тем или иным способом стационарных точек для выявления всех максимумов (минимумов) Функции;

сравнение между собой максимальных (минимальных) значений функций 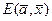, 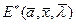с целью определения глобального максимума (минимума).

Получаемые в процессе решения системы уравнений (3.5) значения коэффициентов 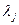характеризует влияние ограничений на нахождение оптимальных значений. При 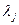, близком к нулю, j-е ограничение несущественно влияет на нахождение оптимума. Информация о значениях коэффициентов 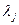, полученная в результате расчета, дает возможность проверить правильность формирования концептуальной модели, например, сопоставить приоритетность ограничений концептуальной модели с приоритетностью, получаемой в результате расчета. Это может привести к пересмотру концептуальной модели, исключению одних и включению других (новых) ограничений.

Зачастую аналитическое решение систем уравнений удается получить в виде параметрических формул

,

что позволяет определить влияние изменения различного рода факторов модели на оптимальность решения, в том числе оценивать чувствительность полученного решения к действию случайных и неопределенных факторов.

Несмотря на принципиальную ясность в отношении классических методов решения задач безусловной оптимизации, на этом пути могут встретиться вычислительные трудности, которые делают необходимым поиск соответствующих методов решения. Так, только для систем линейных уравнений любого порядка разработаны точные методы нахождения решения, например методы Крамера, Гаусса и др. В общем же в случае уравнения типа (3.4), (3.5) являются нелинейными. Для отыскания точного решения произвольной системы уравнений высокого порядка не существует какой-либо надежной вычислительной схемы. Для определения приближенного решения может быть использован метод Ньютона и его модификации.

Введение ограничений типа неравенства и ограничений на положительность переменных, что принципиально важно для экономических исследований, приводит к необходимости поиска решений подобных аналитических моделей методом Куна-Таккера, являющимся одной из разновидностей численных методов.