Построение и анализ математической модели

Результаты выполнения этапа «Формирование концептуальной модели» оформляются в виде постановки прикладной задачи моделирования (иногда ее называют техническим заданием на проектирование модели исследуемого объекта). Хотя структура такого документа не регламентирована, целесообразно включить в него следующие пункты.

1. Наименование задачи, отражающее ее сущность, и ее краткое обозначение.

2. Цель разработки модели, т.е. содержание вопросов, которые стремятся решить с помощью данной модели.

3. Организационно-экономическая сущность задачи, в том числе принципиальная новизна, возможность внедрения в существующие системы, пути получения экономического эффекта.

4. Постановка задачи, где формулируется содержание задачи в формально-операторной или словесной форме с указанием критериев оптимальности и ограничений, т.е. описывается концептуальная модель объекта. Концептуальная модель может сопровождаться комплексом служебных моделей: иерархической, внутренней структуры, моделей отдельных операций, информационно-процедурных и т.д., поясняющих ее содержание.

5. Описание входной информации модели (числовые значения известных характеристик, параметров процесса, начальных условий) и вид ее задания (таблицы, графики, отдельные числовые значения, диапазоны изменения, законы распределения вероятностей и т.п.).

6. Описание возможных альтернатив решения поставленной задачи, состав переменных, их диапазоны изменения.

7. Периодичность и расписание решения – указываются либо интервалы времени между двумя решениями, либо моменты, в которые требуется решить задачу, либо условия, при которых становится необходимым ее решение. Задаются приемлемое время, затрачиваемое ЭВМ на решение задачи, и режим ее работы (в реальном масштабе времени или в пределах допустимого времени).

8. Вид представления результатов моделирования (управляющие сигналы в масштабе реального времени либо результаты счета, представляемые массивами чисел, графиками, таблицами, табуляграммами и т.д.).

9. Точность определения искомых характеристик.

10. Тип ЭВМ и языки программирования, на которых желательно решение задачи.

11. Календарный план проведения разработки модели и получения результатов и другие вопросы организационного и финансового содержания.

При формулировке прикладной задачи моделирования особое внимание следует обратить на фактор времени. Фактор «время» применительно к модели может принимать различные смысловые значения. Прежде всего для определения временной области использования разрабатываемой модели необходимо установить предполагаемую дату ввода модели в эксплуатацию Т_Н.

Календарную дату снятия модели с эксплуатации Т_М в процессе разработки модели установить нельзя, но можно и нужно определить условия, при которых модель нуждается в снятии с эксплуатации и доработке, а может быть, и замене новой моделью. К таким условиям относятся изменения в структуре окружения или в структуру моделируемого объекта, приводящие к изменения структуры модели: введению новых факторов, появлению новых или отмене действующих критериев или ограничений, замене функциональных соотношений между переменными, изменению состава элементов объекта, связей между ними и т.п. Они вытекают из сценария функционирования объекта и обязательно оговариваются в п. 3 технического задания.

Изменение значений отдельных факторов в процессе функционирования объекта приводит к необходимости неоднократного использования модели в течение периода ее жизни и появлению временного параметра Т_Р – периода времени между расчетами по модели, определяющего регламент ее использования. В зависимости от целей, которые ставит перед собой заказчик, параметр Т_Р может быть величиной постоянной или переменной. Специфика работы объекта может потребовать строгого периодического нахождения по модели его оптимальных параметров (например. составление ежемесячного плана предупредительного ремонта оборудования по результата его предшествующей эксплуатации).

Для оптимизационных моделей необходимость повторных расчетов определяется изменением входных характеристик моделей, приводящих к выходу расчетных показателей модели за пределы допуска (другими словами, определенное ранее оптимальное решение становится неоптимальным и требуется провести перерасчет). Условия проведения повторных расчетов, определяющие регламент использования модели, формируется в п.7 технического задания.

Моделируемая операция охватывает определенный временной период функционирования объекта Т_М, например, модель формирования годовой производственной программы предприятия. Однако в ряде случаев в модели бывает необходим учет ретроспективных или перспективных данных, что приводит к увеличению периода протекания операции Т_М. Так, при условии значительных опережений (например, 6 месяцев) вы изготовлении деталей по отношению к сборке для модели формирования годовой производственной программы следует рассматривать уже полуторагодовой период.

В динамических моделях всегда присутствует фактор текущего «модельного» времени t_М, изменение которого сопровождается изменением состояния объекта, т.е. изменением как промежуточных факторов, так и с итоге выходных характеристик объекта. Таким образом, в описании модели обязательно должны быть отражены характеристики Т_Н (Т_К), Т_Р, Т_М, t_М.

С формальной точки зрения назначение каждого объекта (или его отдельного элемента) состоит в том, чтобы преобразовать входные сигналы в выходные. Описательная математическая модель для любого объекта могла бы представлять систему соотношений вида

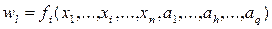, (2.11)

где w_l – выходные характеристики объекта; 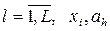– факторы, на базе которых строится модель объекта (параметры, характеристики окружения, начальные условия, время); .

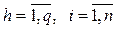Однако на практике получение адекватной исследуемому явлению модели такого вида, когда характеристики процесса являются явными функциями от входных факторов, бывает достаточно редко. В общем случае для сложных производственно-экономических систем эта задача может оказаться непосильной, что существенно сужает область использования «классических» методов исследования экономических операций (линейное, нелинейное и динамическое программирование, теория массового обслуживания, задача управления запасами, ремонта и замены оборудования и др.). Поэтому для описания и исследования таких объектов в последнее время стало интенсивно развиваться новое направление – имитационное моделирование.

Математическая формализация

Чтобы моделировать функционирование объекта, необходимо знать или предположить известными два из трех элементов. В связи с этим при моделировании отдельных компонентов или элементов объекта сталкиваются с задачами трех типов. Если известны уравнения, описывающие поведение объекта, то путем решения прямой задачи можно найти реакцию объекта на заданный входной сигнал. Обратная задача – по заданному математическому описанию и известной реакции найти входной сигнал, вызывающий этот отклик, – в практике моделирования производственно-экономических систем встречается редко. Если математическое описание объекта неизвестно, но имеются или могут быть заданы совокупности входных и соответствующих им выходных сигналов, имеем дело с задачей идентификации объекта.

Основным методом решения задач идентификации при моделировании производственно-экономических объектов является метод «черного ящика», или, как его еще называют, кибернетическое моделирование.

Сущность метода состоит в том, что при исследовании объектов они рассматриваются как недоступный для наблюдения, изучения и описания «черный ящик», имеющий определенные входы и выходы. Вследствие сложности устройства «черного ящика», т.е. изучаемого объекта, возможно лишь наблюдать состояние входов в него и соответствующих им выходов, т.е. изучать поведение, не зная его внутреннего устройства. Так, например, в экономических исследованиях дл нахождения производственной функции входами считают затраты ресурсов , а выходами – произведенную продукцию. Сопоставляя входы и выходы за ряд моментов времени, находят такие параметры 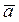производственной функции 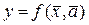, при которых вычисленные по этой зависимости значения y при заданных входах лучше всего аппроксимируют фактические значения выходов. Для определения формы математического описания в задачах идентификации используются методы регрессионного анализа.

Однако, как бы детально не изучалось поведение «черного ящик» нельзя вывести обоснованного суждения о его внутреннем устройстве, ибо одним и тем же поведением могут обладать различные объекты, а одно и то же соотношение между входами и выходами может в пределах имеющихся статистических данных удовлетворительно описываться несколькими различными математическими выражениями. Кроме того, применение метода «черного ящика» для описания функционирования сложных объектов с большим числом входов и выходов редко когда бывает удачным. Это связано с тем, что с увеличением числа факторов регрессионной модели обычно падает ее достоверность. Как показывает практика, удовлетворительные модели получаются при описании ситуации, в которой выходной фактор существенно связан не более чем с пятью-шестью входными факторами. Это обстоятельство определяет границы использования метода «черного ящика».

Как уже отмечалось выше, не во всех случаях возможно дать формализованное описание работы объекта как единого целого без разбивки его на отдельные элементы-модули.

При решении прямой задачи для каждого модуля, соответствующего элементарному процессу, проводится выбор метода математического описания, на базе которого будет строиться соответствующая модель поведения. Основой выбора метода математического описания является знание физической природы функционирования описываемого элемента, достаточно широкого круга экономико-математических методов, возможностей и особенностей ЭВМ, на которой планируется проведение моделирования. Так как для многих рассматриваемых явлений имеется достаточно удобное и проверенное практикой математическое описание, в первую очередь нужно обратиться к типовым математическим методам и схемам, использовать их для формализации и лишь при необходимости создавать оригинальные зависимости.

При развитой системе математического обеспечения ЭВМ, на которой предполагается проводить моделирование, целый ряд процедур может быть выполнен с помощью имеющихся стандартных средств. Если разработчик модели знает систему математического обеспечения конкретной ЭВМ, то это позволяет ему привести ряд модулей разрабатываемой модели к виду, позволяющему использовать стандартные программы или пакеты прикладных программ.

Оригинальные уравнения можно вывести в ходе обследования объекта, написать на основе предыдущих исследований подобных систем. Для построения математических моделей элементарных процессов, протекающих в соответствии с определенными законами, используются формульные выражения этих законов. Необходимые формулы берут либо из технической и научной литературы, либо выводят с помощью специально поставленных экспериментов. Статистические физические процессы обычно описываются алгебраическими уравнениями, а динамические – дифференциальными или конечно-разностными.

В итоге проведения формализации для каждого элементарного процесса-модуля создается его математическая модель. При разработке математических моделей элементарных процессов-модулей общей математической модели переменные в модели элементарного процесса обычно рассматриваются независимо от переменных в моделях других элементарных процессов, т.е. сначала разрабатываются частные модели. Только после окончания разработки проводиться стыковка их по ходам и выходам в единую математическую модель объекта. Совокупность математических моделей для отдельных модулей, рассматриваемых совместно, в общем случае не составляет математической модели для исследуемого процесса, а пока характеризует лишь отдельные изолированные элементы системы. Поэтому после формализации отдельных модулей производится их объединение в общую математическую модель, для чего в нее, если это необходимо, вводятся логические блоки, передающие управления от одного модуля к другому. Для этого логические условия формализуются в виде равенств или неравенств. Полученная совокупность соотношений явится описательной математической моделью исследуемого объекта. Формализация критерия оптимальности целевой функции переводит описательную модель в оптимизационную.

В самом общем виде многокритериальная оптимизационная математическая модель представляется соотношениями

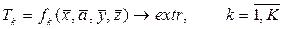(2.12)

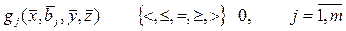. (2.13)

В оптимизационной математической модели, определяемой выражениями (2.12) и (2.13), выходные факторы объекта w_l модели (2.11) в записи не отражены, хотя, естественно, и критерий, и ряд ограничений определяются через эти характеристики. Множество входных факторов модели 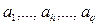и входных факторов ее отдельных модулей в записи модели (2.12) – (2.13) подразделяется на переменные объекта 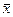, константы 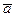и 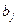, случайные 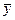и неопределенные 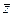факторы.