Установление качественных зависимостей

В состав ограничений решаемой задачи помимо внешних ограничений входят внутренние, выявленные или введенные входе уяснения задачи и выбора целей пределы, сужающие область осуществимых, приемлемых или допустимых решений и фиксирующие многие внутренние и внешние свойства модели объекта. Эти ограничения могут вводиться либо разработчиком модели (искусственные ограничения-допущения), либо определяться самим объектом вследствие присущих ему свойств (естественные ограничения). Ограничения первого типа, будучи субъективными, могут подвергаться изменениям. Вводя допущения, исследователь всегда стремиться выбрать рациональное соотношение между сложностью модели и затратами на ее разработку и ее соответствием исследуемому объекту. Ограничения второго типа, будучи субъективными, могут подвергаться изменениям. Вводя допущения, исследователь всегда стремится выбрать рациональное соотношение между сложностью модели и затратами на ее разработку и ее соответствием исследуемому объекту. Ограничения второго типа обусловлены объективными законами функционирования исследуемого объекта. К наиболее часто встречающимся естественным ограничениям относятся физические пределы на параметры объекта ( например, габариты, быстродействие и т.д.), ограничения из-за неполной совместимости элементов.

В модели ограничения представляют собой устанавливаемые пределы изменения значений переменных или иных факторов модели, условия распределения или расходования тех или иных средств (энергии, запасов, времени и т.п.). Так, например, ограничения на переменные состояния и переменные управления, состояния и переменных управления (жесткие ограничения), либо устанавливают дополнительные зависимости между переменными состояния и переменными управления. Жесткие ограничения устанавливают верхние (нижние) значения переделов, которые ни в коем случае не должны нарушаться. Нежесткие ограничения на переменные не запрещают превышение пределов ограничения. Обычно они учитывают путем добавления к целевой функции «штрафа», величина которого зависит от величины превышения ограничения.

Для всех установленных ограничений и критериев на основе совмещенного дерева целей-параметров записываются их качественные зависимости от параметров объектов и характеристик окружения. Эти взаимосвязи являются прообразом математической модели и отражают концепцию ее построения. Таким образом, совмещенное дерево целей-параметров является как бы скелетом математической модели.

Для иллюстрации запишем фрагмент концептуальной модели для совмещенного дерева целей-параметров, представленного на рис. 2.11:

;

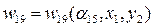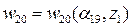
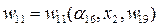
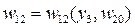
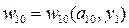
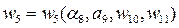
Анализ характера факторов внешней среды, содержания и числа критериев оптимальности помогает сформулировать будущую задачу принятия решения, например, однокритериальная детерминированная, однокритериальная стохастическая, однокритериальная с неопределенными факторами антагонистической природы, многокритериальная детерминированная и т.п., и наметить соответствующий метод принятия оптимального решения.

Выбором метода оптимального решения заканчивается формирование концептуальной модели объекта. Однако в ряде случаев после ее получения в целях упрощения целесообразно воспользоваться предельным анализом, заключающимся в оценке максимальных и минимальных величин составляющих критерий по области изменения параметров системы и характеристик окружения. Если величины отдельных составляющих на порядок и более превышают величины других составляющих, то исключение последних из критерия оптимальности приведет к незначительных погрешностям. Это позволит уменьшить число составляющих критерия оптимальности и сократить тем самым сложность математической модели. В результате проведения предельного анализа окончательно формируется структура критериев оптимальности и вся концептуальная модель в целом. Заключительным шагом создания концептуальной модели является оценка ее адекватности исследуемой ситуации.

С начала работы по формированию концептуальной модели разработчику целесообразно завести рабочий документ «Перечень допущений», в который будут заноситься все ограничения и допущения, принятые им на различных этапах построения и реализации модели. Эта информация будет крайне необходима как для принятия решения об адекватности концептуальной и математической модели, так и для правильной интерпретации результатов моделирования.