Процедура построения и реализации модели на ЭВМ

Процедуру построения модели и подготовки управленческого решения с помощью моделирования на ЭВМ можно представить состоящей из ряда этапов (рис. 1.5), хотя в конкретных случаях некоторые этапы могут опускаться, а ряд работ по построению модели – вестись параллельно.

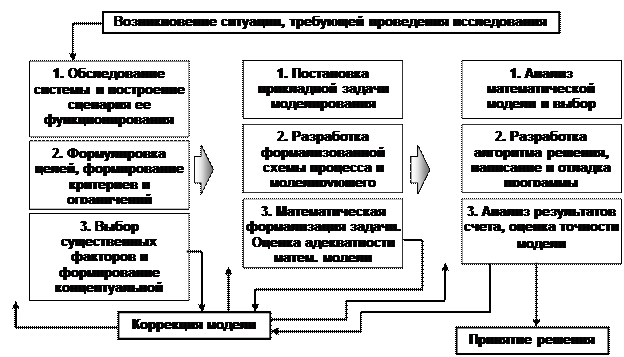
Рис. 1.5. Этапы построения и исследования математической модели

Содержательной основой для построения математической модели объекта является его концептуальная модель. Под концептуальной моделью объекта понимается совокупность качественных зависимостей критериев оптимальности и различного рода ограничений от факторов, существенных для отражения функционирования объекта. Концептуальная модель отражает следующие основные моменты:

условия функционирования объекта, определяемые характером взаимодействий между объектом и его окружением, между элементами объекта;

цели исследования объекта и направления улучшения его функционирования;

возможности управления объектом, определяющие состав управляемых переменных объекта.

В связи с этим при формулировке концептуальной модели объекта возникают проблемы:

составления упрощенного и в то же время адекватного поставленной цели описания исследуемой ситуации – сценария функционирования объекта;

формулировки и уточнения формулировки целей, стоящих перед объектом при его функционировании;

формализация целей в критерии оптимальности;

формализации внешних и внутренних ограничений;

выбора факторов, описывающих объект и его окружение, которые должны быть учтены в исследовании и соответственно включены в математическую модель;

классификации факторов и выделения из них в первую очередь управляемых переменных.

Построение концептуальной модели является важнейшим этапом моделирования, т.к. именно оно определяет направление, цели, область исследования. Заключительным шагом построения концептуальной модели является оценка ее адекватности исследуемой ситуации.

Следующим этапом является формирование на основе концептуальной модели математической модели объекта. Главная проблема этого этапа – определение количественных, математических соотношений, формализующих качественные зависимости концептуальной модели. Даже при наличии детально проработанного сценария эти соотношения могут быть неочевидны. В связи с этим зачастую возникает необходимость в выполнении промежуточного этапа между построением концептуальной и математической модели объекта – преобразования сценария в алгоритм, описывающий (моделирующий) взаимодействие элементов между собой и с окружением во времени.

Для реализации математической модели на ЭВМ она должна быть представлена численно, т.е. заданы числовые значения констант, диапазоны изменения неопределенных факторов и управляемых переменных, законы распределения случайных величин. При этом зачастую возникают проблемы эффективного представления числовой информации в математической модели для ее реализации на ЭВМ, например, сжатие табличной информации методами интерполяции, аппроксимации и экстраполяции, обработки статистических данных для получения формы и характеристик законов распределения случайных величин, получения эмпирических зависимостей между факторами модели и т.п. Заключительным шагом формирования математической модели является оценка ее адекватности по отношения к концептуальной модели.

Этап исследования математической модели начинается с ее анализа (отнесения к тому или иному классу) и выбора соответствующего метода ее решения. Главная проблема этого этапа – разработка алгоритма поиска решения на модели, действительно обеспечивающего поиск оптимального или наилучшего в заданных условиях решения в пределах времени счета ЭВМ.

И, наконец, заключительным этапом является оценка точности полученного на модели результата. Проблема оценки точности экономических моделей пока еще до конца не решена, разработаны лишь подходы к ее решению, на основе которых можно оценить погрешности результатов той или иной конкретной модели.

1.4. Математическое описание экономических
систем и явлений

Важным фактором, определяющим роль математики в различных приложениях, является возможность описания наиболее существенных черт и свойств изучаемого объекта на языке математических символов и соотношений. Такое описание принято называть математическим моделированием или формализацией.

Так как в литературе нет единого, строгого определение математической модели, то в качестве рабочего в этой книге будем принимать следующее определение.

Математической моделью реального объекта (явления) называется ее упрощенная, идеализированная схема, составленная с помощью математических символов и операций (соотношений).

Следовательно, для получения математической модели сначала вводится система буквенных обозначений элементов реального объекта и затем, на основе изучения существующих взаимосвязей между этими элементами, составляются отражающие их математические соотношения (уравнения, неравенства и др.).

Для чего составляется математическая модель, и какова ее роль в исследовании экономических задач?

Любое ответственное решение в экономике требует проведения эксперимента. Семь раз отмерь, один раз отрежь — так гласит основной принцип одного из разделов прикладной математики. При наличии математической модели мы избавляемся от необходимости дорогостоящих экспериментов, как правило, сопровождаемых многократными пробами и ошибками. Это можно делать на модели, которую, условно говоря, можно резать и перекраивать неоднократно без всяких капиталовложений. Это одно достоинство модели. Другое заключается в том, что формализация дает возможность сформулировать реальную задачу как математическую и позволяет воспользоваться для анализа универсальным и мощным математическим аппаратом, который не зависит от конкретной природы объекта. Математика проводит детальный количественный анализ модели, помогает предсказать, как поведет себя объект в различных условиях и дает рекомендации для выбора наилучших вариантов решения проблемы. Построение формальных моделей, их анализ и вывод практических рекомендаций – одна из важнейших задач прикладной математики.

Сложность экономических систем превышает порог, до которого стоится точная математическая теория. Поэтому неудивительно, что сколько-нибудь универсальных методов построения математических моделей в экономике не существует. Можно говорить лишь о некоторых общих принципах и требованиях к таким моделям. Перечислим наиболее основные из них:

1. адекватность (соответствие модели своему оригиналу),

2. объективность (соответствие научных выводов реальным условиям),

3. простота (не засоренность модели второстепенными факторами),

4. чувствительность (способность модели реагировать изменению начальных параметров),

5. устойчивость (малому возмущению исходных параметров должно соответствовать малое изменение решения задачи),

6. универсальность (широта области применения).

Комментируя первое свойство, можно заметить, что математическая модель нетождественна самому объекту, а является его приближенным отражением. Говоря об объективности, следует иметь в виду, что никакая отдельно взятая модель не может вполне правильно отразить все свойства сложной экономической действительности. Поэтому формализация экономической задачи проводится наряду с принятием некоторых предварительных условий, предположений, ограничений. Стремление к простоте модели продиктовано ограниченными возможностями вычислительной техники и экономии временных ресурсов при исследовании модели. Практическое значение модель приобретает тогда, когда ее изучение имеющимися средствами более доступно, чем изучение самого объекта. Требования чувствительности и устойчивости являются отражением объективных характеристик экономических процессов. Одна и та же математическая модель может применяться для исследования экономических задач различного содержания. Это свойство и называется универсальностью.

Разработка новой модели – это сложный творческий процесс, требующий больших умственных и временных затрат. Для экономии этих ресурсов полезно обращаться к существующему «банку» моделей для проверки пригодности их к новой задаче. Можно привести следующую схему выбора модели и метода ее исследования (рис. 1.6)

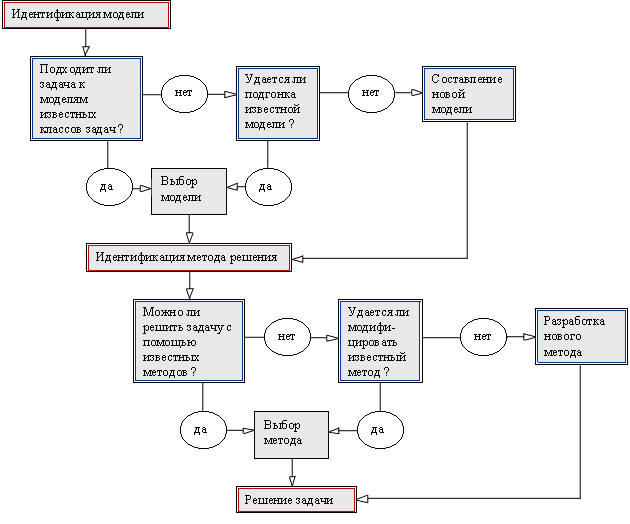
Рис. 1.6. Схема выбора модели и метода ее исследования.

Для того, чтобы математическая модель удовлетворяла всем тем требованиям, которые перечислены выше, необходимо тщательно изучить предметную область, собрать и проанализировать большой объем информации. Только в результате такого предварительного изучения самого объекта можно отличить цели от средств их достижения, следствия от причин их породивших, основные факторы от второстепенных.

В этой связи кратко охарактеризуем основные элементы экономики в целом, как объекта моделирования.

Первичными элементами экономики являются товары и участники. Говорят, что имеются экономические товары и участники экономики, если установлено, что эти товары обмениваются один на другой в результате соглашений, в которых заинтересованными сторонами выступают участники. То есть экономический товар – это именно то, что является предметом сделок в данном обществе – труд, капитал, ресурсы, продукты потребления, услуги, информация, ценные бумаги и т.д. Например, общественные посты, при продажности официальных учреждений, являются экономическими товарами. Становясь наследственными или замещаемыми по конкурсу, они перестают быть экономическими товарами. Следовательно, экономический товар определяется способностью к обмену.

Имеется один особый товар, являющийся эквивалентом при обмене – деньги. Деньги служат средством обращения, мерой стоимости, средством сбережения. Денежный эквивалент единицы товара называется его ценой.

Основными участниками экономики являются домашние хозяйства, фирмы и государство.

Домашние хозяйства, с одной стороны, являются потребителями конечного продукта, с другой - владельцами ресурсов (земельных, трудовых и др.). Продавая свои ресурсы домашние хозяйства получают доход, а также участвуют в распределении прибыли производственных предприятий (например, посредством ценных бумаг).

Фирмы, с одной стороны, являются производителями товаров и услуг, с другой – потребителями ресурсов. Фирмы получают доход от продажи своих товаров и услуг и являются владельцами производственных мощностей.

Государство выполняет важные законодательные, управленческие и регулирующие функции. С точки зрения движения товаров в экономике государство является как продавцом (государственных предприятий, природных ресурсов, ценных бумаг и др.), так и покупателем (государственных закупок продовольствия, вооружения, сырья и др.).

Таким образом, большинство участников экономики действует одновременно как покупатель и продавец. Взаимодействуя между собой, покупатели и продавцы образуют рынок. Основными рыночными понятиями являются спрос, предложение, конкуренция и цена.

Спрос можно определить как платежеспособную потребность в том или ином товаре. Спрос на товар зависит от его цены (т.е. спрос является функцией от цены). Как правило, при высокой цене приобретается меньшее количество товара (обратная связь (рис. 1.7 )). В экономике этот факт называется законом спроса.

Предложение – это то количество товара, которое производители могут и хотят произвести. Предложение также зависит от цены товара (прямая связь (рис. 1.7)). В экономике этот факт называется законом предложения.

Если вся масса товара, произведенная в расчете на данную цену, может быть по этой цене продана полностью, то говорят, что по данному виду товара в экономике существует равновесие. Иными словами, существует такая цена, для которой спрос на данный товар равен предложению. Такая цена называется равновесной (рис. 1.7 ).

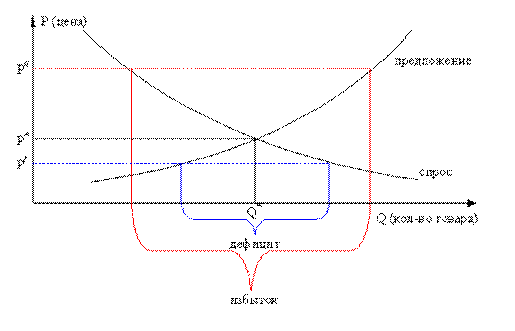
Рис.1.7. Кривая спроса и предложения и точка равновесия.

Если существует равновесие по всем товарам (и услугам), то говорят о экономическом равновесии. Равновесие —это то состояние к которому стремится экономика, так как в этом случае нет ни дефицита, ни избытка, т. е. удовлетворены интересы всех участников экономики. Возможность существования экономического равновесия находится в обратной зависимости от многообразия (видов) товаров. Чем больше видов, тем сложнее взаимосвязи между ними (например, очевидно, что спрос на чай зависит от наличия кофе, соков, молока и т. д.). Поэтому для получения реальных результатов в математических моделях рассматриваются только основные виды товаров (например, товары, составляющие потребительскую корзину).

Рынки можно классифицировать по различным признакам. В математических моделях часто применяется классификация по числу участников (рис. 1.8 ).

Рис. 1.8. Виды рынков (по числу участников)

В настоящее время можно говорить о том, что для каждого из перечисленных рынков существует своя математическая теория.

Примеры составления математических моделей

Пример 1.5.1.

Пусть некоторый экономический регион производит несколько (n) видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения на эти товары изучен. Надо определить годовой объем выпуска продуктов, с учетом того, что этот объем должен обеспечить как конечное, так и производственное потребление.

Составим математическую модель этой задачи. По ее условию даны: виды продуктов, спрос на них и технологический процесс; требуется найти объем выпуска каждого вида продукта.

Обозначим известные величины:

c_i – спрос населения на i-й продукт (i=1,...,n); a_ij – количество i-го продукта, необходимое для выпуска единицы j -го продукта по данной технологии ( i=1,...,n ; j=1,...,n);

Обозначим неизвестные величины:

х_i – объем выпуска i-го продукта (i=1,...,n); совокупность с=( c₁ ,...,c_n ) называется вектором спроса, числа a_ij – технологическими коэффициентами, а совокупность х =( х₁ ,...,х_n ) – вектором выпуска.

По условию задачи вектор храспределяется на две части: на конечное потребление (вектор с) и на воспроизводство (вектор х-с). Вычислим ту часть вектора хкоторая идет на воспроизводство. По нашим обозначениям для производства х_j количества j-го товара идет a_ij · х_j количества i-го товара.

Тогда сумма a_i1 · х₁ +...+ a_in · х_n показывает ту величину i-го товара, которая нужна для всего выпуска х =( х₁ ,...,х_n ).

Следовательно, должно выполняться равенство:

.

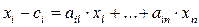Распространяя это рассуждение на все виды продуктов, приходим к искомой модели:

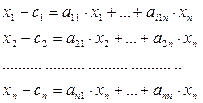
Решая эту систему из n линейных уравнений относительно х₁ ,...,х_n и найдем требуемый вектор выпуска.

Для того, чтобы написать эту модель в более компактной (векторной) форме, введем обозначения:

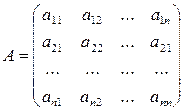
Квадратная ( 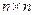) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х-с=Ах или

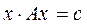(1.6)

Мы получили классическую модель «Затраты – выпуск», автором которой является известный американский экономист В. Леонтьев.

Пример 1.5.2.

Нефтеперерабатывающий завод располагает двумя сортами нефти: сортом А в количестве 10 единиц, сортом В — 15 единиц. При переработке из нефти получаются два материала: бензин (обозначим Б) и мазут (М). Имеется три варианта технологического процесса переработки:

I: 1ед.А + 2ед.В дает 3ед.Б + 2ед.М

II: 2ед.А + 1ед.В дает 1ед.Б + 5ед.М

III: 2ед.А + 2ед.В дает 1ед.Б + 2ед.М

Цена бензина — 10 долл. за единицу, мазута — 1 долл. за единицу.

Требуется определить наиболее выгодное сочетание технологических процессов переработки имеющегося количества нефти.

Перед моделированием уточним следующие моменты. Из условия задачи следует, что «выгодность» технологического процесса для завода следует понимать в смысле получения максимального дохода от реализации своей готовой продукции (бензина и мазута). В связи с этим понятно, что «выбор (принятие) решения» завода состоит в определении того, какую технологию и сколько раз применить. Очевидно, что таких возможных вариантов достаточно много.

Обозначим неизвестные величины:

х_i – количество использования i-го технологического процесса (i=1,2,3).
Остальные параметры модели (запасы сортов нефти, цены бензина и мазута) известны.

Теперь одно конкретное решение завода сводится к выбору одного вектора х=( х₁ ,х₂ ,х₃), для которого выручка завода равна (32х₁+15х₂ +12х₃) долл. Здесь 32 долл. – это доход, полученный от одного применения первого технологического процесса (10 долл. ·3ед.Б + 1 долл. ·2ед.М = 32 долл.). Аналогичный смысл имеют коэффициенты 15 и 12 для второго и третьего технологических процессов соответственно. Учет запаса нефти приводит к следующим условиям:

для сорта А: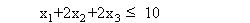

для сорта В: ,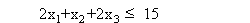

где в первом неравенстве коэффициенты 1, 2, 2 – это нормы расхода нефти сорта А для одноразового применения технологических процессов I, II, III соответственно. Коэффициенты второго неравенства имеют аналогичный смысл для нефти сорта В.

Математическая модель в целом имеет вид:

Найти такой вектор х = ( х₁ ,х₂ ,х₃), чтобы максимизировать

f(x) =32х₁+15х₂ +12х₃

при выполнении условий:

.

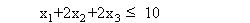
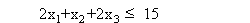
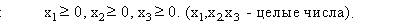Сокращенная форма этой записи такова:

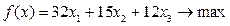
при ограничениях

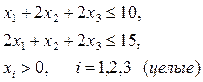(1.7)

Мы получили так называемую задачу линейного программирования.

Модель (1.7.) является примером оптимизационной модели детерминированного типа (с вполне определенными элементами).

Пример1.5.3.

Инвестору требуется определить наилучший набор из акций, облигаций и других ценных бумаг для приобретения их на некоторую сумму с целью получения определенной прибыли с минимальным риском для себя. Прибыль на каждый доллар, вложенный в ценную бумагу j - го вида, характеризуется двумя показателями: ожидаемой прибылью и фактической прибылью. Для инвестора желательно, чтобы ожидаемая прибыль на один доллар вложений была для всего набора ценных бумаг не ниже заданной величины b.

Заметим, что для правильного моделирования этой задачи от математика требуются определенные базовые знания в области портфельной теории ценных бумаг.

Обозначим известные параметры задачи:

n – число разновидностей ценных бумаг; а_j – фактическая прибыль (случайное число) от j-го вида ценной бумаги ; 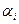– ожидаемая прибыль от j-го вида ценной бумаги.

Обозначим неизвестные величины:

y_j — средства, выделенные для приобретения ценных бумаг вида j.

По нашим обозначениям вся инвестированная сумма выражается как .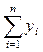
Для упрощения модели введем новые величины

.

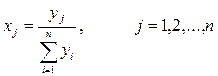Таким образом, х_i — это доля от всех средств, выделяемая для приобретения ценных бумаг вида j.

Ясно, что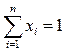

Из условия задачи видно, что цель инвестора — достижение определенного уровня прибыли с минимальным риском. Содержательно риск — это мера отклонения фактической прибыли от ожидаемой. Поэтому его можно отождествить с ковариацией 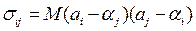прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.

Математическая модель исходной задачи имеет вид:

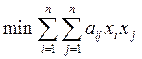
при ограничениях

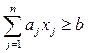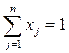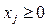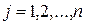, , , . (1.8)

Мы получили известную модель Марковица для оптимизации структуры портфеля ценных бумаг.

Модель (1.8.) является примеров оптимизационной модели стохастического типа (с элементами случайности).

Пример1.5.4.

На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль р_j , если же он не будет пользоваться спросом - убыток q_j .

Перед моделированием обсудим некоторые принципиальные моменты. В данной задаче лицом, принимающим решение (ЛПР), является магазин. Однако исход (получение максимальной прибыли) зависит не только от его решения, но и от того, будет ли завезенный товар пользоваться спросом, т. е. будет ли выкуплен населением (предполагается, что по какой-то причине у магазина нет возможности изучить спрос населения). Поэтому население может рассматриваться как второе ЛПР, выбирающее тип товара согласно своего предпочтения. Наихудшим для магазина «решением» населения является: «завезенный товар не пользуется спросом». Так что, для учета всевозможных ситуаций, магазину нужно считать население своим «противником» (условно), преследующим противоположную цель – минимизировать прибыль магазина.

Итак, имеем задачу принятия решения с двумя участниками, преследующими противоположные цели. Уточним, что магазин выбирает один из типов товаров для продажи (всего n вариантов решений), а население — один из типов товаров, который пользуется наибольшим спросом (n вариантов решений).

Для составления математической модели нарисуем таблицу с n строками и n столбцами (всего n² клеток) и условимся, что строки соответствуют выбору магазина, а столбики — выбору населения. Тогда клетка (i, j) соответствует той ситуации, когда магазин выбирает i-й тип товара (i-ю строку), а население выбирает j-й тип товара (j-ю столбик). В каждую клетку запишем числовую оценку (прибыль или убыток) соответствующей ситуации с точки зрения магазина:

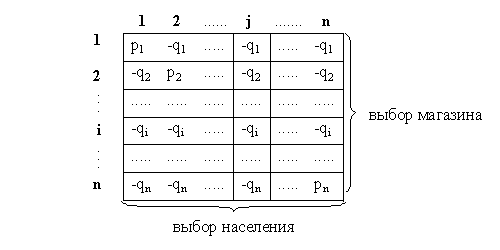
Числа q_i написаны с минусом для отражения убытка магазина; в каждой ситуации «выигрыш» населения (условно) равен «выигрышу» магазина, взятому с обратным знаком.

Сокращенный вид этой модели таков:

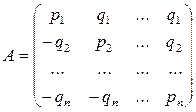(1.9)

Мы получили так называемую матричную игру. Модель (1.9.) является примером игровых моделей принятия решения.