Теоретической и прикладной механики

Кафедра

Теоретической и прикладной механики

Прикладная механика.

Часть первая.

Методические указания

для студентов факультета заочного обучения

Иваново 2005

Составители: Н.В. МАЛИНИНА

Ю.Е. ФИЛАТОВ

В.И. ШАПИН

Редактор Ю.Е. ФИЛАТОВ

Методические указания предназначены для студентов факультета заочного обучения ИГЭУ

Утверждены цикловой методической комиссией электромеханического факультета

Рецензент

кафедра теоретической и прикладной механики Ивановского государственного энергетического университета

Содержание

	Введение…………………………………………….
1.	Основы теории сопротивления материалов………
2.	Определение положения опасных сечений конструкций……………………………………………….
3.	Условия прочности и жесткости…………………..
4.	Расчёты на прочность и жесткость при центральном растяжении и сжатии…………………………
5.	Сдвиг и кручение. Расчёты на прочность и жёсткость при кручении…………………………………
6.	Изгиб.Расчёты на прочность и жесткость при прямом изгибе………………………………………
7.	Напряженное и деформированное состояние в точке…………………………………………………
	Библиографический список………………………..
	Приложение 1. Задачи к контрольной работе…….
	Приложение 2. Таблицы сортаментов…………….

ВВЕДЕНИЕ

Курс «Прикладная механика» является комплексной общеинженерной дисциплиной. Основные задачи – изучение основ прочности и освоение расчетов на прочность и жесткость простых силовых элементов несущих конструкций, освоение общих принципов построения машин, механизмов, деталей и их проектирования, ознакомление с основами стандартизации и взаимозаменяемости.

Курс «Прикладная механика» состоит из двух частей:

1- сопротивление материалов;

2- теория механизмов и деталей машин.

Данные методические указания предназначены для изучения первой части курса «Сопротивление материалов».

В результате изучения курса студент должен не только знать основные положения сопротивления материалов, теории механизмов и деталей машин, но и уметь выполнять необходимые расчеты и конструктивные разработки современных машин, способствующие улучшению производственных процессов с использованием различных средств механизации и автоматизации.

Данный курс основан на общенаучных дисциплинах (математике, вычислительной технике, теоретической механике, инженерной графике, материаловедении и т. д.) и он полностью используется в последующих специальных дисциплинах, изучающих машины, аппараты и другое оборудование с учетом специализации.

Контрольная работа включает 3 задачи. Задача контрольной работы содержит 10 вариантов. Для выполнения обязателен тот тип задания, который соответствует последней цифре шифра студента, и тот вариант этого типа, который соответствует предпоследней цифре шифра.

Например,студент имеющий шифр 184893,должен выполнить контрольную задачу, соответствующую третьему типу варианта №9.Если последняя цифра шрифта - нуль, то ему соответствуют задачи десятого типа. Если предпоследняя цифра нуль, то студент должен выполнить задачу варианта №10 своего типа.

ОСНОВЫ ТЕОРИИ СОПРОТИВЛЕНИЯ

МАТЕРИАЛОВ

Сопротивление материалов – это наука об инженерных методах расчета отдельных элементов конструкций на прочность и жесткость.

Конструкция считается прочной, если размеры каждого ее элемента подобраны так, что способны воспринимать заданную нагрузку, не разрушаясь, с учетом требуемого времени работы. Жесткость конструкции обеспечивается, если под действием заданной нагрузки деформации не превышают допускаемые пределы.

Использование указанных методов расчета должно обеспечивать надежность работы конструкции и сочетаться с принципом экономичности ее изготовления и эксплуатации.

В сопротивлении материалов рассматривают типичные элементы конструкций: стержень, пластину, оболочку(рис.1). Внешние нагрузки, действующие на элементы сооружений, подразделяют на сосредоточенные и распределенные, статические и динамические. Все реальные силы – это силы, распределенные по некоторой площади или объему. Однако распределенную нагрузку на небольшой площади, размеры которой очень малы по сравнению с размерами всего элемента, можно заменить сосредоточенной равнодействующей силой, что упростит расчет. Распределенные нагрузки имеют размерность единицы силы, отнесенной к единице длины или к единице поверхности или объема.

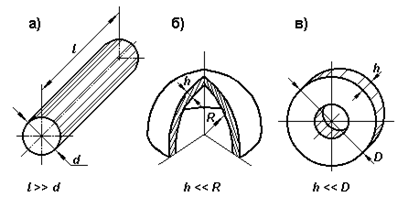
Рис 1. Модели формы конструкций:

а – стержень, б – оболочка, в – пластина

Статическими нагрузками считают те, которые нагружают конструкции постепенно, и, будучи приложены к сооружению, они не меняются или меняются во времени незначительно. При действии статических нагрузок на конструкцию все ее части находятся в равновесии; ускорения элементов конструкции отсутствуют или настолько малы, что ими можно пренебречь. Если же эти ускорения значительны, т. е. изменение скорости движения элементов машины происходит за сравнительно небольшой период времени, то мы имеем дело с приложением динамических нагрузок. Примерами таких нагрузок могут служить внезапно приложенные нагрузки, ударные и повторно-переменные. Действие таких нагрузок сопровождается возникновением колебаний конструкций или сооружений. Вследствие изменения скорости колеблющихся масс возникают силы инерции, пропорциональные (согласно второму закону Ньютона) колеблющимся массам и ускорениям.

Методы расчета элементов конструкций излагаются на основе следующих упрощений и допущений: материал тела имеет сплошное (непрерывное) строение, т. е. не принимается во внимание дискретная атомарная структура вещества; принимается, что материал тела однороден, т. е. обладает во всех точках одинаковыми свойствами; материал тела изотропен, когда он обладает во всех направлениях одинаковыми свойствами; предполагается, что в теле до приложения нагрузки нет внутренних (начальных) усилий; что результат действия на тело системы сил равен сумме результатов действия тех же сил, прилагаемых к телу последовательно и в любом порядке.

Для лучшего усвоения пройденного материала после изучения каждой темы необходимо ответить на вопросы для самопроверки, приведенные в методических указаниях.

В природе различают упругое и упругопластичное твердые тела. Упругое тело после снятия внешней нагрузки восстанавливает свои первоначальные размеры и форму. В этом случае деформация тела называется упругой. Упругопластичное тело восстанавливает свои первоначальные размеры и формы не полностью, т. е. имеет место остаточная деформация. В строительных сооружениях и машинах недопустимо появление остаточных деформаций.

От действия внешних нагрузок в поперечных сечениях возникают внутренние силовые факторы, которые определяют, используя метод сечений. Твердое тело, находящееся под действием внешних нагрузок, мысленно рассекают на две части и рассматривают равновесие одной из частей. Действие отброшенной части на оставшуюся заменяют внутренними нагрузками, приложенными в рассматриваемом сечении. Составляя уравнения равновесия оставшейся части тела, нагруженного внешними и внутренними силовыми факторами, находят последние.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ

ОПАСНЫХ СЕЧЕНИЙ КОНСТРУКЦИЙ

Известно [6], что различают усилия внешние и внутренние. Внешние усилия (нагрузки) – это количественная мера механического взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия – это количественная мера механического взаимодействия двух частей одного тела, расположенных по разные стороны сечения, и вызванное действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.

На рис.2,а приведена расчетная схема бруса с произвольной комбинацией внешних усилий, но образующих равновесную систему усилий:

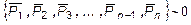. (1)

При этом реакции связей определяются из известных уравнений равновесия (статики) твердого тела [6]:

; ;

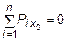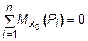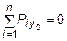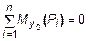; ; (2)

; ,

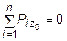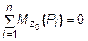гдех₀ , у₀ , z₀– базовая система координатных осей.

Мысленное разрезание бруса на две части произвольным сечением А (рис.2,а) требует выполнения условия равновесия для каждой из двух отсеченных частей (рис.2,б; 2,в). Здесь, как известно [1 – 4], {S′ } и {S" } – это внутренние усилия, возникающие соответственно в левой и правой отсеченных частях вследствие действия внешних усилий. Причем, при соединении мысленно отсеченных частей, условие равновесия тела обеспечивается соотношением

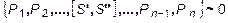. (1а)

Так как исходная система внешних сил (1) эквивалентна нулю, получаем:

{S^′} = – {S^″} . (3)

Это условие соответствует четвертой аксиоме статики о равенстве сил действия и противодействия. Используя общую методологию теоремыПуансо [6] о приведении произвольной системы сил к заданному центру и выбрав за полюс приведения сил центр масс сечения А' точку С'(рис.3,б), систему внутренних усилий для левой части {S' } сводим к главному вектору 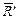и главному моменту 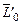внутренних усилий. Аналогичное приведение делается для правой отсеченной части, где положение центра масс сечения А″ определяется, соответственно, точкой С" (рис.2,в).

{ S′ } ~ { R′, L′₀ }; { S" } ~ { R", L"₀ }. (4)

Здесь в соответствии с четвертой аксиомой статики по-прежнему имеют место следующие соотношения:

R′= –R",L′₀ = –L"₀. (5)

Таким образом, главный вектор и главный момент системы внутренних усилий, возникающие в левой условно отсеченной части бруса, равны по величине и противоположны по направлению главному вектору и главному моменту системы внутренних усилий, возникающим в правой условно отсеченной части.

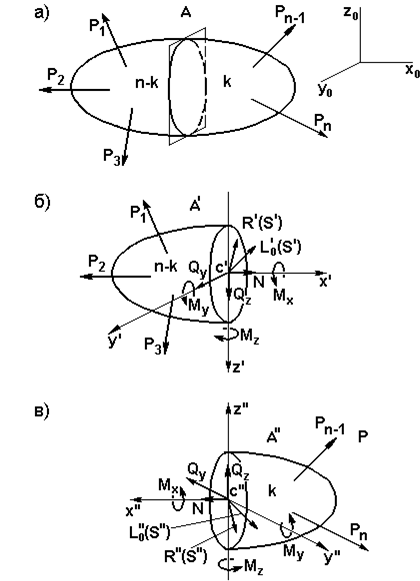
Рис. 2. Метод сечений:

а – расчетная схема бруса, б – левая отсеченная часть, в – правая отсеченная часть

График (эпюра) распределения численных значений главного вектора и главного момента вдоль продольной оси бруса и предопределяют, прежде всего, конкретное решение задач обеспечения прочности, жесткости и надежности конструкций.

Определим способ нахождения компонент внутренних усилий, которые характеризуют простые виды сопротивлений: растяжение-сжатие, сдвиг, кручение и изгиб.

В центрах масс исследуемых сечений С' или С" зададимся соответственно левой (с', х', у', z') или правой (с", х", у", z²)СИСТЕМАМИ координатных осей (рис.2,б; 2,в), которые, в отличие от базовой системы координат x₀ , у₀ , z₀ , будем называть “следящими”. Термин обусловлен их функциональным назначением. А именно: отслеживание изменения положения сечения А (рис.2,а) при условном смещении его вдоль продольной оси бруса, например при: 0 ≤ х¢₁ ≤ а , а ≤ x¢₂ ≤ b и т.д., где 0, а и b – линейные координаты границ исследуемых участков бруса.

Спроектируем главный вектор 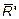или 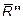и главный момент 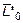или 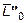на оси следящей системы координат (рис.2,б; 2,в):

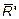{N', Q'_y , Q'_z} ; 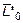{M'_x , M'_y , M'_z} ; (6)

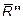{N", Q"_y , Q"_z}; 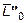{M"_x , M"_y , M"_z} .

Эти проекции называются:

N – нормальная или продольная сила, возникает при центральном растяжении или сжатии;

М_x– внутренний крутящий момент, возникает при кручении;

Q_z , Q_у – поперечные или перерезывающие силы, возникают при сдвиговых деформациях;

М_у ,М_z – внутренние изгибающие моменты, соответствуют изгибу.

При этом знак проекций главного вектора и главного момента внутренних усилий на оси следящей системы координат соответствуют правилам статики (в теоретической механике). Сила положительна, если ориентирована вдоль положительного направления оси. Момент положителен, если направлен против часовой стрелки, при наблюдении со стороны конца оси.

Общее число внутренних усилий в статически определимых задачах – шесть – совпадает с количеством уравнений равновесия для пространственной системы сил и связано с числом возможных взаимных перемещений одной условно отсеченной части тела по отношению к другой. Эти перемещения могут наблюдаться при разрушении тела по этому сечению.

Соединение левой и правой мысленно отсеченных частей бруса дает систему внешних и внутренних усилий, которая с учетом равновесия каждой отсеченной части имеет вид:

{P₁, P₂, P₃, … , N', N", Q'_y, Q"_y, Q'_z, Q"_z, M'_x, M"_x,

M'_y, M"_y, M'_z, M"_z, … , P_n-1, P_n} ~ 0 . (7)

Анализ соотношения с учетом эквивалентности нулю исходной системы сил (1) дает:

{N', N", Q'_y, Q"_y, Q'_z, Q"_z, М'_x, M"_x,

M'_y, M"_y, М'_z, M"_z}~0 (8)

Полученное условие, как естественное следствие из соотношений (3), (4), (5), приводит к необходимости образования одноименными компонентами внутренних усилий попарно подсистем эквивалентных нулю. То есть приходим к известному принципу равенства по модулю и противоположной направленности всех одноименных компонент внутренних усилий.

1){N', N"} ~ 0 → N' = – N" ;

2) {Q'_y, Q"_y} ~ 0 → Q'_y = – Q"_y ;

3) {Q'_z, Q"_z} ~ 0 → Q'_z = – Q"_z. ; (9)

4) {М'_x, M"_x} ~ 0 → М'_x = – M"_x ;

5) {M'_y, M"_y} ~ 0 → M'_y = – M"_y ;

6) {М'_z, M"_z} ~ 0 → М'_z = – M"_z .

Искомые усилия определяют из соответствующих уравнений равновесия для любой из отсеченных частей, которые в следящей системе координатных осей приобретают вид:

1) 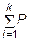_ix =N + P_1x+ P_2x + … + P_kx = 0 → N ;

2) 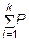_iy = Q_y + P_1y + P_2y + … + P_ky = 0 → Q_y ;

3) 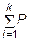_iz = Q_z + P_1z + P_2z + … + P_kz = 0 → Q_z ;(10)

4) 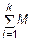_x (P_i) = M_x + M_x(P_i) + … + M_x(P_k) = 0 → M_x ;

5) 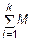_y (P_i) = M_y + M_y(P_i) + … + M_y(P_k) = 0 → M_y ;

6) 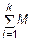_z (P_i) = M_z + M_z(P_i) + … + M_z(P_k) = 0 → M_z .

Здесь для простоты обозначений системы координат с' х' у' z' и с" х" у" z" заменены единой c x у z.

Таким образом, метод построения эпюр внутренних усилий (в редакции освобождающей от механического запоминания правил знаков для внутренних усилий) включает этапы:

1. Определить реакции в связях по величине и направлению в базовой системе координат.

2. Определить количество участков бруса для использования метода сечений.

3. Мысленно разрезать брус в пределах исследуемого участка.

4. Изобразить по желанию левую или правую условно отсеченную часть.

5. Указать пределы изменения положения сечения (центра масс) вдоль продольной оси в базовой системе координат на этом участке.

6. Ввести в рассматриваемом сечении соответственно левую или правую следящую систему координатных осей.

7. Указать внутренние усилия (заменяющие действие условно отброшенной части бруса на рассматриваемую часть), взяв их положительными по направлению (в следящей системе координат).

8. Составить уравнения равновесия для рассматриваемой условно отсеченной части бруса в следящей системе координат.

9. Выразить из уравнений равновесия искомые внутренние усилия.

10. Вычислить значения искомых внутренних усилий на границах участков и, при необходимости, – их экстремальные значения.

11. Выбрав масштаб усилий, выполнить построение эпюры в соответствие с полученными их абсолютными значениями и знаками.

Указанная последовательность действий (кроме п.1) составляет суть метода сечений (разреза), единственного для определения внутренних усилий. В нем этапы 3,4,7 и 8 являются ключевыми. Естественно, что все способы контроля достоверности нахождения искомых внутренних усилий сохраняются: по замкнутости векторных многоугольников сил и моментов как свидетельства равновесия, свойств функций и их производных при исследовании изгиба и т.д. [1,3,4].

При наличии распределенной нагрузки в соответствие с теоремойВариньона [6] векторный момент равнодействующей распределенной системы сил относительно любой точки равен сумме векторных моментов всех составляющих сил этой системы относительно той же точки.

Эпюра внутренних усилий позволяет достаточно просто, визуально найти положение опасного сечения, где действуют наибольшие по модулю внутренние усилия. В этом сечении наиболее вероятно разрушение конструкции при предельных нагрузках.

Схема нагружения.

Центральным растяжением или сжатием называют такой вид простого нагружения, при котором внешние силы направлены вдоль продольной оси бруса, а их точки приложения совпадают с центром массы сечений.

Внутренние усилия.

В поперечных сечениях бруса возникает только нормаль-ная (продольная) сила N, которая в произвольном поперечном сечении численно равна алгебраической сумме проекций на его продольную ось х всех внешних сил, приложенных по одну сторону от рассматриваемого сечения (10.1).

Между интенсивностью внешней продольной силы q и внутренней нормальной силой N имеется соотношение

dN(x)/dx = q(x). (18)

Из геометрического смысла производной (первая производная равна тангенсу угла между касательной к кривой и осью абсцисс) следуют правила для проверки соответствия эпюры нормальной силы расчетной схеме:

1. Если на участке отсутствует распределенная нагрузка (q=0), то нормальная сила постоянна.

2. Если на участке имеется равномерно распределенная нагрузка, то нормальная сила изменяется по линейному закону.

3. В сечении, где приложена внешняя сосредоточенная сила, эпюра N имеет скачок на величину этой силы.

4. Эпюра должна выходить из нуля и уходить в нуль (вне твердого тела внутренней силы нет).

Напряжения.

Нормальные напряжения s в поперечном сечении бруса, как интенсивность действия нормальной силы по сечению, в соответствии с гипотезой плоских сечений распределены равномерно (рис.4) и поэтому

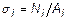, (19)

где i – номер участка с соответствующей нормальной силой N и площадью сечения А.

Условие прочности

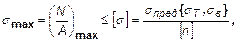(20)

где [ 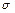] или 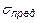, зависящие от материала, берутся по справочникам.

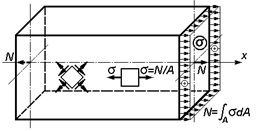Рис. 4. Эпюра нормальных напряжений в поперечном сечении и напряжения в наклонных сечениях при центральном растяжении

Перемещения.

Расчет абсолютного удлинения (укорочения) бруса ведется по закону Гука по участкам:

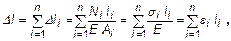(21)

где Е – модуль продольной упругости (модуль упругости 1 рода или модуль Юнга), e - относительное удлинение.

Если изменяется вдоль оси бруса площадь сечения или внутренние усилия, то

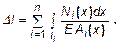(22)

Закон Гука верен только при упругих деформациях, когда напряжения не превышают предела пропорциональности.

При расчетах на растяжение нормальная сила, нормальное напряжение и перемещение (удлинение) положительны. Здесь знак имеет физический смысл, так как за пределом текучести σ_т поведение пластичных материалов и конструкций из них при растяжении и сжатии различается, а для хрупких материалов пределы прочности σ_в и соответственно допускаемые напряжения [σ] при растяжении меньше, чем при сжатии.

Пример 1.

Для заданной расчетной схемы (рис5,а) ступенчатого бруса оценить прочность конструкции и определить абсолютное удлинение. Брус имеет по длине три участка.

1. Реакция опоры.

Определяется из суммы проекций сил на ось х (10,1):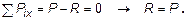

2. Внутренние усилия.

Эпюра внутренних усилий строится с применением метода сечений (рис. 2). Рассмотрим первый участок.

Задаваясь нормальной силой N, положительной по направлению, получим

.

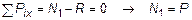Аналогично вычисляется нормальная сила и на других участках. В данном примере

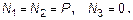
На рисунке 5,в приведена эпюра нормальных сил.

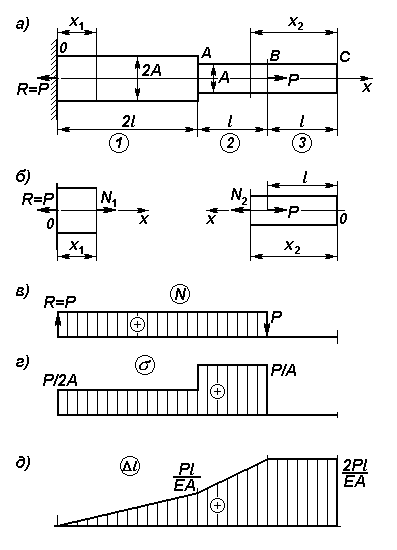
Рис. 5. Центральное растяжение–сжатие (к примеру 1):

а – расчетная схема; б – рассматриваемые отсеченные части;

в – эпюра нормальных сил; г – эпюра нормальных напряжений;

д – эпюра продольных перемещений

3. Напряжения.

Расчет нормальных напряжений в поперечном сечении бруса ведется по формуле (19). Для рассматриваемого примера получим:

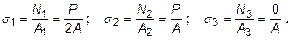
Эпюра нормальных напряжений приведена на рис. 5,г.

Для оценки прочности при проверочном расчете величина максимального напряжения сравнивается с допускаемым напряжением: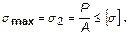

Величина перегрузки 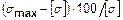в расчете по допускаемым напряжениям не должна превышать 5%.

Условие прочности позволяет также определять допустимую грузоподъемность системы:

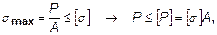
а также оптимальные размеры поперечного сечения (проектный расчет):

.

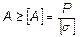4. Продольные перемещения.

Расчет удлинения бруса производится по закону Гука (21). Для рассматриваемого примера перемещение сечения А относительно 0 равно удлинению первого участка:

.

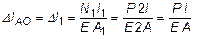Аналогично перемещение сечения В: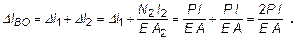

Полное удлинение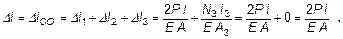

Эпюра перемещений приведена на рис. 5,д.

Характерно, что результат Δl_СВ = Δl₃ = 0 не означает абсолютной неподвижности сечений на участке 3, они перемещаются относительно сечения 0 (сечения заделки).

Эпюры усилий, напряжений и перемещений могут быть определены или проверены достаточно оперативно, используя прием векторного замыкания эпюры N (рис. 5,в) и с использованием геометрического смысла (по площади) соотношения (19). А именно

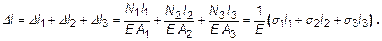Здесь σ_i×l_i – площади участков эпюры нормальных напряжений.

Вопросы для самопроверки

1. Какие тела называют упругими и упругопластичными? 2. В чем сущность метода сечений? 3. Что называют напряжением в данной точке сечения? 4. Какие напряжения называют нормальными? 5. Какие деформации являются упругими, а какие остаточными (пластическими)? 6. Как формулируется закон Гука? 7. Как определяют допустимые напряжения? 8. Что называют коэффициентом запаса прочности? 9. Каково условие прочности при растяжении? 10. Что называют пределом прочности и пределом текучести материала? 11. Что называют относительным остаточным удлинением при разрыве? 12. Что называют коэффициентом Пуассона и чему он равен? 13. Какие материалы называют хрупкими, а какие пластичными? 14. Как строится диаграмма растяжения?

И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ

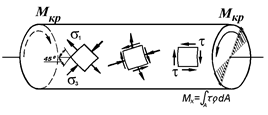
Сдвигом называют такой вид напряженного состояния, когда на гранях элемента действуют только касательные напряжения. Деформации, возникающие при сдвиге, называют угловыми деформациями или углом сдвига.

Схема нагружения.

Кручением называют такой вид простого нагружения, при котором внешние пары сил действуют в плоскостях поперечных сечений. Стержень, работающий на кручение, называют валом.

Внутренние усилия.

В поперечных сечениях вала возникает только крутящий момент М_х., который в произвольном поперечном сечении численно равен алгебраической сумме всех внешних моментов, приложенных по одну сторону от рассматриваемого сечения и вращающих вокруг продольной оси х.

Между интенсивностью внешнего скручивающего момента m и внутреннего крутящего момента M имеется соотношение

m(x) = dM(x)/dx, (23)

Из геометрического смысла производной (первая производная равна тангенсу угла между касательной к кривой и осью

Рис. 6 Эпюра касательных напряжений в поперечном сечении и напряжения в наклонных сечениях при кручении

абсцисс) следуют правила для проверки соответствия эпюры крутящих моментов расчетной схеме такие же, как для растяжения.

Напряжения.

При кручении круглого бруса в поперечных сечениях действуют и подлежат определению касательные напряжения, меняющиеся вдоль радиуса по линейному закону:

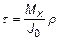. (24)

Здесь M_х – внутренний крутящий момент в сечении вала, ρ – полярная координата произвольной точки в поперечном сечении, J₀ – полярный момент инерции сечения. (Таким образом, в записи формулы использована полярная система координат.)

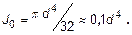
Наиболее опасными точками сечения вала, в которых действуют наибольшие касательные напряжения, являются точки около наружной поверхности (на контуре сечения), где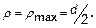

Следовательно,

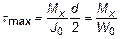, (25)

где W₀ – полярный момент сопротивления сечения.

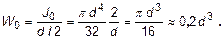
Для кольцевого профиля (труба) снаружным диаметром Dивнутренним d соответствующие характеристики имеют вид

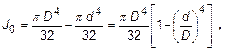
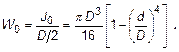
Условие прочности вала имеет вид

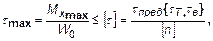(26)

где[t] – допускаемое касательное напряжение, которое определяется аналогично допускаемому нормальному напряжению или приближенно [t] ≈ (0.5 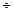0.6)[σ].

Если необходимо определить диаметр вала из условия прочности (26), то решение проводится относительно момента сопротивления:

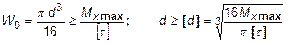. (27)

Перемещения.

Определение полного угла закручивания вала или угла поворота сечения вокруг продольной оси х проводят по закону Гука при кручении:

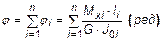, (28)

где G (МПа) – модуль упругости материала второго рода (модуль сдвига, модуль Стокса), i – номер участка.

Для валов с переменными параметрами перемещения вычисляются по формуле

.

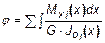При расчете валов наряду с выполнением условия прочности может потребоваться выполнение условия жесткости. Условие жесткости заключается в том, что максимальный относительный угол закручивания θ_max, то есть угол приходящийся на единицу длины вала, не должен превышать допустимых значений [θ].

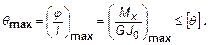(29)

Допустимый относительный угол закручивания устанавливается техническими условиями. Его величина для разных энергетических конструкций и различных режимов работы вала колеблется в достаточно широких пределах:

.

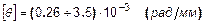По условию жесткости возможно решение тех же трех вариантов задач, что и по условию прочности.

Расчетное соотношение для определения диаметра вала из условия жесткости приобретает вид:

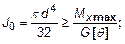
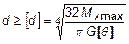. (30)

При расчете бруса на прочность (27) и жесткость (30) из двух найденных значений диаметра следует принять то, которое удовлетворяет обоим условиям надежности, то есть большее.

Диаметры вала в местах посадки на него различных деталей (дисков, шкивов, подшипников и т.п.) округляют до ближайшего стандартного значения.

Пример 2.

Для заданного вала (рис. 7,а), нагруженного скручивающими сосредоточенными и распределенными моментами, выполнить расчет на прочность и жесткость. Здесь принято М =m l.

1. Реактивный момент.

Вычисляется из уравнения равновесия – по условию равенства нулю суммы моментов относительно оси вращения (10,4):

→

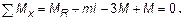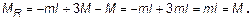
2. Внутренние усилия.

Вал имеет два участка. Следовательно, для построения эпюры внутренних крутящих моментов достаточно два раза применить метод сечений.

Для первого сечения (рис.7,б) для левой части вала уравнение равновесия имеет вид

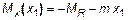
(на эпюре наклонная прямая).

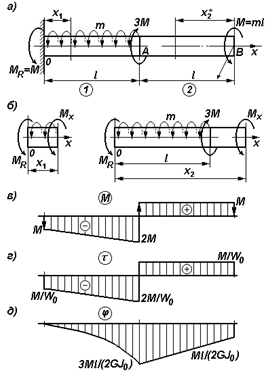
Рис. 7. Кручение (к примеру 2):

а – расчетная схема; б – рассматриваемые отсеченные части;

в – эпюра крутящих моментов; г – эпюра касательных напряжений;

д – эпюра угловых перемещений

На первом участке границы изменения x₁: 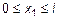. Подставляя эти значения, определяют величины моментов на границах участка:

,

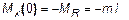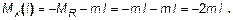
Аналогично на втором участке (для левой части вала) 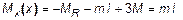= const ,

или (для правой части вала) .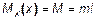

Эпюра внутренних крутящих моментов приведена на рис.7,в. Согласно указанным ранее правилам на первом участке она ограничена наклонной прямой, а на втором – прямой параллельной оси.

Из эпюры видно, что максимальное значение момента |M_max| =2M (а не 3M). Именно для этого опасного значения и проводится последующий расчет на прочность.

3. Касательные напряжения.

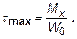
В рассматриваемом примере эпюра максимальных касательных напряжений (рис. 7,г) качественно повторяет эпюру моментов M_x (рис. 7,в), так как вал имеет постоянное сечение по

длине. Условие прочности проверяется для опасного сечения, которое находится на границе между участками:

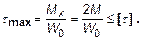
Если взять не сплошное, а кольцевое сечение, то при сохранении прежнего значения наружного диаметра, максимальные касательные напряжения существенно увеличиваются. Это объясняется уменьшением момента сопротивления.

Из условия прочности при кручении, как и при растяжении и сжатии, в зависимости от постановки задачи может быть определена допускаемая нагрузка:

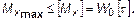
В рассмотренном примере │M_х│= 2М. Следовательно, допустимая нагрузка на вал

.

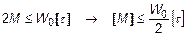Из условия прочности при кручении в зависимости от постановки задачи может быть определен диаметр вала по (25).

.

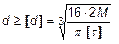3. Угловые перемещения.

Определение полного угла закручивания вала или угла поворота сечения вокруг продольной оси х производят по закону Гука при кручении (28):

.

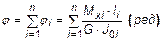Для первого участка

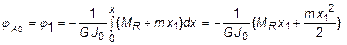, (на эпюре парабола выпуклостью вверх):

; .

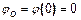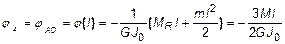Для второго участка

.

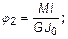
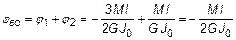Знаки перед слагаемыми соответствуют знакам внутренних крутящих моментов (рис.7,в). Физически φ₂ означает угол закручивания второго участка вала– угол поворота сечения В относительно А вокруг продоль