Кафедра «Математика и информатика»
Кафедра «Математика и информатика»
Музаев И.Д.
Теория вероятностей и математическая статистика
Методические рекомендации по выполнению контрольной работы
для студентов, обучающихся по направлению
38.03.01 Экономика (очная форма обучения)
Квалификация (степень бакалавр)
Рассмотрено и одобрено на заседании
кафедры «Математика и информатика»
протокол ___ от ______________ 2016 г.
Зав.кафедрой ____________Казарян М.Л.
Владикавказ 2016
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Необходимость освоения будущими бакалаврами менеджмента теории вероятностей и математической статистики продиктована широким использованием математических методов в современной экономической практике. Полученные математические знания делают возможным изучение прикладных и экономических наук, грамотное общение с компьютером.
Теоретический материал приведен только тот и в том объеме, который необходим для решения предлагаемых в контрольной работе задач. Каждая тема иллюстрирована большим количеством примеров, контрольная работа снабжена образцом ее выполнения.
Контрольная работа должна быть выполнена в срок (по графику учебного процесса до начала экзаменационной сессии) и оформлена в тетради в клетку. Титульный лист оформляется согласно приложению 4.
При выполнении контрольной работы студент должен придерживаться следующих требований:
- перед началом решения задачи необходимо написать полный текст условия задачи;
- решение задачи следует снабжать подробными пояснениями, расчёты по формулам должны быть приведены полностью, без сокращений;
- в задачах по математической статистике для получения правильного результата необходимо проводить промежуточные вычисления с достаточно высокой точностью (до 3 значащих цифр после запятой).
Перед решением заданий контрольной работы рекомендуется ознакомиться со всеми примерами, рассмотренными в данной работе. По каждому заданию контрольной работы в методических указаниях приводится основной теоретический материал и разбирается несколько типовых примеров.
Варианты распределить согласно таблице:
| Номер варианта | Начальная буква фамилии |
| 1. | А |
| 2. | Б |
| 3. | В |
| 4. | Г |
| 5. | Д |
| 6. | Е, Ж |
| 7. | З,И |
| 8. | К |
| 9. | Л |
| 10. | М |
| 11. | Н |
| 12. | О,Ю |
| 13. | П |
| 14. | Р |
| 15. | С |
| 16. | Т |
| 17. | У,Э |
| 18. | Ф, Я |
| 19. | Х,Щ |
| 20. | Ц,Ч |
Содержание
1 Предмет теории вероятностей и математической статистики. 5
2 Случайные события. 8
2.1. Испытания и события. 8
2.2. Виды событий. 8
2.3. Классическое определение вероятности. 10
2.4. Основные формулы комбинаторики. 11
2.5. Произведение и сумма событий. 13
2.6. Условная вероятность. вероятность произведения событий. 13
2.7. Вероятность суммы событий. 15
2.8. Формула полной вероятности. 18
2.9. Формула Байеса. 19
2.10. Последовательности испытаний. Формула Бернулли. 20
2.11. Предельные теоремы в схеме Бернулли. 22
3 Случайные величины.. 24
3.1. Понятие случайной величины.. 24
3.2. Закон распределения дискретной случайной величины.. 25
3.3. Функция распределения. 26
3.4. Вероятность попадания случайной величины на заданный интервал. 28
3.5. Плотность распределения. 29
3.6. Числовые характеристики случайной величины.. 31
3.7. Примеры дискретных распределений. 35
3.8. Примеры непрерывных распределений. 36
4 Элементы математической статистики. 41
4.1. Выборочный метод. 42
4.1.1. Генеральная совокупность и выборочная. 42
4.1.2. Вариационный ряд. полигон частот и гистограмма эмпирическая функция распределения 43
4.2. Статистическое оценивание. 47
4.2.1. Оценка параметров генеральной совокупности. точечная оценка и ее свойства 47
4.2.2. Оценка с помощью интервалов. 52
4.3. Проверка статистических гипотез. 54
4.3.1 Проверка гипотез о виде распределения. критерий согласия Пирсона. 56
5 Контрольная работа. часть 1. 60
6 Контрольная работа. часть 2. 86
6.1. Пример выполнения контрольной работы.. 95
приложение 1. 103
приложение 2. 104
приложение 3. 106
приложение 4. 107
СЛУЧАЙНЫЕ СОБЫТИЯ
Испытания и события
Случайным событием (или просто событием) называется любой факт, который может иметь место при наличии определенной совокупности условий.
Каждое осуществление требуемой совокупности условий называется испытанием или опытом.
События, которые могут произойти в результате испытания, называются исходами данного испытания. События принято обозначать заглавными (прописными) буквами начала латинского алфавита: А, В, С и т.д. Словесное описание события часто дается в такой форме:
А = {выпадение "орла" при бросании монеты}.
Виды событий
В теории вероятностей различают виды событий.
Достоверное событие. Так называют событие, которое обязательно происходит в результате испытания.
Невозможное событие – событие, которое не может произойти в данном испытании.
Совместные и несовместные события. Два события называются несовместными, если они не могут произойти вместе в одном испытании, в противном случае их называют совместными. События А1, А2, ..., Аn , называют попарно несовместными, если никакие два из них не могут произойти вместе в одном испытании.
Противоположным событию А называется событие `А, состоящее в непоявлении события А. Очевидно, что события А и `А являются несовместными.
Говорят, что события А1, А2 ,...,Аn в некотором испытании образуют полную группу, если в результате испытания обязательно должно произойти хотя бы одно из них.
Условимся полную группу несовместных исходов называть пространством элементарных событий.
Пример 2.1.Достоверным является событие А = {извлечение белого шара из урны, где все шары белые}.
Невозможным является событие B = {извлечение белого шара из урны, где все шары черные}.
Практически невозможное событие: C1={найти иголку в стоге сена}; C2=={вытащить белый шар из урны, где 1000 шаров черные, а 1 – белый}
Практически достоверное событие: D={вытащить белый шар из урны, где 999 шаров белые, а 1 – черный};
Пример 2.2.Испытание состоит в бросании игральной кости. Рассматриваем события:
А = {выпадение двух очков};
В = {выпадение трех очков};
С = {выпадение четного числа очков}.
События А и В, а также В и С являются несовместными. События А и С – совместные. Попарно несовместными события А, В, С не являются.
Пример 2.3.Производится бросание игральной кости.
А = {выпадение шести очков};
`А = {выпадение любого числа очков, кроме шести}.
Говорят, что события А1, А2 ,...,Аn в некотором испытании образуют полную группу, если в результате испытания обязательно должно произойти хотя бы одно из них.
Пример 2.4.Производится бросание монеты. Полную группу образуют события А = {выпадение "орла"}, В = {выпадение "решки"}.
Вероятность суммы событий
Теорема 2.1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Теорема 2.2. Для любого события А вероятность противоположного события А выражается равенством
Р(`А) = 1 – Р(А)
Теорема 2.3. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления:
Р(А + В) = Р(А)+ Р(В) – Р(АВ).
Теорема сложения обобщается на любое конечное число событий следующим образом:
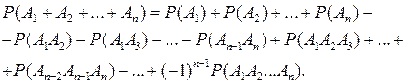 (2.3)
(2.3)
Если события А1, А2, ..., Аппопарно несовместные, то формула (2.3) принимает вид:
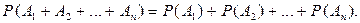
Замечание. При решении задач с использованием формулы (2.3) приходится производить громоздкие вычисления, поэтому часто выгоднее перейти к противоположным событиям, т.е. вместо вероятности суммы событий А1+А2+...+Ап находить вероятность произведения противоположного события 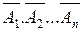 . Очевидно, что эти два события противоположны, поэтому
. Очевидно, что эти два события противоположны, поэтому
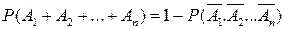 (2.4)
(2.4)
Пример 2.13. В условиях примера 2 предыдущего пункта найти вероятность появления хотя бы одной пробоины.
Решение.  Данное событие есть сумма событий А и В, причем эти события совместные, поэтому вероятность интересующего нас события равна Р(А + В) = Р(А) + Р(В) – Р(АВ). Ранее было найдено, что Р(АВ)=0.48, следовательно, Р(А + В) = 0.6 + 0.8 – 0.48 = 0.92.
Данное событие есть сумма событий А и В, причем эти события совместные, поэтому вероятность интересующего нас события равна Р(А + В) = Р(А) + Р(В) – Р(АВ). Ранее было найдено, что Р(АВ)=0.48, следовательно, Р(А + В) = 0.6 + 0.8 – 0.48 = 0.92.
Пример 2.14. Устройство содержит четыре независимо работающих элемента и сохраняет работоспособность, если работает хотя бы один из элементов. Вероятности безотказной работы элементов в течение определенного срока соответственно равны 0.9, 0.8, 0.7 и 0.6. Найти вероятность безотказной работы устройства.
Решение. Пусть события А1 А2, А3и А4означают безотказную работу соответственно первого, второго, третьего и четвертого элементов. Событие А={безотказная работа устройства} есть сумма событий: А=А1+А2+А3+А4.События А1 А2, А3и А4совместные, поэтому вероятность Р(А)надо вычислять по формуле (2.3). Чтобы упростить вычисления, воспользуемся формулой (2.4):
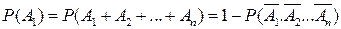 .
.
Так как события А1 А2, А3и А4независимые, то противоположные события 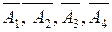 также независимы, поэтому
также независимы, поэтому
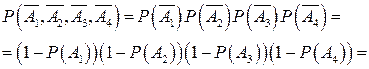
= (1 – 0.9)(1 – 0.8)(1 – 0.7)(1 – 0.6) = 0.0024; и
Р(А) = 1 – 0.0024 = 0.9976.
Пример 2.15. Производится три независимых выстрела по мишени. Вероятности попадания в мишень при первом, втором и третьем выстрелах соответственно равны 0.2, 0.5, 0.4. Найти вероятность того, что будет ровно два попадания в мишень.
Решение. Событие А={ровно два попадания в мишень} выражается через события А1={попадание при первом выстреле}, А2={попадание при втором выстреле), А3={попадание при третьем выстреле} следующим образом:
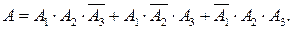
Отсюда, учитывая несовместность суммируемых произведений событий и независимость событий А1, А2, А3,находим
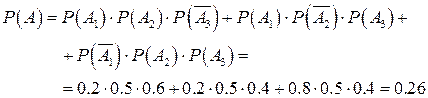
Пример 2.16. В двух урнах находятся шары, отличающиеся только цветом: в первой урне 5 белых шаров, 11 черных и 8 красных, во второй 10 белых, 8 черных и 6 красных. Из обеих урн наудачу извлекают по одному шару. Найти вероятность того, что оба шара одного цвета.
Решение. Введем в рассмотрение следующие события:
В1={извлечение белого шара из первой урны},
В2={извлечение белого шара из второй урны},
С1={извлечение черного шара из первой урны},
С2={извлечение черного шара из второй урны},
D1={извлечение красного шара из первой урны},
D2={извлечение красного шара из второй урны}.
Выразим событие А= {извлечение шаров одного цвета} через эти события:
А= В1 В2+ С1 С2+ D1 D2
Следовательно,
Р(А) = Р(В1)Р(В2) + Р(С1)Р(С2) + Р(D1)P(D2).
Вероятности событий В, С, D найдем из классического определения: Р(В1)=5/24, Р(В2)=10/24, Р(С1)=11/24, Р(С2)=8/24, Р(D1)=8/24, P(D2)=6/24.
Таким образом, получаем
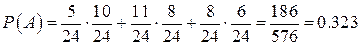
Формула полной вероятности
Пусть А – некоторое событие, которое может появиться совместно с одним из ряда попарно несовместных событий Н1, Н2,…,Нn образующих полную группу ( 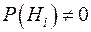 ). Будем называть события Н гипотезами.
). Будем называть события Н гипотезами.
Теорема 2.4. Вероятность события А, которое может произойти вместе с одной из гипотез Н1, Н2,…,Нn, равна сумме парных произведений вероятностей этих гипотез на соответствующие им условные вероятности события А:
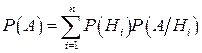
Эта формула называется формулой полной вероятности.
Пример 2.17.Первый станок производит 25%, второй – 35%, третий – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4% и 2%. Найти вероятность того, что взятое наугад изделие окажется бракованным.
Решение. Введем гипотезы:
Н1={взятое изделие изготовлено на первом станке},
Н2={взятое изделие изготовлено на втором станке},
Н3={взятое изделие изготовлено на третьем станке}.
События Н1, Н2и Н3 несовместные, образуют полную группу, и событие А ={взятое изделие – брак} происходит вместе с одним из них, следовательно, они действительно могут быть взяты в качестве гипотез для события А. Согласно формуле полной вероятности
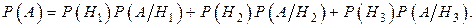
По условию задачи
Р(Н1)= 0.25, Р(Н2)=0.35, Р(Н3)=0.40, 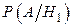 =0.05,
=0.05,
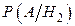 =0.04,
=0.04, 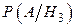 =0.02,
=0.02,
следовательно, Р(А)= 0.25 • 0.05 + 0.35 • 0.04 + 0.40 • 0.02 = 0.0345.
Замечание. Вероятности 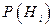 характеризуют возможность осуществления некоторых условий
характеризуют возможность осуществления некоторых условий 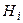 , а
, а 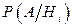 возможность появления А при этих условиях.
возможность появления А при этих условиях.
Формула Байеса
Пусть событие А может произойти совместно с одной из гипотез Н1, Н2,…, Нn . Если до проведения опыта были известны вероятности гипотез 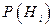 , а в результате опыта произошло событие А, то условные вероятности гипотез
, а в результате опыта произошло событие А, то условные вероятности гипотез 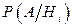 вычисляются по формуле Байеса:
вычисляются по формуле Байеса:
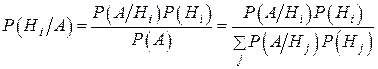
Пример 2.18.Первый станок производит 20%, а второй 80% всех деталей. Брак в их производстве составляет соответственно 4% и 2%. Взятая наугад деталь оказалась бракованной. Найти вероятность того, что эта деталь изготовлена на первом станке.
Решение. Введем две гипотезы для события А={взятая деталь оказалась бракованной}:
Н1={взятая деталь изготовлена на первом станке},
Н2={взятая деталь изготовлена на втором станке}.
Из условия задачи известно: Р(Н1)= 0.2, Р(Н2)=0.8, 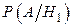 =0.04,
=0.04, 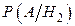 =0.02.. По формуле Байеса находим
=0.02.. По формуле Байеса находим
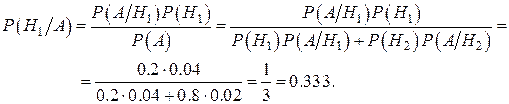
Замечание. Формула Байеса указывает путь использования новых экспериментальных данных для коррекции априорных (доопытных) вероятностных представлений об исследуемом объекте.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Понятие случайной величины
Случайной величиной называется величина, которая в результате испытаний, проводимых в одних и тех же условиях, принимает различные, вообще говоря, значения, зависящие от не учитываемых случайных факторов. Примеры случайных величин: число выпавших очков на игральной кости, число дефектных изделий в партии, отклонение точки падения снаряда от цели, время безотказной работы устройства и т.п. Различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, возможные значения которой образуют счетное множество, конечное или бесконечное (т.е. такое множество, элементы которого могут быть занумерованы).
Непрерывной называется случайная величина, возможные значения которой непрерывным образом заполняют некоторый конечный или бесконечный интервал числовой оси. Число значений непрерывной случайной величины всегда бесконечно.
Случайные величины будем обозначать заглавными буквами конца латинского алфавита: X, Y, ...; значения случайной величины – строчными буквами: х, у, ... . Таким образом, X обозначает всю совокупность возможных значений случайной величины, а х – некоторое ее конкретное значение.
Функция распределения
Функция распределения является универсальной формой задания закона распределения как дискретных, так и непрерывных случайных величин.
Функцией распределения случайной величины X называется функция F(x), определенная на всей числовой оси следующим образом:
F(x)= Р(Х < х),
т.е. F(x) есть вероятность того, что случайная величина X примет значение меньшее, чем x.
Функцию распределения можно представить графически. Для дискретной случайной величины график имеет ступенчатый вид. Построим, например, график функции распределения случайной величины, заданной следующим рядом (рис. 3.1):
| X | |||
| p | 0.3 | 0.5 | 0.2 |
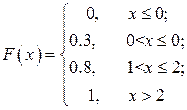 | 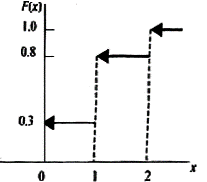 |
Рис. 3.1. График функции распределения дискретной случайной величины
Скачки функции происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. В точках разрыва функция F(x)непрерывна слева.
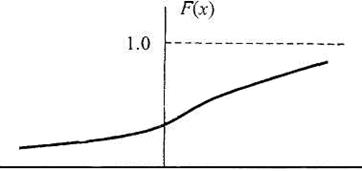
График функции распределения непрерывной случайной величины представляет собой непрерывную кривую.
 x x |
Рис. 3.2. График функции распределения непрерывной случайной величины
Функция распределения обладает следующими очевидными свойствами:
1) 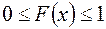 , 2)
, 2) 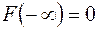 , 3)
, 3) 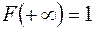 ,
,
4) 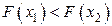 при
при 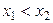 .
.
Плотность распределения
Для непрерывных случайных величин наряду с функцией распределения используется еще одна форма задания закона распределения – плотность распределения.
Если 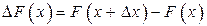 – вероятность попадания на интервал
– вероятность попадания на интервал 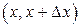 , то отношение
, то отношение 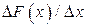 характеризует плотность, с которой вероятность распределена в окрестности точки x . Предел этого отношения при
характеризует плотность, с которой вероятность распределена в окрестности точки x . Предел этого отношения при 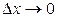 ,т.е. производная
,т.е. производная 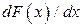 , называется плотностью распределения (плотностью распределения вероятностей, плотностью вероятности) случайной величины X. Условимся плотность распределения обозначить
, называется плотностью распределения (плотностью распределения вероятностей, плотностью вероятности) случайной величины X. Условимся плотность распределения обозначить
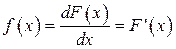 .
.
Таким образом, плотность распределения характеризует вероятность попадания случайной величины в окрестность точки х.
График плотности распределения называют кривой распределения (Рис. 3.4).
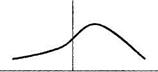
Рис. 3.4. Вид плотности распределения
Исходя из определения и свойств функции распределения F(x),нетрудно установить следующие свойства плотности распределения f(x):
1) f(x)³0
2) 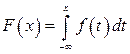
3) 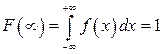
4) 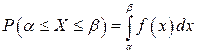
Для непрерывной случайной величины в силу того, что вероятность попадания в точку равна нулю, имеют место следующие равенства: 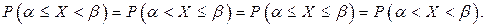
Пример 3.2. Случайная величина X задана плотностью распределения
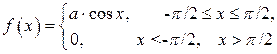
Требуется:
а) найти значение коэффициента а;
б) найти функцию распределения;
в) найти вероятность попадания случайной величины на интервал (0, 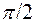 ).
).
Решение, а) Воспользуемся свойством 3:
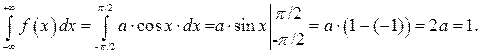
Отсюда получаем: а=1/2.
б) Если 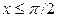 , то
, то
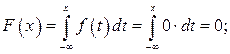
если 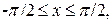 то
то
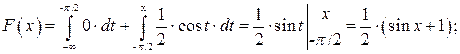
если 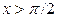 , то
, то
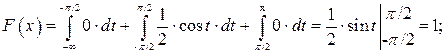
Таким образом,
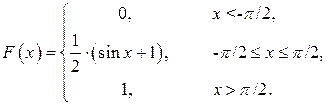
в) По свойству 4:
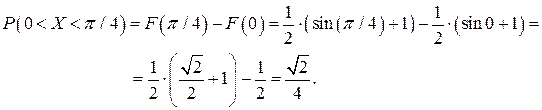
Примеры дискретных распределений
1. Биномиальное распределение. Случайная величина 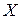 , равная числу «УСПЕХОВ» в схеме Бернулли, имеет биномиальное распределение:
, равная числу «УСПЕХОВ» в схеме Бернулли, имеет биномиальное распределение: 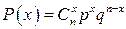 ,
, 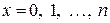 .
.
Математическое ожидание случайной величины, распределённой по биноминальному закону, равно
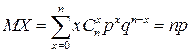 .
.
Дисперсия этого распределения равна 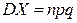 .
.
2. Распределение Пуассона 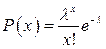 ,
, 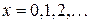
Математическое ожидание и дисперсия случайной величины с распределением Пуассона 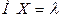 ,
, 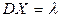 .
.
Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства, например: число машин, прибывших на автомойку в течении часа, число остановок станков в неделю, число дорожных происшествий и т.д.
3. Геометрическое распределение
Случайная величина 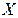 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 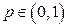 , если
, если 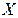 принимает значения
принимает значения 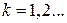 с вероятностями
с вероятностями 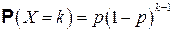 . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха
. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха 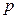 . Таблица распределения
. Таблица распределения 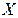 имеет вид:
имеет вид:
 |
Примеры непрерывных распределений
1. Равномерное распределение. Плотность равномерного или прямоугольного распределения:
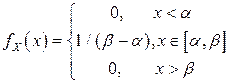 ,
,
т.е. вероятности 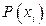 всех возможных значений
всех возможных значений 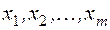 случайной величины
случайной величины 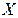 одинаковы и равны
одинаковы и равны 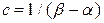 .
.
Математическое ожидание случайной величины с равномерным распределением равно
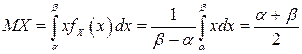 ,
,
дисперсия 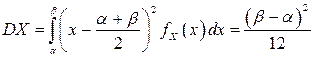 .
.
Функция распределения имеет вид 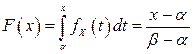 ,
, 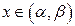 (рис. 3.5).
(рис. 3.5).
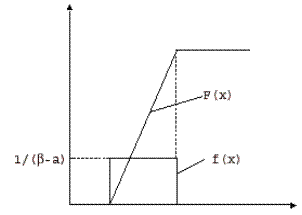
Рис. 3.5. Графики плотности и функции равномерного распределения
2. Показательное (экспоненциальное) распределение -закон, функция плотности распределения которого имеет вид: 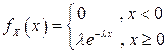 , где параметр распределения
, где параметр распределения 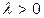 есть действительное число (постоянный параметр) (рис. 3.6).
есть действительное число (постоянный параметр) (рис. 3.6).
Функция распределения показательного закона имеет вид:
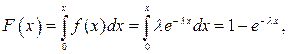
Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону, равны соответственно 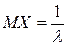 ,
, 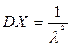 .
.
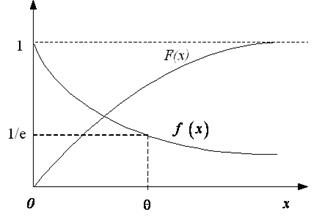
Рис. 3.6. Графики плотности и функции показательного распределения
3. Нормальное распределение.Нормальный закон распределения вероятностей занимает особое место среди других законов распределения. В теории вероятности доказывается, что плотность вероятности суммы независимых или слабо зависимых, равномерно малых (т.е. играющих примерно одинаковую роль) слагаемых при неограниченном увеличении их числа как угодно близко приближается к нормальному закону распределению независимо от того, какие законы распределения имеют эти слагаемые (центральная предельная теорема А. М. Ляпунова).
Плотность вероятности нормально распределенной случайной величины 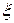 имеет вид:
имеет вид: 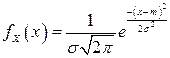 , где
, где 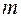 и
и 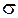 – вещественные параметры распределения, имеющие конечные значения, при этом часто используют обозначение
– вещественные параметры распределения, имеющие конечные значения, при этом часто используют обозначение  .
.
Функция распределения записывается в виде
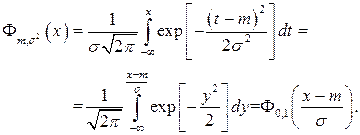 ,
,
Здесь 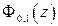 – табулированный интеграл вероятности (значения интеграла можно найти во всех учебниках и задачниках по теории вероятностей). Функция и плотность нормального распределения изображены на рис. 3.7.
– табулированный интеграл вероятности (значения интеграла можно найти во всех учебниках и задачниках по теории вероятностей). Функция и плотность нормального распределения изображены на рис. 3.7.
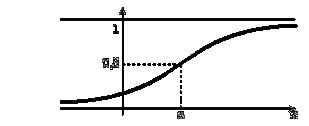
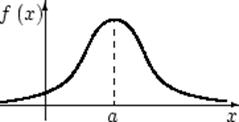
Рис. 3.7. Графики плотности и функции нормального распределения
Математическое ожидание нормально распределенной случайной величины равно 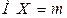 , дисперсия
, дисперсия 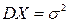 . Таким образом, параметры
. Таким образом, параметры 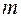 и
и 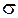 имеют смысл математического ожидания и среднеквадратического значения (отклонения) случайной величины.
имеют смысл математического ожидания и среднеквадратического значения (отклонения) случайной величины.
Распределение, описываемое функцией 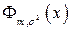 , называется нормальным или распределением Гаусса.
, называется нормальным или распределением Гаусса.
На рис.3.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения 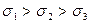 .
.
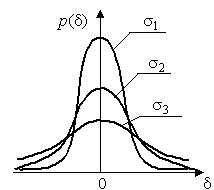
Рис. 3.8. Кривые нормального распределения, 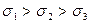 .
.
Из рис. 3.8 видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.
Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики – Муавр, Лаплас, Гаусс, Чебышев и Ляпунов.
Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
Свойства нормального распределения.
А. Если случайная величина 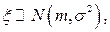
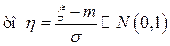 .
.
В. Если случайная величина 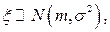 то
то
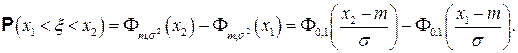
В частности, 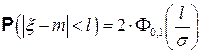 .
.
Таким образом, вычисление любых вероятностей для нормально распределённой случайной величины сводится к вычислению функции распределения 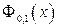 . Она обладает следующими свойствами:
. Она обладает следующими свойствами: 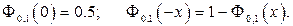
С. Если 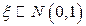 , то для любого
, то для любого 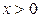
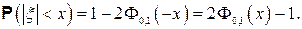
D.Правило трех сигм. Если 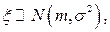 то
то
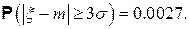
Большого смысла в запоминании числа 0.0027 нет, но полезно помнить, что почти вся масса нормального распределения сосредоточена в границах от 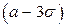 до
до 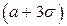 .
.
Пример 3.7. Дана случайная величина 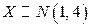 . Найти
. Найти 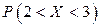 .
.
Решение. По формуле свойства В при 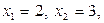
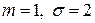 получаем
получаем 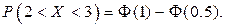 По таблице для функции Лапласа находим
По таблице для функции Лапласа находим 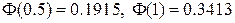 .
.
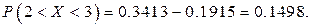
Пример 3.8.Случайная величина X – отклонение размера изделия от нормы – нормально распределенная, причём М (Х)= 0. Найти s (Х), если известно, что Р(– 3 < X < 3) = 0.7.
Решение. Р(– 3 < X < 3) = Р( | X |< 3) = 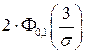 = 0.7. Отсюда следует, что
= 0.7. Отсюда следует, что 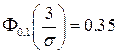 , и, используя табличные данные (приложение 1), получаем 3/s =1.4, или s = 3/1.4 » 2.14.
, и, используя табличные данные (приложение 1), получаем 3/s =1.4, или s = 3/1.4 » 2.14.
Выборочный метод
Пример 4.1.
1. Измерена масса тела 10-ти детей 6-ти лет. Полученные данные образуют простой статистический ряд: 24 22 23 28 24 23 25 27 25 25.
2. Из 10000 выпущенных на конвейере электрических лампочек отобрано 300 штук для проверки качества всей партии. Здесь 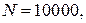 а
а 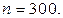
Отдельные значения статистического ряда называются вариантами. Если варианта хi появилась m раз, то число m называют частотой, а ее отношение к объему выборки m/n – относительной частотой.
Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется ранжированным рядом.
Пример 4.2. Для ранжированного ряда: 23 23 24 24 25 25 25 27 28 в нижеприведенной таблице в первой строке записаны все значения величины (варианты), во второй – соответствующие им частоты (безынтервальный вариационный ряд), в третьей – накопленные частоты, в четвертой – относительные частоты (табл.4.1).
Таблица 4.1. Значения вариант и их частот
| Х | ||||||
| ni | ||||||
| nн | ||||||
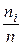 | 0.1 | 0.2 | 0.2 | 0.3 | 0.1 | 0.1 |
Полигоном частот называют ломаную линию, отрезки которой соединяют точки с координатами (хi; ni) (рис. 4.1).
Отметим, что сумма частот статистического ряда равна объему выборки. Часто статистический ряд составляют, используя относительные частоты вариант: 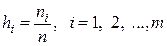 (m — количество различных вариант). Сумма относительных частот равна единице.
(m — количество различных вариант). Сумма относительных частот равна единице.
Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки с координатами (хi; hi).
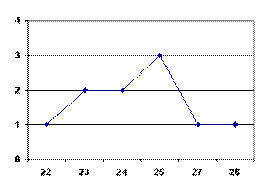 | 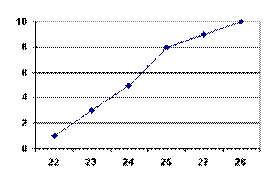 |
| а) | б) |
Рисунок 4.1. Полигон частот а), кумулятивная кривая б)
Эмпирическим аналогом графика интегральной функции распределения является кумулятивная кривая (кумулята). Для ее построения на оси ОХ откладывают значения вариант, на оси ОY – накопленные частоты или относительные частоты. Полученная плавная кривая называется кумулятой.
В том случае, если выборка представлена большим количеством различных значений непрерывной случайной величины, то группировку данных проводят в виде интервального вариационного ряда (ИВР). Для этого диапазон варьирования признака разбивают на несколько (5–10) равных интервалов и указывают количество вариант, попавших в каждый интервал.
Алгоритм построения интервального вариационного ряда.
1. Исходя из объема выборки (n), определить количество интервалов (k) (см. табл. 4.2).
Таблица 4.2.Рекомендуемое соотношениеобъем выборки-число интервалов
| n | 25–40 | 40–60 | 60–100 | 100–200 | >200 |
| k | 5–6 | 6–8 | 7–10 | 8–12 | 10–15 |
2. Вычислить размах ряда: R=Xmax – Xmin
3. Определить ширину интервала: h=R/(k–1)
4. Найти начало первого интервала X0 = Xmin – h/2
5. Составить интервальный вариационный ряд.
Графическим изображением ИВР является гистограмма. Для ее построения на оси ОХ откладывают интервалы шириной h, на каждом интервале строят прямоугольник высотой m/h. Величина m/h называется плотностью частоты. Гистограмма является эмпирическим аналогом графика дифференциальной функции распределения.
Пример 4.3. Измерена масса тела 100 женщин 30 лет, получены значения от 60 до 90 кг. Построить интервальный вариационный ряд (табл. 4.3) и гистограмму.
Таблица 4.3. Интервальный вариационный ряд
| Интервал | Середина интервала | m | m/h |
| 60–65 | 62.5 | 2.8 | |
| 65–70 | 67.5 | 6.4 | |
| 70–75 | 72.5 | 5.6 | |
| 75–80 | 77.5 | 2.8 | |
| 80–85 | 82.5 | 1.4 | |
| 85–90 | 87.5 Наши рекомендации
|
