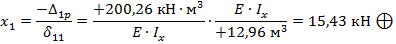Раскрытие статической неопределимости

0) Определим степень статической неопределимости рамы:

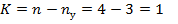à cистема один раз статически неопределима

а) Создадим основную систему; она представлена на рисунке 2:

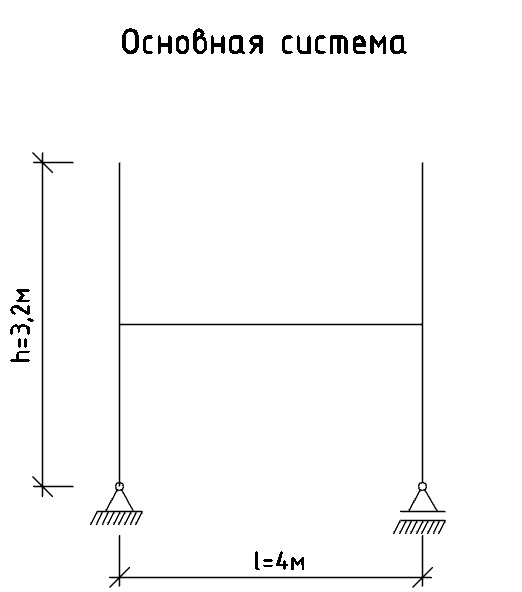
Рис. 2 - Основная система рамы

б) Создадим эквивалентную систему; представлена на рисунке 3:

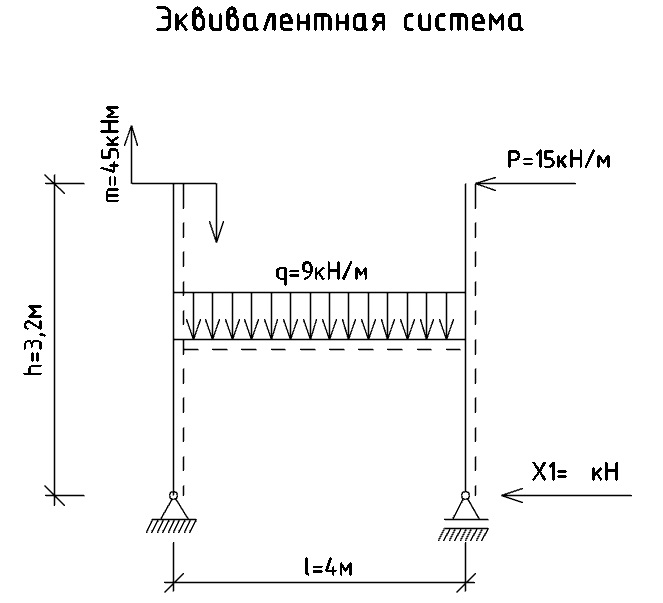
Рис. 3 - Эквивалентная система рамы

1.1 Определение опорных реакции от внешней нагрузки

а)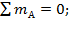

= =

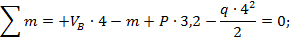
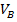
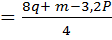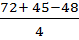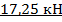
б)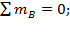

= = =

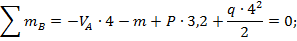
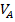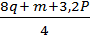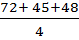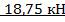
в) Проверка 1:

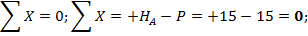
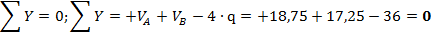
г) Проверка 2:

;

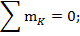
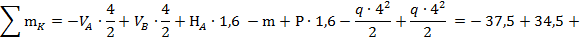
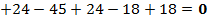На рисунке 4 представлена эквивалентная система с обозначенными на ней реакциями опор:

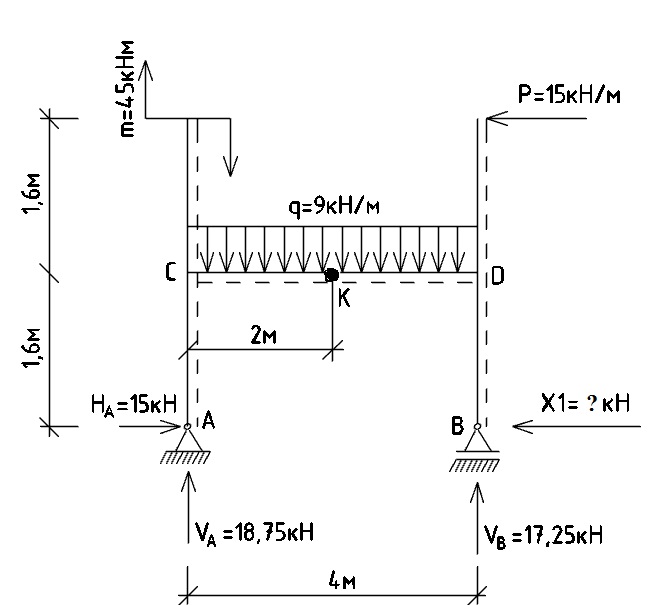
Рис. 4 - Эквивалентная система рамы с опорными реакциями

Построение эпюры Q

Результат построения эпюры перерезывающей силы представлен на рисунке 5:

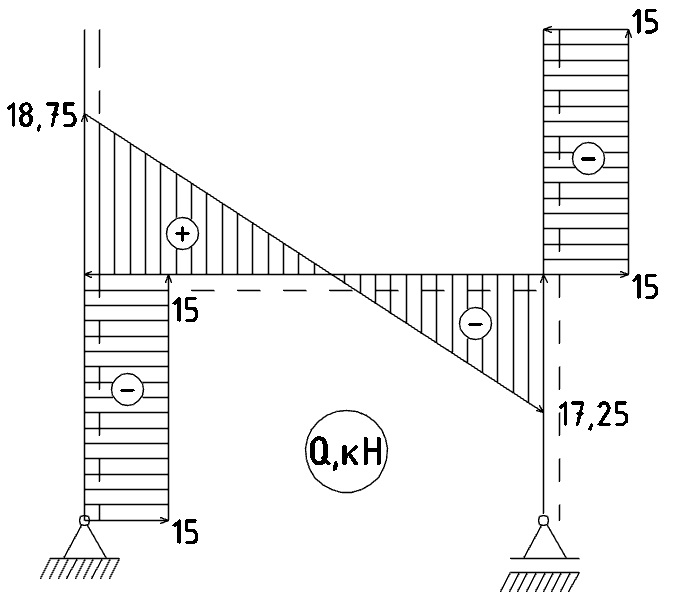
Рис. 5 - Эпюра перерезывающей силы Q

Построение эпюры М

Результат построения эпюры изгибающих моментов от внешних нагрузок представлен на рисунке 6:

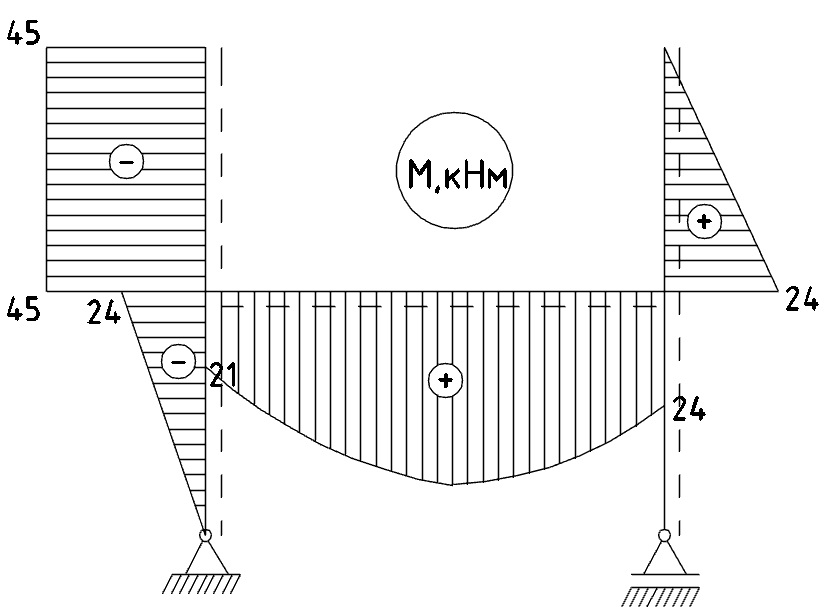
Рис. 6 - Эпюра изгибающих моментов М

1.4 Проверка правильности построения эпюры М с помощью метода вырезания узлов:

а) Узел С: вырезанный узел представлен на рисунке 7:

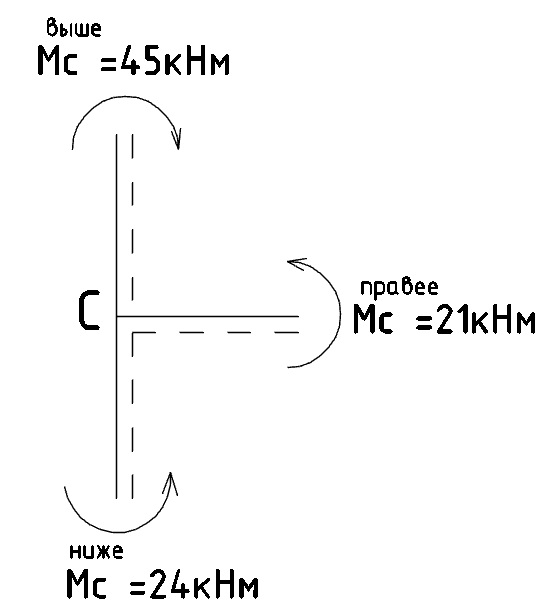
Рис. 7 - Вырезанный узел С

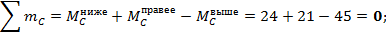
б) Узел D: вырезанный узел представлен на рисунке 8:

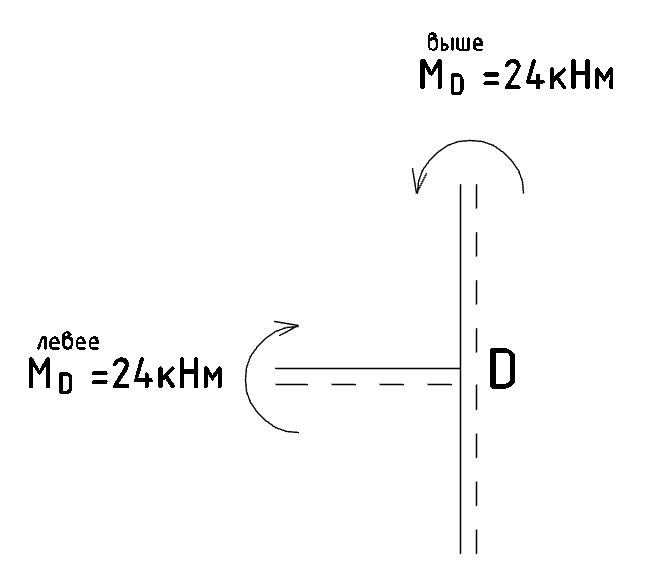
Рис. 8 - Вырезанный узел D

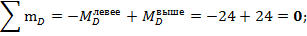
Вывод: эпюры изгибающих моментов построены правильно

1.5 Составление рамы, нагруженной единичной силой X₁

Схема представлена на рисунке 9:

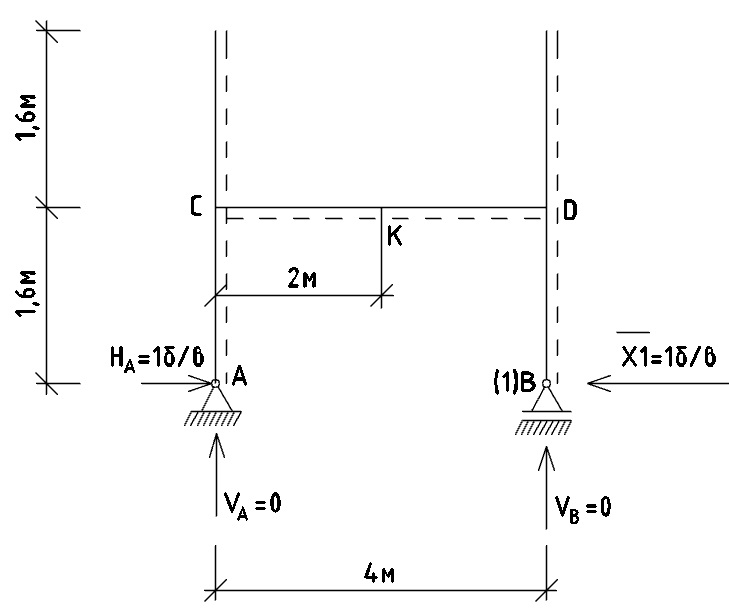
Рис. 9 - Рама, нагруженная единичной силой в точке 1(В)

а) Определение опорных реакции:

; ;

; ;

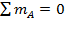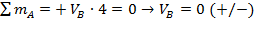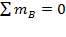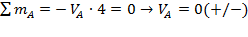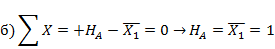
в) Проверка: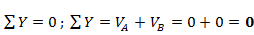

г) Проверка: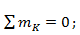

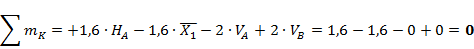
Построение эпюры Q

На рисунке 10 представлена эпюра перерезывающей силы Q:

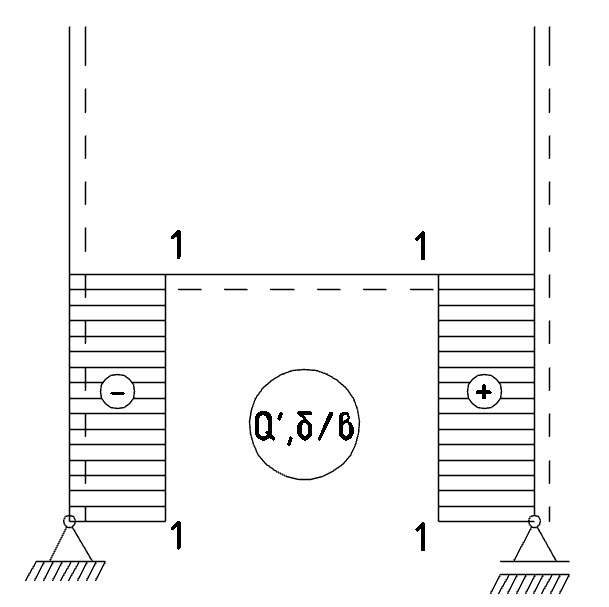
Рис. 10 - Эпюра перерезывающей силы Q’

1.5.2 Построение эпюры M

На рисунке 11 представлена эпюра изгибающих единичных моментов Мi:

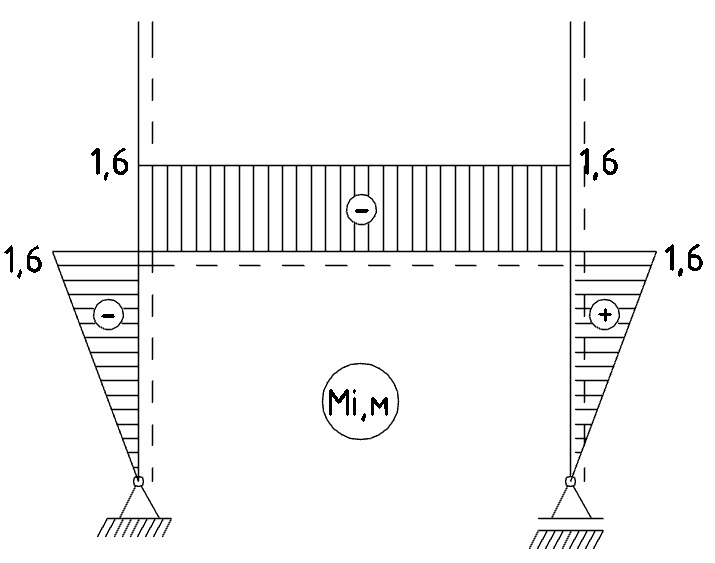
Рис. 11- Эпюра изгибающих единичных моментов Mi

1.5.3 Проверка равновесия узлов:

а) Узел C: на рисунке 12 изображён вырезанный узел С:

Рис. 12 - Вырезанный узел С

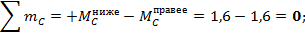
б) Узел D: на рисунке 13 изображён вырезанный узел D:

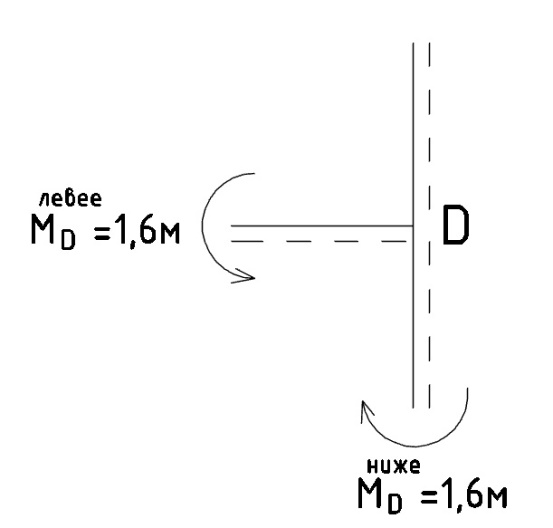
Рис. 13 - Вырезанный узел D

Определение перемещения т.1 от внешней нагрузки по методу Мора-Верещагина

а) Производится разбиение грузовой эпюры на простые геометрические фигуры – результат представлен на рисунке 14:

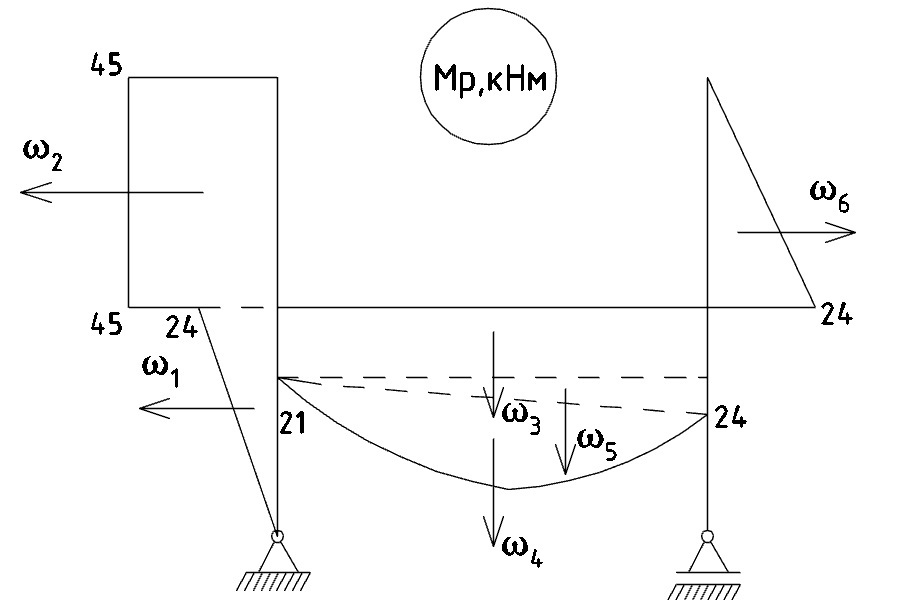
Рис. 14 - Разбиение грузовой эпюры на простые геометрические фигуры;

б) Определяются площади простых фигур :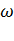

;

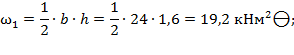
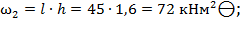
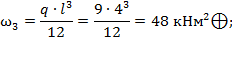
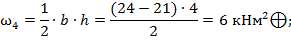
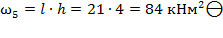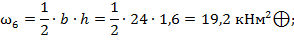
в) Определяются значения единичных моментов y (эпюра единичных моментов представлена на рисунке 15):

;

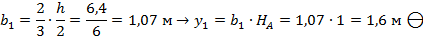
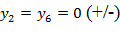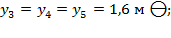
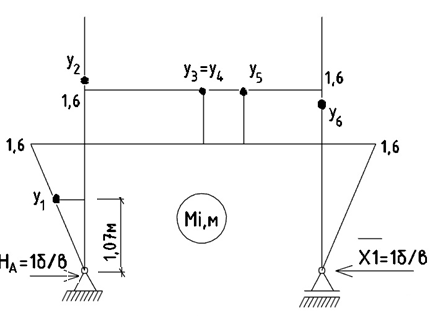
Рис. 15 – Эпюра единичных моментов y;

г) Определим перемещение точки 1(В) от внешней нагрузки:

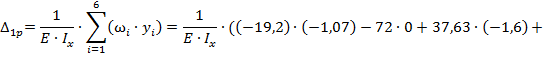
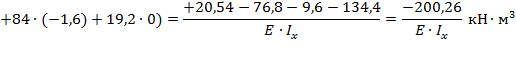
Определение перемещения т.1 от единичной силы по методу Мора-Верещагина

а) Построение грузовой эпюры от единичной силы 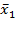: эпюра представлена на рис.16:

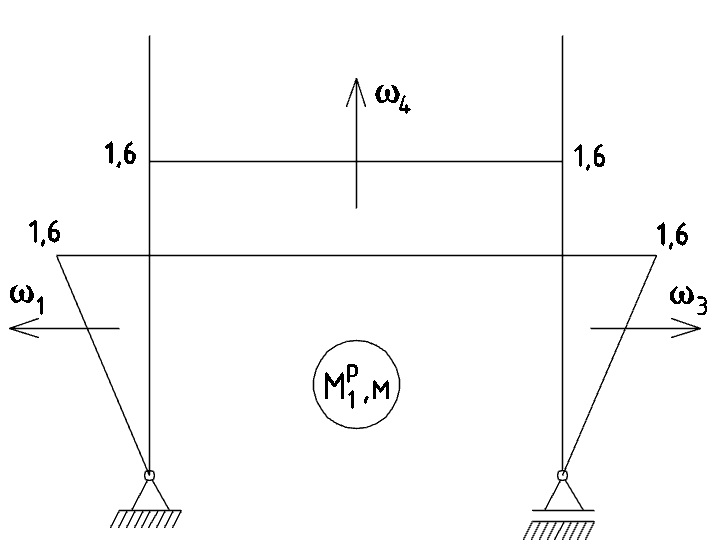
Рис. 16 - Грузовая эпюра моментов от единичной силы X₁

Определяются площади простых фигур :

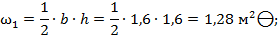
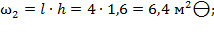
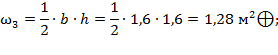
б) Построение эпюры единичных моментов от единичной силы 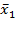: эпюра представлена на рисунке 17:

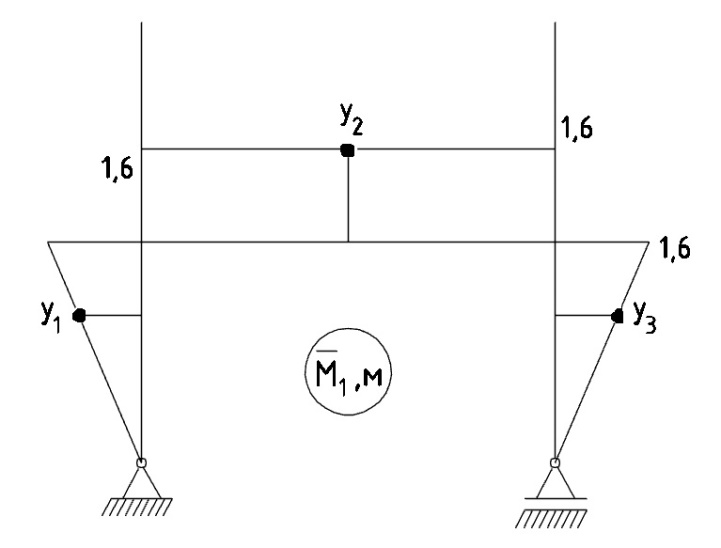
Рис. 17 - Эпюра единичных моментов от единичной силы x₁

Определяются значения единичных моментов y:

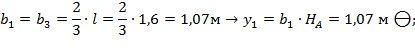
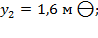
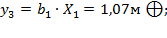
в) Определяется перемещение точки 1(В) от внешней нагрузки:

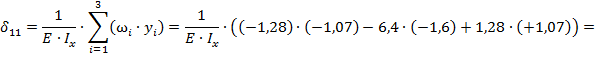
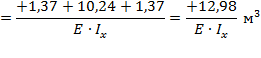
1.8 Определение неизвестной силы X₁