Ассоциированный закон пластического течения
Все теории пластичности основаны на том, что в девиаторном пространстве существует область упругой работы, ограниченная некоторой поверхностью (рис.5.1). Если девиатор напряжений 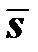 в девиаторном пространстве лежит внутри области упругой работы, то его малое приращение
в девиаторном пространстве лежит внутри области упругой работы, то его малое приращение 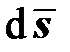 влечет за собой лишь изменение девиатора упругой деформации
влечет за собой лишь изменение девиатора упругой деформации 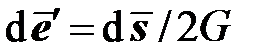 , пластическая составляющая при этом остается неизменной. Граница области упругой работы материала зависит от предела текучести материала при одноосном растяжении
, пластическая составляющая при этом остается неизменной. Граница области упругой работы материала зависит от предела текучести материала при одноосном растяжении
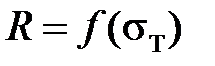
называется поверхностью текучести. Поверхность текучести определяется обычно либо критерием Губера-Мизеса, либо – Треска-Сен-Венана.
 |
| Рис.5.1 |
Изотропия девиаторного пространства требует, чтобы поверхность текучести была сферой (критерий Губера-Мизеса), радиус которой равен
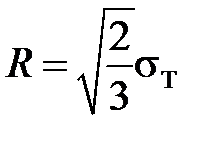 ,
,
поскольку эта величина представляет максимальную интенсивность напряжений при одноосном растяжении в области упругой работы. В расчетах вместо требования изотропии девиаторного пространства, приводящего к поверхности текучести Мизеса, иногда используют критерий текучести Треска-Сен-Венана. В трехмерном подпространстве L3 = {h1, h2, h3} девиаторного пространства такая поверхность текучести представляет фигуру вращения правильного шестиугольника вокруг оси h1. В подпространстве {h4, h5, h6}, то есть при чистом сдвиге, поверхность Треска-Сен-Венана представляет сферу, радиус которой меньше, чем в критерии Мизеса 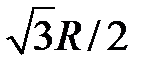 .
.
Постулат устойчивости Друкера применительно к пластическому материалу ведет к весьма важным следствиям. Продолжая рассматривать в качестве объекта исследования элементарный объем среды, в качестве нагрузки рассмотрим тензор напряжений. Элементарная работа напряжений dA на соответствующих деформациях представляет произведение
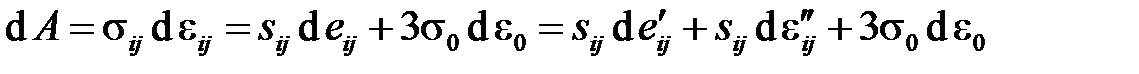 .
.
Последнее слагаемое 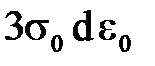 здесь представляет полный дифференциал ввиду линейной зависимости между средним напряжением s0 и деформацией e0. Для устойчивости достаточно, чтобы коэффициент этой связи 3K0 (объемный модуль упругости) был положителен, что наблюдается всегда, так что с этой стороны устойчивости ничего не грозит. Ввиду линейной связи между девиатором напряжений
здесь представляет полный дифференциал ввиду линейной зависимости между средним напряжением s0 и деформацией e0. Для устойчивости достаточно, чтобы коэффициент этой связи 3K0 (объемный модуль упругости) был положителен, что наблюдается всегда, так что с этой стороны устойчивости ничего не грозит. Ввиду линейной связи между девиатором напряжений 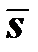 и девиатором упругих деформаций
и девиатором упругих деформаций 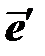 слагаемое (
слагаемое ( 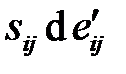 ) также представляет собой полный дифференциал, то есть при нагружении и последующем снятии нагрузки работа напряжений на упругих деформациях возвращается к нулю. Слагаемое (
) также представляет собой полный дифференциал, то есть при нагружении и последующем снятии нагрузки работа напряжений на упругих деформациях возвращается к нулю. Слагаемое ( 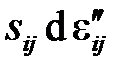 ) в этом выражении определяет рассеяние энергии в тепло, которое в изотермическом процессе удаляется системой поддержания постоянной температуры.
) в этом выражении определяет рассеяние энергии в тепло, которое в изотермическом процессе удаляется системой поддержания постоянной температуры.
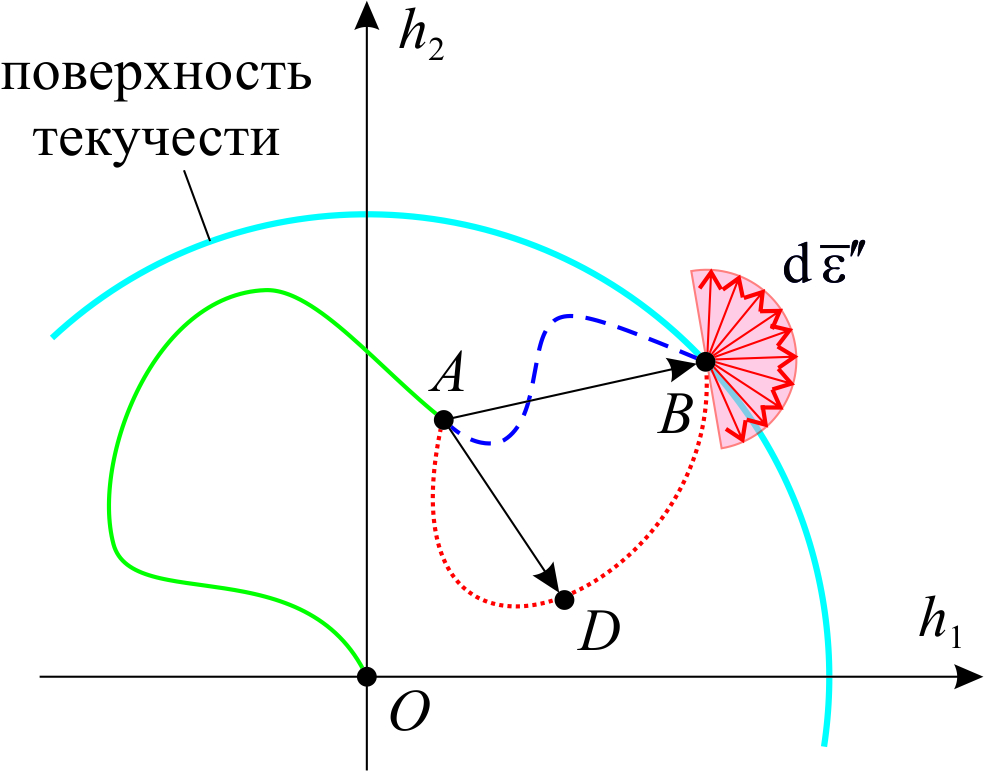
Рассмотрим цикл нагружения и снятия нагрузки из некоторого нагруженного начального состояния A (рис.4.6а). Здесь показаны часть девиаторного пространства, захватывающая область упругого деформирования (в окрестности точки O), ограниченная поверхностью текучести, и закритическая часть девиаторного пространства. После нагружения OA (сплошная линия) было произведено дополнительное нагружение (пунктирная линия) до точки B, лежащей на поверхности текучести и затем дополнительная нагрузка снята (штриховая линия), осталась только начальная (точка A). В соответствии с постулатом устойчивости работа дополнительных напряжений на пунктирной линии AB положительна. Поскольку пока нет неупругих деформаций, приращение напряжений и соответствующее приращение деформаций определяются законом Гука, то есть в девиаторном пространстве эти два приращения отличаются в 2G раз и, естественно, коллинеарны. Для примера показано некоторое промежуточное состояние (точка D). Вектор AD представляет изменение девиатора деформаций с момента выхода из точки A и одновременно соответствующее изменение девиатора напряжений, деленое на 2G. Совершенная работа этих напряжений равна к текущему моменту квадрату длины вектора AD, деленному на 4G.
 |  |
| а) | б) |
| Рис.5.2 |
При снятии дополнительной нагрузки (штриховая линия ВA) работа дополнительного напряжения отрицательна и, поскольку не было выхода за область упругой работы, за цикл нагружение – разгрузка суммарная работа напряжений равной нулю. Однако в состоянии B (в отличие от состояний в области упругой работы) допускается некоторое изменение пластической деформации 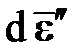 . Вспомним второе положение постулата устойчивости Друкера, которое касается неотрицательности работы дополнительных нагрузок. Из него следует, что угол между вектором AB (соответствующим приращению девиатора напряжения) и вектором
. Вспомним второе положение постулата устойчивости Друкера, которое касается неотрицательности работы дополнительных нагрузок. Из него следует, что угол между вектором AB (соответствующим приращению девиатора напряжения) и вектором 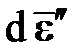 должен быть меньше π/2, чтобы его косинус, необходимый для вычисления работы, был неотрицателен. Если вдобавок вспомнить, что точка A может находиться в любом месте области упругой работы материала, включая поверхность текучести (рис.5.2б), то множество возможных направлений вектора
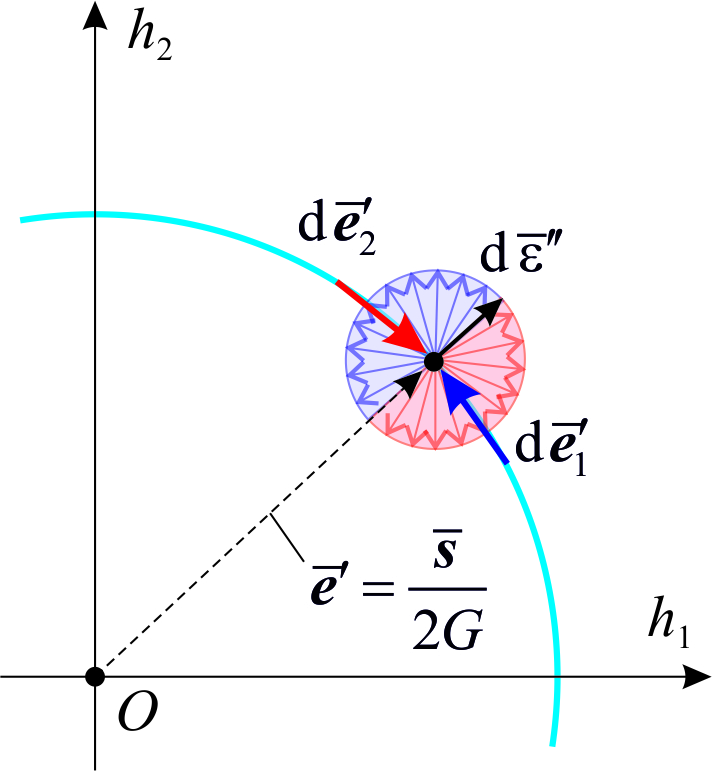
должен быть меньше π/2, чтобы его косинус, необходимый для вычисления работы, был неотрицателен. Если вдобавок вспомнить, что точка A может находиться в любом месте области упругой работы материала, включая поверхность текучести (рис.5.2б), то множество возможных направлений вектора 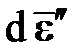 вырождается до единственного – по наружной нормали к поверхности текучести. В этом и состоит ассоциированный закон пластического течения, согласно которому вектор пластической деформации
вырождается до единственного – по наружной нормали к поверхности текучести. В этом и состоит ассоциированный закон пластического течения, согласно которому вектор пластической деформации 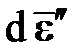 в девиаторном пространстве направлен по нормали к поверхности текучести. Отсюда следует, что при использовании шаровой поверхности текучести Губера-Мизеса векторы приращений упругой и пластической деформации взаимоортогональны, а векторы
в девиаторном пространстве направлен по нормали к поверхности текучести. Отсюда следует, что при использовании шаровой поверхности текучести Губера-Мизеса векторы приращений упругой и пластической деформации взаимоортогональны, а векторы 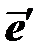 и
и 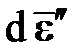 (а также
(а также 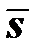 и
и 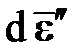 ) сонаправлены друг с другом:
) сонаправлены друг с другом:
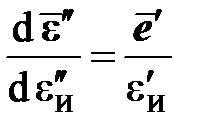 ,
, 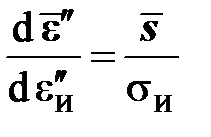 .
.
 |
| Рис.5.3 |
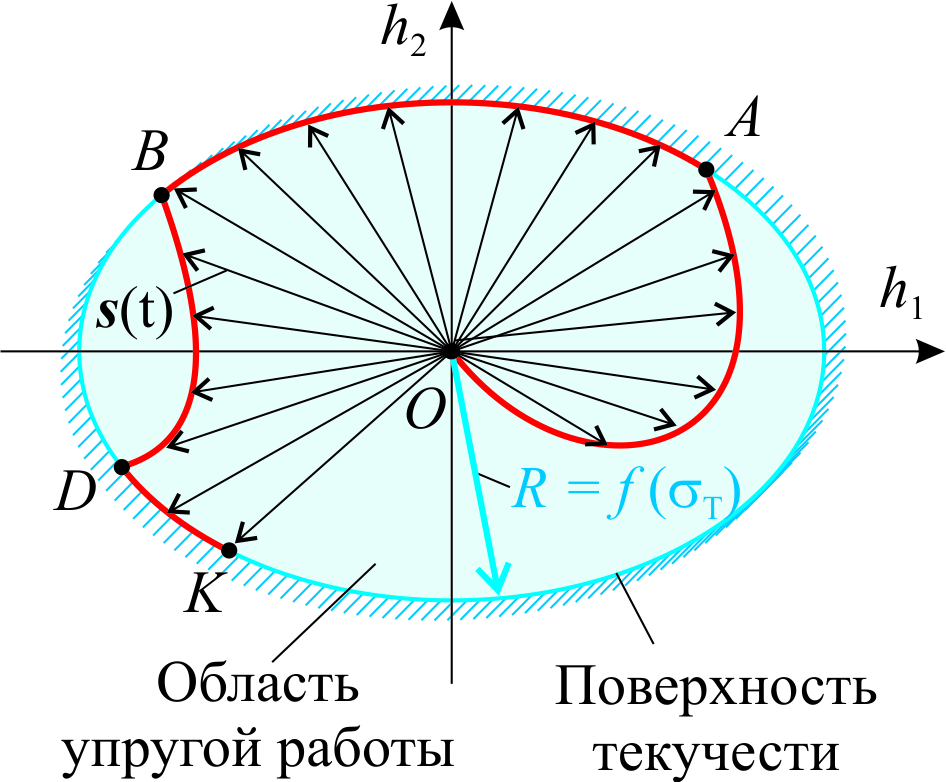
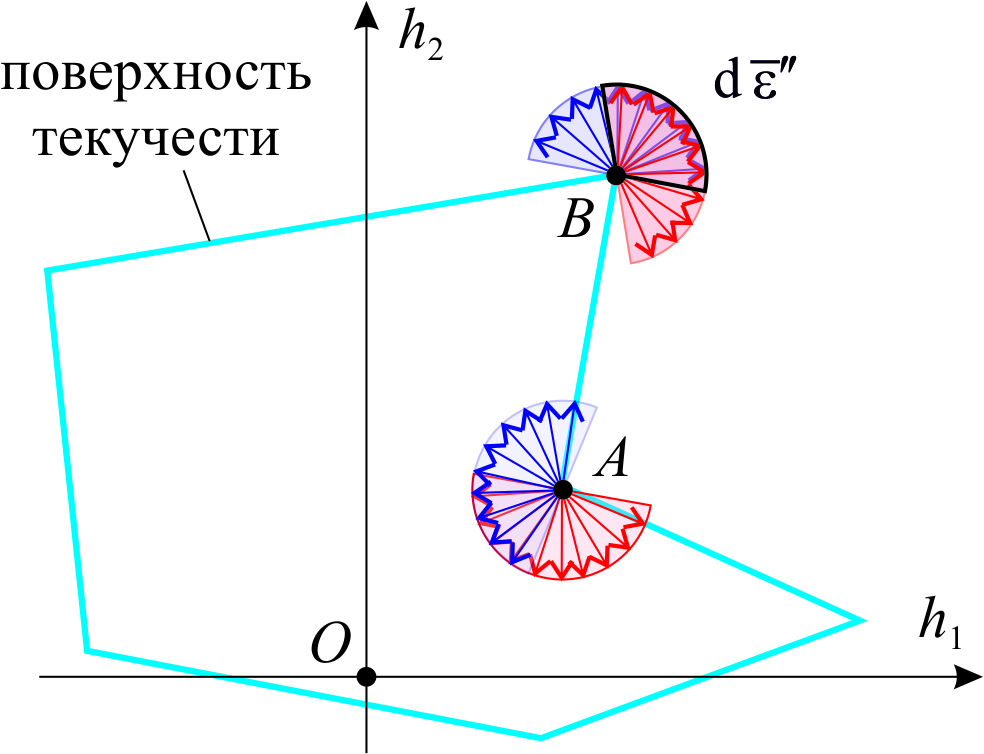
В заключении добавим, что постулат Друкера не запрещает негладкую поверхность текучести. Из него следует ее обязательная невогнутость (при этом не имеет значения, является ли поверхность текучести гладкой или нет), а также множественность возможных направлений вектора 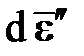 в сингулярных (угловых) точках. На рис. 5.3 показано, что в точке A, где поверхность текучести вогнута, вектор приращения пластической деформации A не существует. Точка B является сингулярной на выпуклом участке поверхности текучести, здесь приращение пластической деформации существует и может быть реализовано множеством вариантов, которое показано здесь черной сплошной линией.
в сингулярных (угловых) точках. На рис. 5.3 показано, что в точке A, где поверхность текучести вогнута, вектор приращения пластической деформации A не существует. Точка B является сингулярной на выпуклом участке поверхности текучести, здесь приращение пластической деформации существует и может быть реализовано множеством вариантов, которое показано здесь черной сплошной линией.
