Предел функции в точке. Предел функции на бесконечности.
Предел функции и его свойства.
Бесконечно малые функции, их свойства. Связь с бесконечно большими.
Бесконечно большие функции. Связь с бесконечно малыми.
Теорема о связи функции, ее предела и бесконечно малой функции.
8. Неопределенности. Способы раскрытия неопределенностей [0/0].
9. неопределенности. Способы раскрытия неопределенностей [беск./беск.]
Эквивалентные бесконечно малые и их использование при вычислении пределов.
Теоремы об эквивалентных бесконечно малых функциях.
Первый и второй замечательные пределы.
13. Таблица эквивалентных бесконечно малых функций. Вывод соотношений 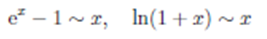
14. Таблица эквивалентных бесконечно малых функций. Вывод соотношений 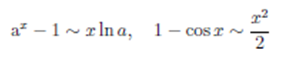
15. Сравнение бесконечно малых. Таблица эквивалентных бесконечно малых (без вывода).
Непрерывность функции. Точки разрыва функции и их классификация.
Свойства функции, непрерывных на отрезке (теоремы Вейерштрасса и Больцано-Коши)
18. Производная функции одной переменной. Основные определения. Геометрический и механический смысл.
Связь между дифференцируемостью и непрерывностью.
Дифференциал функции одной переменной. Необходимое и достаточное условие существования дифференциала. Геометрический смысл.
Дифференциал. Геометрический смысл. Применение Дифференциала к приближенным вычислениям.
22.Дифференциал. Инвариантность формы дифференциала первого порядка.
Основные правила дифференцирования. Производная постоянной, производная суммы.
Основные правила дифференцирования. Производная произведения.
Производные сложной и обратной функции.
Формулы дифференцирования. Производная логарифмической функции.
Формулы дифференцирования. Производная показательной функции.
Формулы дифференцирования. Производные тригонометрических функций.
Формулы дифференцирования. Формулы обратных тригонометрических функций.
Логарифмическое дифференцирование. Производная показательно степенной функции.
Основные теоремы дифференциального исчисления. Теорема Ферма.
Основные теоремы дифференциального исчисления. Теорема Ролля.
Основные теоремы дифференциального исчисления. Теорема Лагранжа.
Основные теоремы дифференциального исчисления. Теорема Коши.
Правило Лопиталя.
Производные высших порядков. Формула Лейбница.
Производные высших порядков. Формула Тейлора.
Общая схема исследования функций. Монотонность функций. Необходимое и достаточное условие монотонности.
Общая схема исследования функций. Экстремум функции. Необходимое условие.
Общая схема исследования функций. Экстремум функции. 1-е и 2-е достаточные условия.
Общая схема исследования функций. Асимптоты графика. Определение. Виды асимптот.
Общая схема исследования функций. Нахождение наклонных асимптот.
Дифференциал длины дуги.
Кривизна кривой. Центр и радиус кривизны.
Определение функции нескольких переменных. Геометрический смысл функции 2-х переменных. Линии и поверхности уровня. Предел функции нескольких переменных.
Непрерывность функции нескольких переменных. Формулировка основных свойств непрерывной функции. Точки, Линии, поверхности разрывов.
Частные производные 1го и высших порядков. Теорема о порядке дифференцирования.
Дифференцирование сложных функций нескольких переменных.
