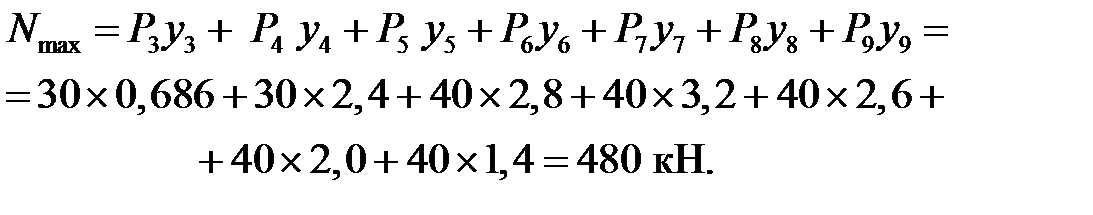Определение опасного положения нагрузки на сооружении по линиям влияния

Основное назначение линий влияния — определение такого положения подвижной нагрузки, при котором исследуемое усилие приобретает максимальное или минимальное значение. Рассмотрим решение этой задачи в общем случае действия на сооружение движущейся связанной системы грузов.

Предположим, что для некоторого усилия построена линия влияния, показанная на рис.12.1, и по сооружению движется поезд, с колес которого на сооружение передаются силы 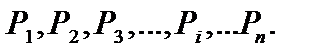Рассмотрим несколько положений поезда.

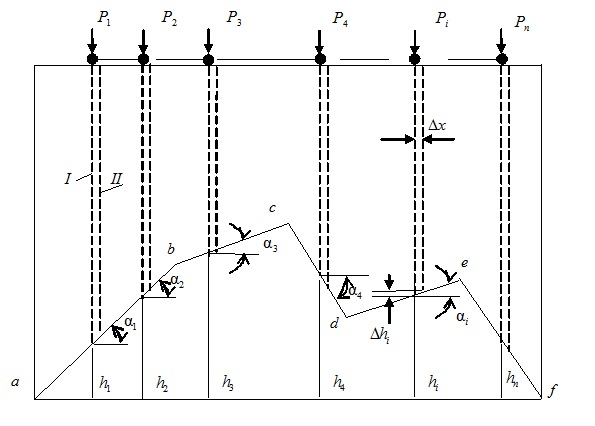
Рис12.1. Линия влияния S

Пусть в положении I ни один из грузов не находится над вершиной линии влияния. Ординаты линий влияния под грузами в этом положении равны 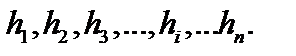Переместим поезд из положения I в положение II на бесконечно малое расстояние 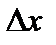. Из рис.12.1 видно, что ордината 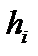под грузом 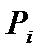изменится на величину 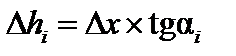. Усилие S при этом получит приращение 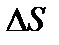, равное

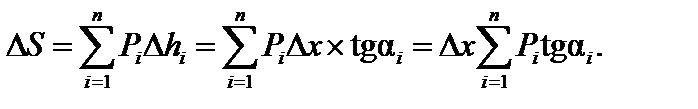(12.1)

При перемещении грузов из положения II в положение III на такое же расстояние (на рис.12.1 положение III не показано) приращение усилия S будет определяься той же формулой (12.1). Если в положении поезда II усилие S имеет максимальное значение, т.е. это положение поезда является опасным для усилия S, то при переходе грузов из состояния I в состояние II приращение усилия 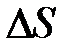будет положительным, а при переходе из состояния II в состояние III—отрицательным.Так как знак приращения усилия определяется знаком суммы 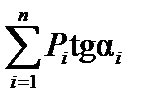, то из приведенных выше рассуждений вытекает, что когда грузы находятся в положении I, знак суммы 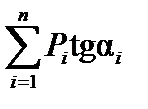должен быть положительным, а когда грузы находятся в положении III, знак суммы 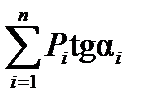должен быть отрицательным. Но это возможно только тогда, когда при переходе из положения I в положение III тангенс угла наклона линии влияния под одним (или несколькими) из грузов уменьшится. Следовательно, в положении II как минимум один из грузов должен находиться над вершиной линии влияния. Этот груз принято называть критическим, а соответствующую вершину линии влияния —критической вершиной. При исследовании на максимум критическая вершина должны быть выпуклой, т.е. для нее должно соблюдаться соотношение 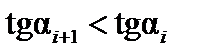, или . 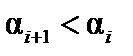Примеры выпуклой и невыпуклой вершин показан на рис.12.2.

Аналогичные рассуждения можно провести при исследовании усилия на минимум. Придем к выводу, что одна и та же вершина при исследовании на максимум может быть выпуклой, а при исследовании на минимум — невыпуклой. Для линии влияния, изображенной на рис.12.1, вершины b, c и e являются выпуклыми, а вершины a,d, иf— невыпуклыми при определении максимума; при определении минимума, наоборот, вершины b, c и e являются невыпуклыми, а вершины a,d, и f— выпуклыми.

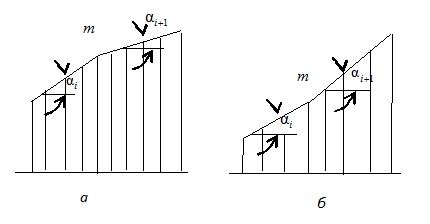
Рис.12.2. Вершина 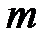: а) выпуклая, б) невыпуклая

Таким образом, при нагружении на максимум сумма 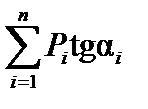должна быть положительной, когда грузы находятся левее опасного положения, и отрицательной, когда правее. При нагружении на минимум сумма 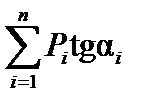должна быть отрицательной, когда грузы находятся левее опасного положения, и положительной, когда правее. В опасном положении один из грузов должен находиться над вершиной линии влияния.

Эти обстоятельства упрощают отыскание опасного положения нагрузки. Рассмотрим пример.

Пусть для некоторого усилия мостовой фермы построена линия влияния, показанная на рис.12.3. Требуется определить максимальное значения этого усилия при движении поезда, нагрузка от которого показана на этом же рисунке, слева направо. При этом:

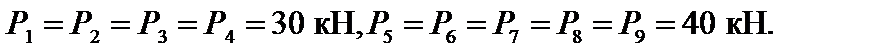
Решение. Находим тангенсы углов наклона для различных участков линии влияния:

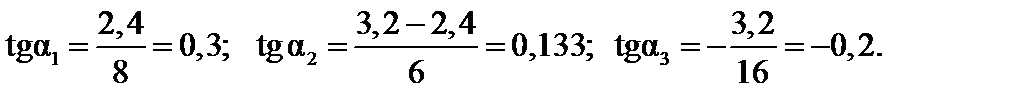
Ищем опасное положение нагрузки, перемещая нагрузку слева направо и помня, что в опасном положении один из грузов должен находиться над выпуклой вершиной линии влияния b или c. При положении всей нагрузки левее точки c 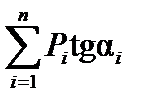не может стать отрицательной при смещении нагрузки вправо на бесконечно малую величину, поэтому перебор различных вариантов начнем со случая, когда груз 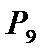встанет над вершинойc, как показано на рис.12.4, а затем весь поезд сдвинется на бесконечно малое расстояние вправо (очевидно, что если нагрузка сдвинется на бесконечно малое расстояние влево, то сумма 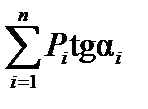останется положительной) .

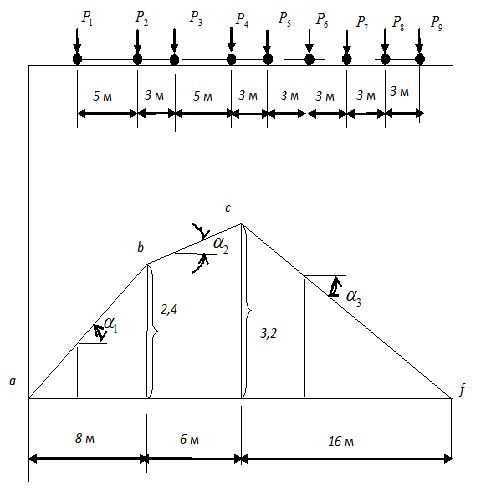
Рис.12.3.Линия влияния N

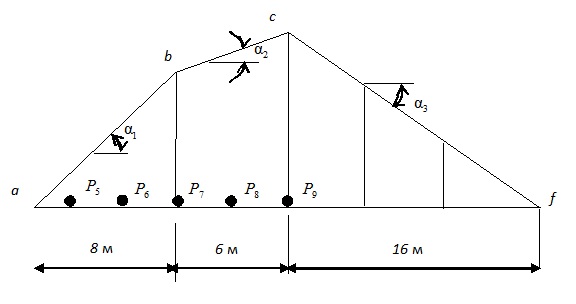
Рис.12.4.Груз Р₉ в вершине c линии влияния

Находим:

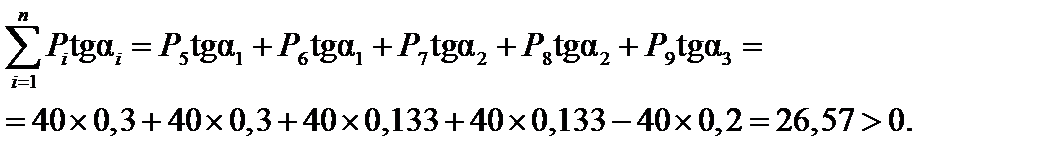
Сумма остается больше нуля, следовательно, груз не является критическим.

Перемещаем поезд вправо таким образом, чтобы груз №8 встал над вершиной с (рис.12.5), затем сдвигаем все грузы на бесконечно малое расстояние вправо и находим:

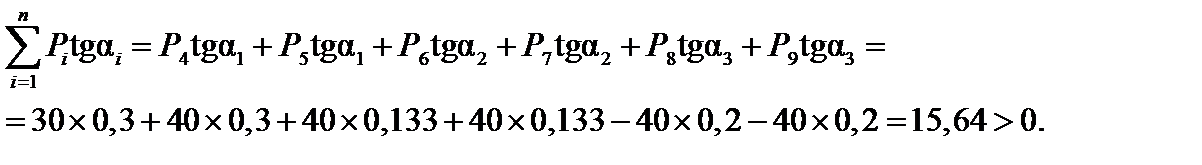
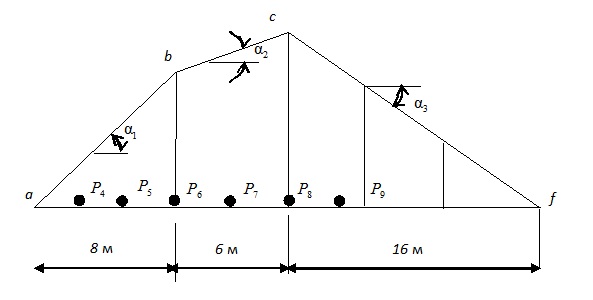
Рис.12.5.Груз Р₈ в вершине c линии влияния

Сумма и в этом случае остается больше нуля, следовательно, груз также не является критическим.

Ставим над вершиной с груз №7 (рис.12.6) и сдвигаем всю нагрузку вправо. Находим:

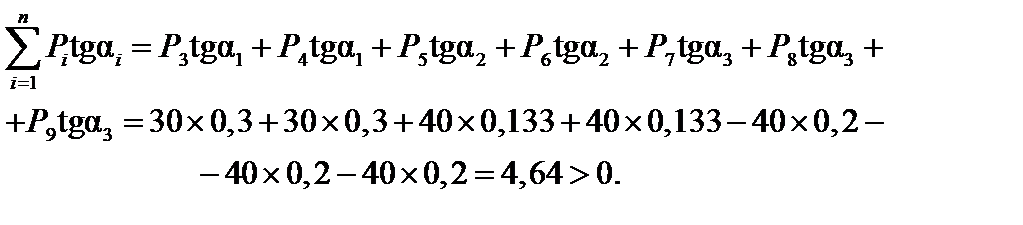
И этот груз не является критическим.

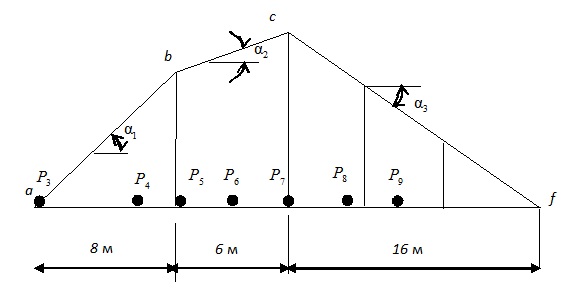
Рис.12.6.Груз Р₇ в вершине c линии влияния

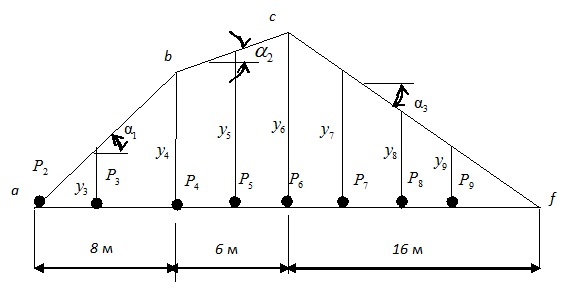
Рис.12.7.Груз Р₆ в вершине c линии влияния

Ставим над вершиной с груз № 6. Сдвигаем все грузы вправо и находим:

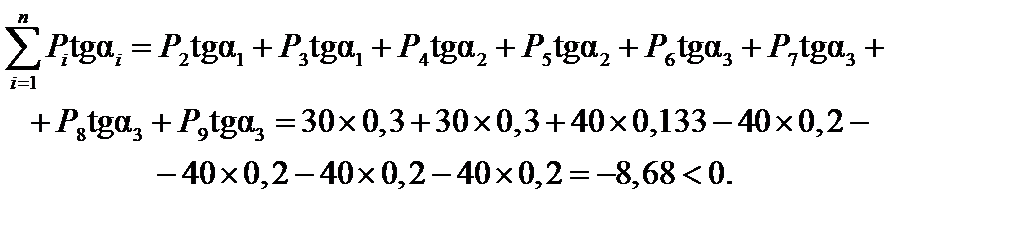
Значение стало отрицательным, следовательно, мы прошли точку экстремума, и груз № 6 является критическим. Положение нагрузки, показанное на рис.12.7, для усилия N является невыгоднейшим (или опасным).

Найдем максимальное значение этого усилия. Для этого из подобия треугольников вычислим ординаты линии влияния под грузами 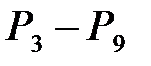(см.рис. 12.7):

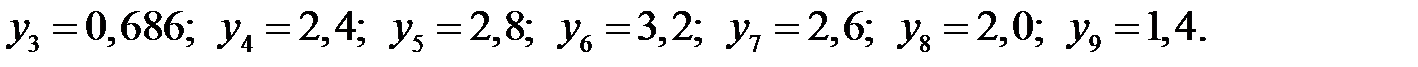
Окончательно получаем: