Цели и задачи строительной механики
Агапов, В.П.
А23 Строительная механика, курс лекций [Электронный ресурс] : учебное пособие / В.П. Агапов ; М-во образования и науки Рос. Федерации, Нац. исследоват. Моск. гос. строит. ун-т. — Электрон. дан. и прогр. (6 Мб). — Москва : НИУ МГСУ, 2015. — Учебное электронное издание: 1 электрон. опт. диск (CD-ROM). — Систем. требования: Intel; Microsoft Windows (XP, Vista, Windows 7); дисковод CD-ROM, 512 Мб ОЗУ; разрешение экрана не ниже 1024×768; ПО Adobe Air, ПО IPRbooks Reader, мышь. — Загл. с титул. экрана
ISBN………………………….
Содержит краткое изложение основ курса строительной механики, необходимых студентам дневного и заочного отделений бакалавриата, для понимания основных принципов и методов расчета стержневых строительных конструкций на прочность. Содержит основные темы дисциплины «Строительная механика»: кинематический анализ сооружений; расчет статически определимых многопролетных балок; расчет статически определимых арок, ферм, рам и др. Теоретический материал сопровождается решением примеров, помогающих лучше усвоить содержание предмета.
Для студентов всех форм обучения по специальности «Промышленное и гражданское строительство» (код направления подготовки 207800).
Учебное электронное издание
Минимальные системные требования: процессор стандартной архитектуры x86
с тактовой частотой от 1,6 ГГц и выше; операционная система Microsoft Windows XP,
Vista или Windows 7; от 512 Мб оперативной памяти;
от 1 Гб свободного пространства на жестком диске;
разрешение экрана не ниже 1024×768; программа Adobe Air.
© НИУ МГСУ, 2015
© Оформление.
ООО «Ай Пи Эр Медиа», 2015
Редактор Е.А. Копылова
Технический редактор А.В. Кузнецова
Корректор А.В. Мисенжников
Компьютерная верстка С.С. Сизиумовой
Дизайн первого титульного экрана Д.Л. Разумного
Для создания электронного издания использовано:
Microsoft Word 2013, приложение pdf2swf из ПО Swftools, ПО IPRbooks Reader,
разработанное на основе Adobe Air
Подписано к использованию 01.09.2015 г. Уч.-изд. л. 3,74. Объем данных 6 Мб,
1 CD-ROM. Тираж 10 экз.
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Национальный исследовательский
Московский государственный строительный университет»
(НИУ МГСУ).
129337, Москва, Ярославское ш., 26.
Издательство МИСИ – МГСУ.
Тел. (495) 287-49-14, вн. 13-71, (499) 188-29-75, (499) 183-97-95.
E-mail: [email protected], [email protected]
ООО «Ай Пи Эр Медиа».
Тел. 8-800-555-22-35, (8452) 24-77-97, вн. 208,
E-mail: [email protected], [email protected]
www.iprbookshop.ru
ОГЛАВЛЕНИЕ
Лекция 1
1.1. Цели и задачи строительной механики
1.2. Опоры. Конструкции опор и их условные обозначения
1.3. Кинематический анализ сооружений
Лекция 2
СТАТИКА СООРУЖЕНИЙ
1. Общие понятия
1.1.Расчетная схема сооружения
1.2.Классификация стержневых систем
2. Статически определимые системы
2.1. Общие правила определения усилий для всех типов статически определимых конструкций
2.2.Частные случаи определения усилий
3. Пример расчета многопролетной статически определимой балки
Лекция 3
1. Определение усилий в трехшарнирных арках и рамах
1.1.Определение опорных реакций
1.2.Определение внутренних усилий
2.Примеры расчета трехшарнирной арки
Лекция 4
1. Определение усилий в стержнях ферм
1.1.Способ вырезания узлов
1.2. Способ разрезов
Лекция 5
1. Определение усилий в статически определимых рамах
Лекция 6
1.Определение перемещений в стержневых системах от силового воздействия
2.Определение температурных перемещений в стержневых системах
3. Определение перемещений от смещения опор
Лекция 7
Примеры определения перемещений в стержневых системах
Лекция 8
1. Определение перемещений в арках
2. Определение перемещений в фермах
Лекция 9
1. Определение температурных перемещений
2. Определение перемещений, вызванных осадкой опор
Лекция 10
1.Расчет стержневых систем на подвижную нагрузку. Общая теория линий влияния
1.1. Линии влияния для простой балки
Лекция 11
1. Определение усилий по линиям влияния
2. Построение линий влияния для многопролетных балок
3. Построение линий влияния для трехшарнирных арок
Лекция 12
1. Определение опасного положения нагрузки на сооружении по линиям влияния
Лекция 13
1. Расчет статически неопределимых систем методом сил
2. Канонические уравнения метода сил
Лекция 14
1.Примеры расчета рам методом сил
1.1. Расчет на действие силовой нагрузки
1.2. Расчет на действие температуры
1.3.Расчет на заданное смещение опор
2.Таблица эпюр моментов и поперечных сил в однопролетных статически неопределимых балках
Лекция 15
1. Примеры расчета рам методом сил (продолжение)
Лекция 16
1.Расчет симметричных рам на действие симметричных и обратно симметричных нагрузок
2. Преобразование произвольной нагрузки к прямо и обратно симметричному виду
3. Определение перемещений от силовой нагрузки в статически неопределимых рамах.
Лекция 17
1.Расчет стержневых систем методом перемещений
1.1.Выбор и определение числа неизвестных
1.2.Основная система. Канонические уравнения метода перемещений
1.3.Определение коэффициентов и свободных членов системы канонических уравнений метода перемещений
Лекция 18
1. Пример расчета рамы методом перемещений
Лекция 19
1. Пример расчета рамы методом перемещений на действие температуры
Лекция 20
1. Матричная форма метода перемещений
1.1.Матрица жесткости стержня
Лекция 21
1. Переход к глобальной системе координат
2. Матрица жесткости конструкции
3. Алгоритм расчета конструкций методом перемещений в матричной форме
4. Реализация матричной формы метода перемещений на ЭВМ
Лекция 22
1. Пример расчета фермы матричным способом
ЛЕКЦИЯ 23
1. Пример расчета рамы методом перемещений по программе ПРИНС
Список рекомендуемой литературы
ЛЕКЦИЯ 1. ОБЩИЕ ПОЛОЖЕНИЯ
ОБЩИЕ ПОНЯТИЯ
РАСЧЕТНАЯ СХЕМА СООРУЖЕНИЯ
Расчетной схемой сооружения называется ее упрощенное изображение. Упрощения достигаются отбрасыванием второстепенных факторов, мало влияющих на результаты расчета. Элементы стержневых систем изображаются на расчетных схемах своими осями.
По кинематическому признаку
По кинематическому признаку сооружения делятся на статически определимые и статически неопределимые.
ЧАСТНЫЕ СЛУЧАИ ОПРЕДЕЛЕНИЯ УСИЛИЙ
ПРИМЕР РАСЧЕТА МНОГОПРОЛЕТНОЙ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ
Пример1: Построить эпюры изгибающих моментов и поперечных сил для балки, изображенной на рис.2.13, а.
Решение:
Конструкция состоит из двух балок 1-3 и 3-6. Балка 1-3 является основной, так как она может самостоятельно нести приложенные к ней нагрузки. Балка 3-6 является подвесной. В точке 3 она опирается на основную балку и имеет одну опору в точке 5. Схема взаимодействия балок (поэтажная схема) приведена на рис.2.13,б.
Расчет начинаем с верхней на поэтажной схеме балки 3-6. Эпюры изгибающих моментов и поперечных сил для этой балки, полученные методами сопротивления материалов, приведены на рис.2.13,в. При этом предварительно были найдены реакции балки 3-6 на опоре 3. На втором этапе рассчитываем балку 1-3, приложив к ней наряду с заданными внешними силами давление, которое передается с вышележащей балки3-6. Это давление равно взятой с обратным знаком реакции балки 3-6 на опоре 3. Результаты расчета балки 1-3 приведены на рис. 2.13,г. Чтобы получить окончательные результаты для заданной многопролетной балки, необходимо объединить эпюры, полученные для составляющих простых балок.
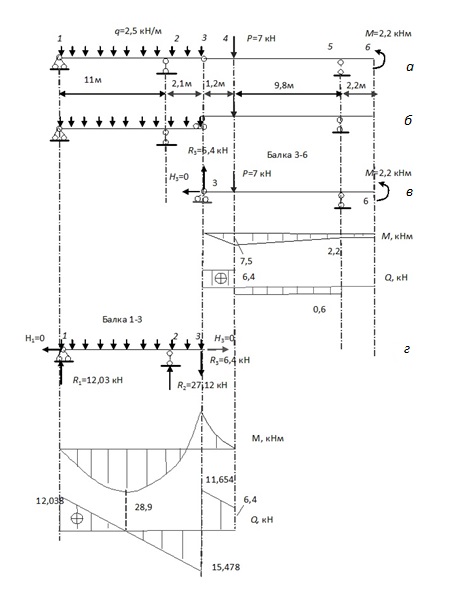
Рис.2.1. К расчету составной балки: а – заданная балка, б – поэтажная схема, в – подвесная балка, г – главная балка
ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ
В трехшарнирных системах при действии вертикальной нагрузки на опорах возникают, как правило, вертикальные и горизонтальные реакции. Поэтому эти системы принято называть распорными. Рассмотрим методику определения опорных реакций.
Пусть трехшарнирная арка нагружена, как показано на рис. 3.3.
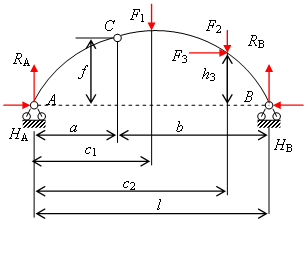
Рис.3.3. К определению опорных реакций
Вертикальные составляющие опорных реакций могут быть найдены так же, как и в простой балке на двух опорах, из уравнений равновесия в виде суммы моментов всех сил относительно опорных точек. В данном случае эти уравнения имеют вид:
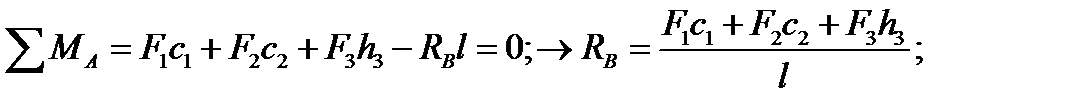
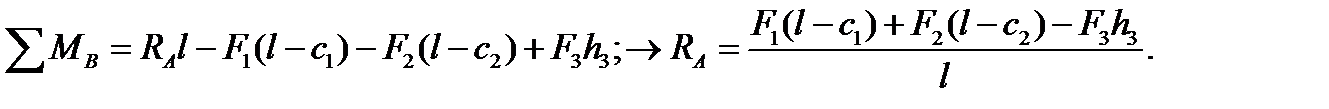
Горизонтальные составляющие опорных реакций могут быть найдены из условия равенства нулю изгибающего момента в шарнире С.Вычисляя момент в шарнире С через левые силы, получаем:
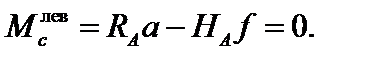 Отсюда Отсюда 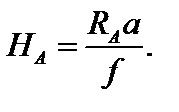 | (3.1) |
Выражая момент в шарнире С через правые силы, находим:
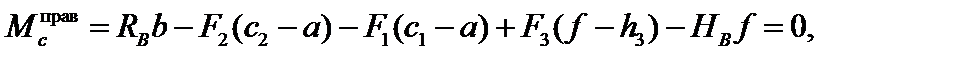 | (3.2) |
отсюда
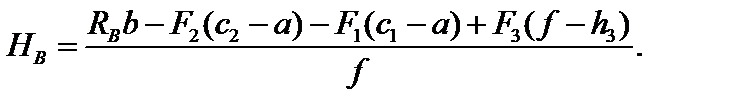 | (3.2) |
При действии только вертикальных нагрузок (в рассматриваемом примере при F3=0) формулы (3.1) и (3.2) принимают вид:
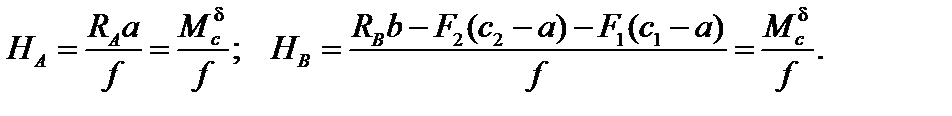 | (3.3) |
В формулах (3.3) через 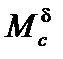 обозначен изгибающий момент в простой балке, перекрывающей такой же пролет и нагруженной такими же силами, как и арка.
обозначен изгибающий момент в простой балке, перекрывающей такой же пролет и нагруженной такими же силами, как и арка.
Очевидно, что в этом случае 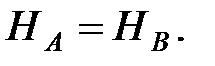 Горизонтальная реакция в трехшарнирной арке называется распором и обозначается буквой H. Из формул (3.3) получаем:
Горизонтальная реакция в трехшарнирной арке называется распором и обозначается буквой H. Из формул (3.3) получаем:
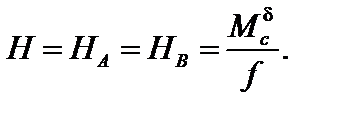 | (3.4) |
ПРИМЕРЫ РАСЧЕТА ТРЕХШАРНИРНОЙ АРКИ
Пример 1.
Для сплошной трехшарнирной арки (рис.3.5) требуется определить аналитически изгибающие моменты, поперечные и продольные силы в сечениях к1 и к2 от действия постоянной заданной нагрузки.
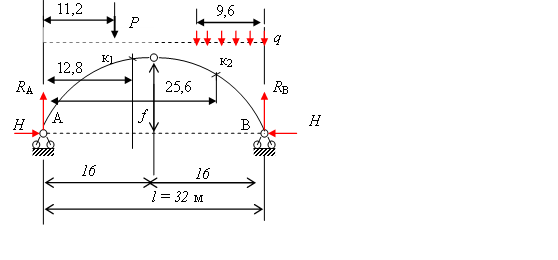
Рис.3.5.К примеру 1
Дано: ℓ = 32м;q = 6кН/м;f/ℓ = 0,35; Р = 3кН.
Очертание оси арки — окружность:
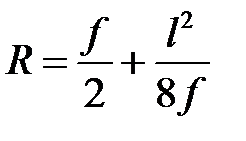 ,
,
где R— радиус окружности, по которой очерчена арка.
Уравнение оси:
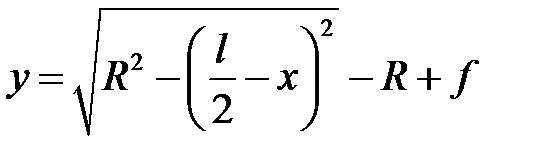 ;
;
Функции угла наклона касательной: 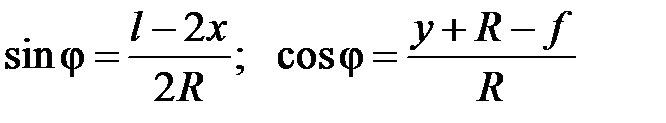 .
.
Решение:
1) Вычисление геометрических характеристик:
f = 0,35ℓ = 0,35 × 32 = 11,2 м;
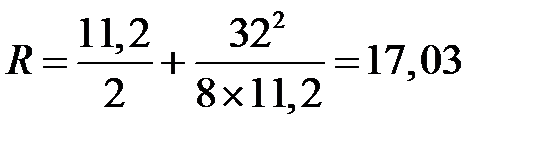 м;
м;
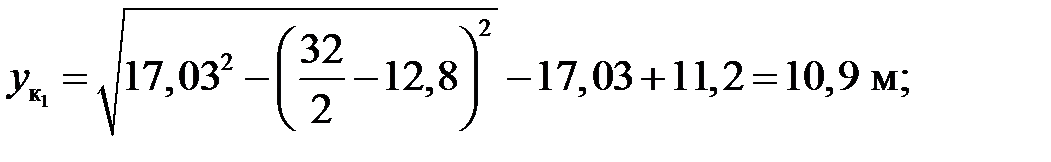
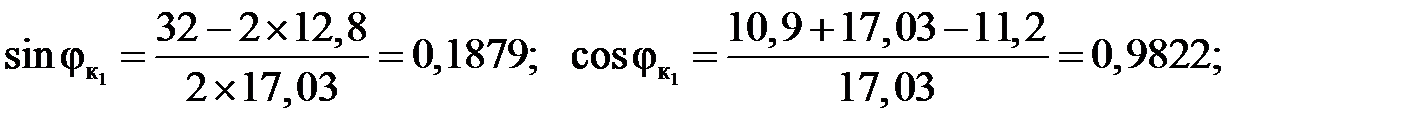
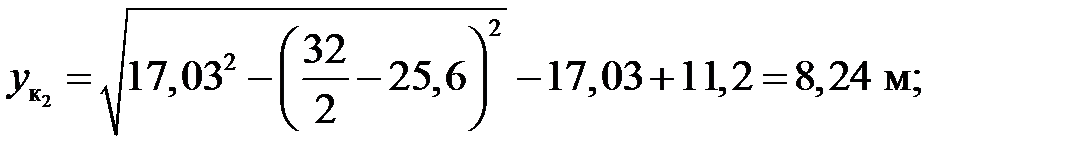
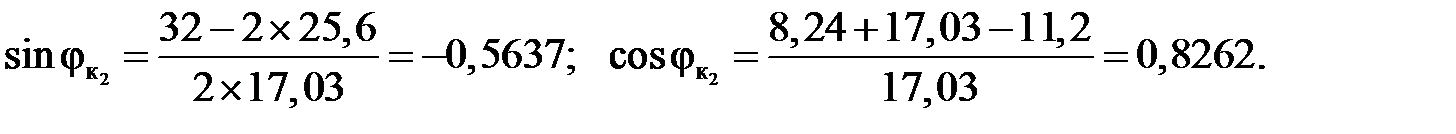
2) Вычисление опорных реакций:
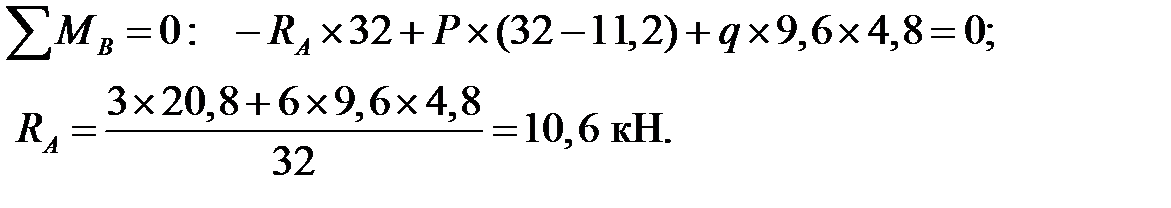
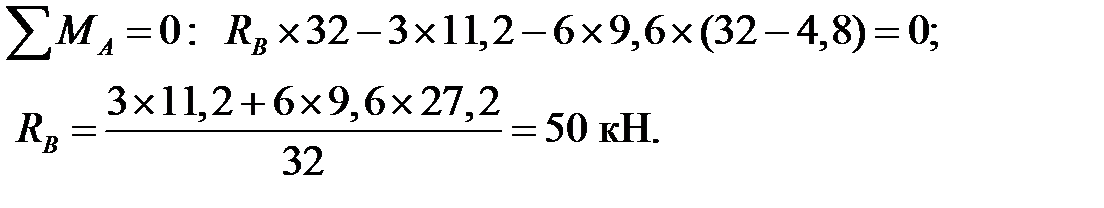
Проверка:
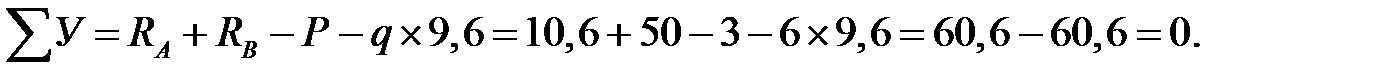 Вертикальные реакции найдены верно.
Вертикальные реакции найдены верно.
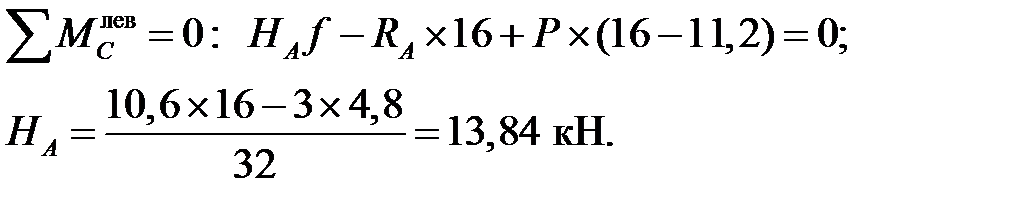
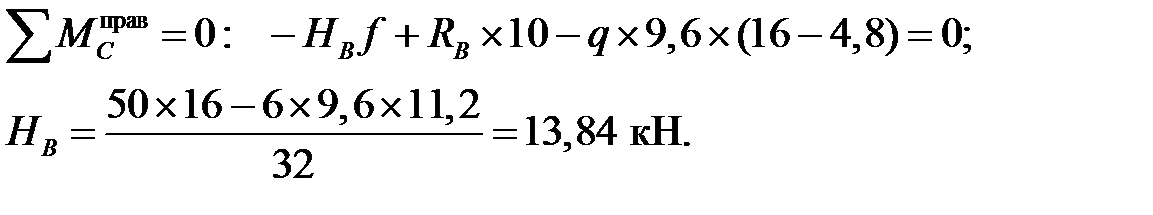
Поверка:
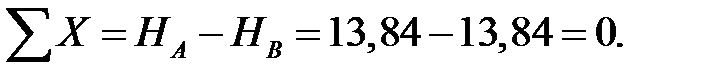
Горизонтальные реакции найдены верно.
3) Вычисление внутренних усилий:
балочные значения:
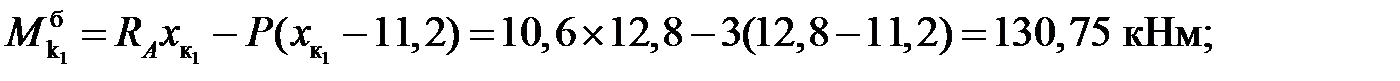
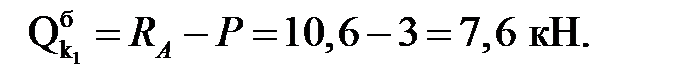
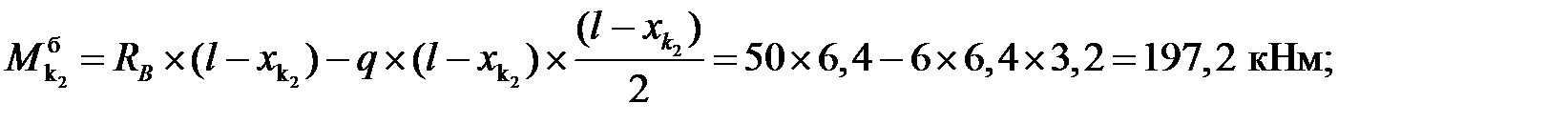
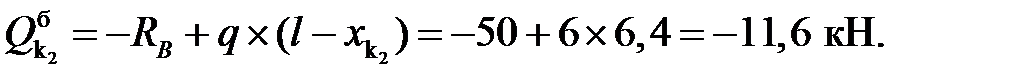
Усилия в сечениях арки:
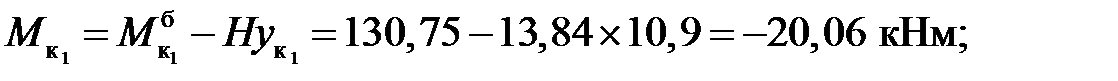
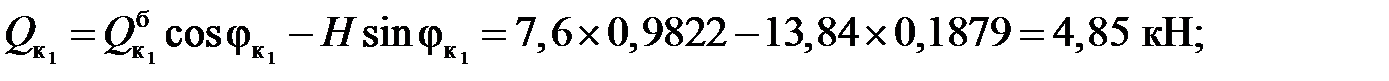
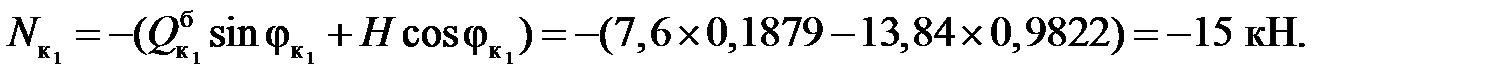
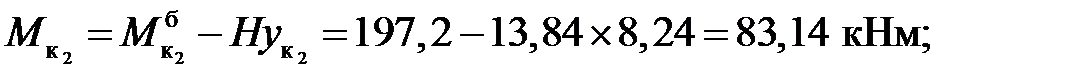
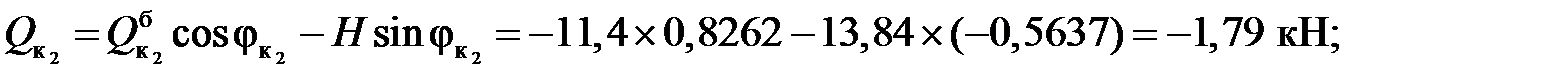
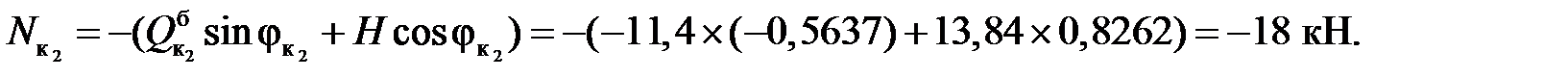
Пример2. Определить изгибающие моменты, поперечные и продольные силы в сечениях к1 и к2 арки (рис.3.6) от действия заданной нагрузки.
Дано: Р= 6 кН,q=4 кН/м, l=20 м, f=6 м, ось арки — парабола.
Уравнение оси:
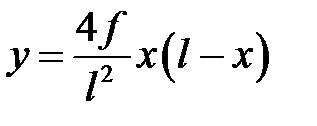 .
.
Решение.
1. Вычисление геометрических характеристик сечений.
По уравнению оси находим:
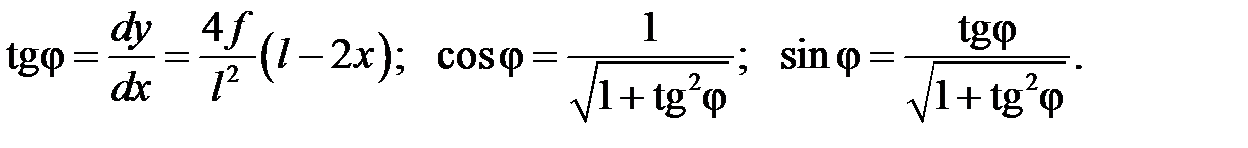
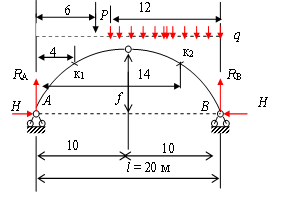
Рис.3.6. К примеру 2
Ординаты сечений:
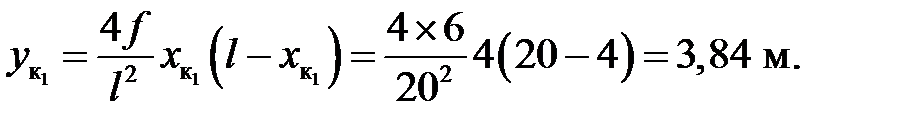
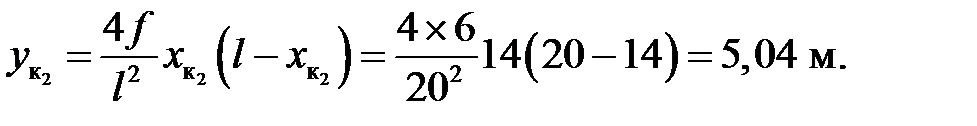
Характеристики углов наклона касательных к оси:
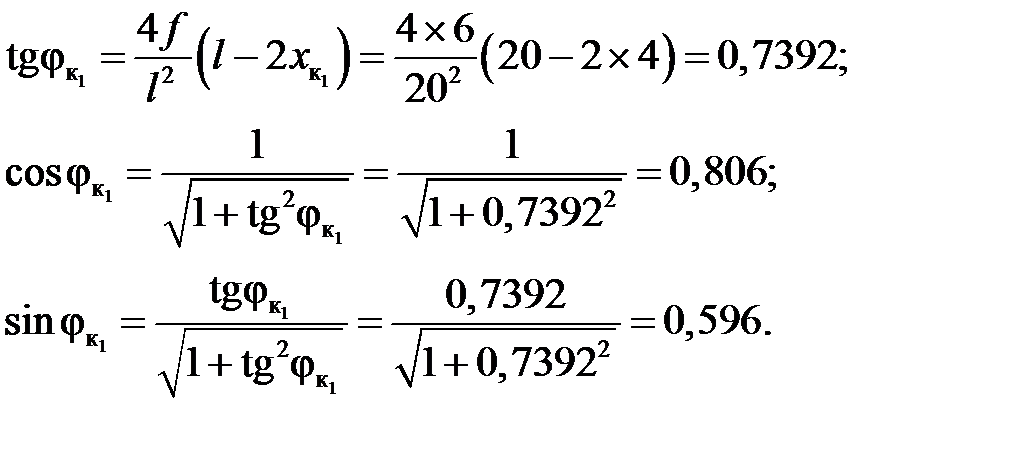
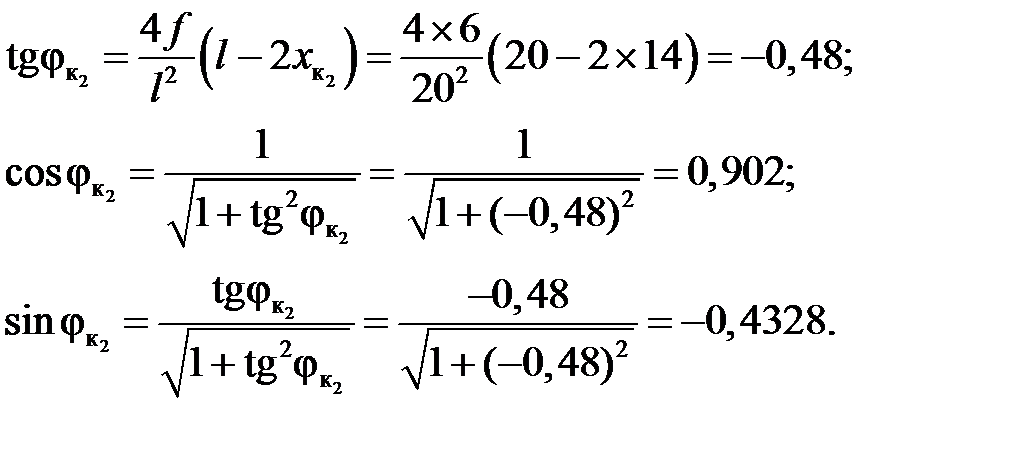
2. Определение опорных реакций:
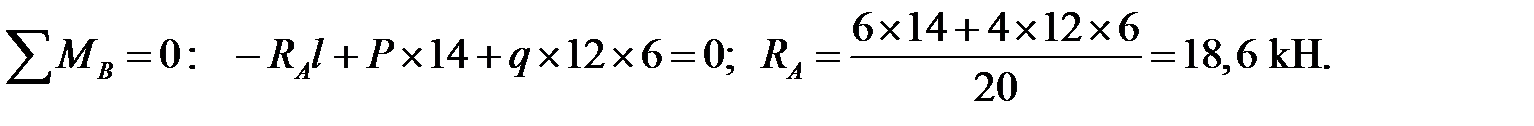
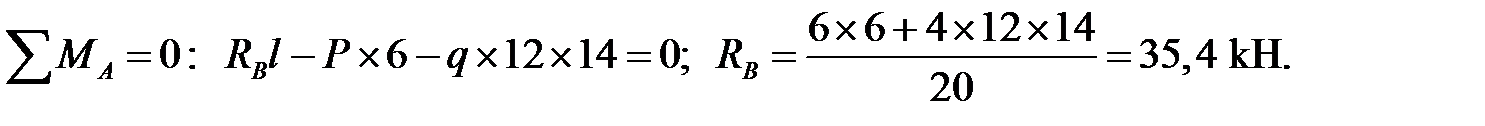
Проверка:
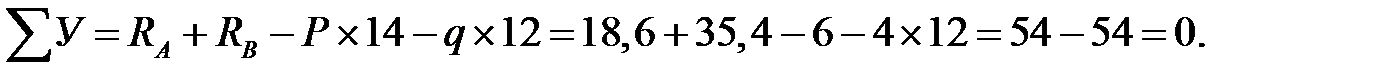
Вертикальные реакции найдены верно.
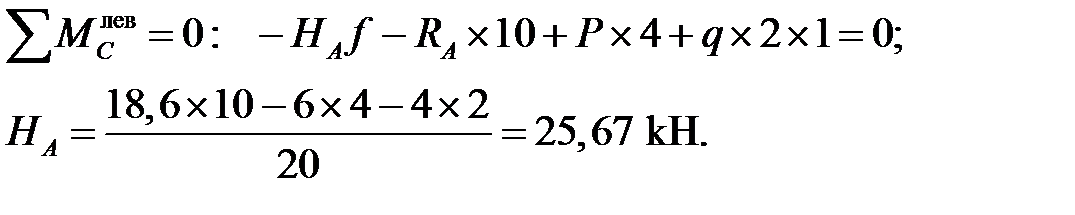
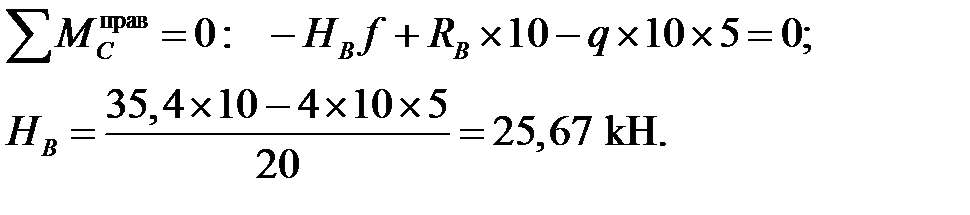
Поверка:
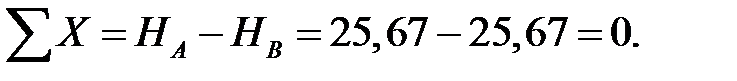
Горизонтальные реакции найдены верно.
3. Вычисление внутренних усилий:
балочные значения:
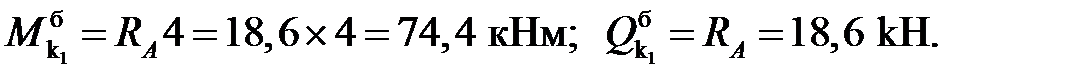
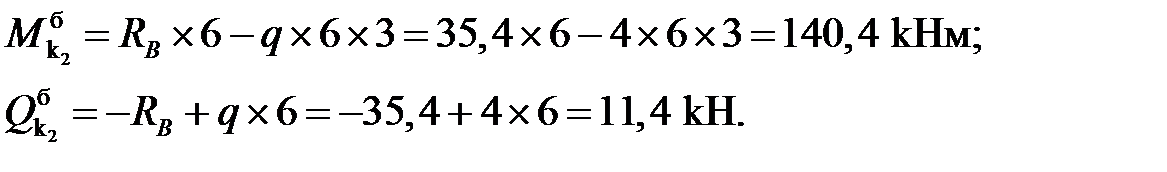
Усилия в сечениях арки:
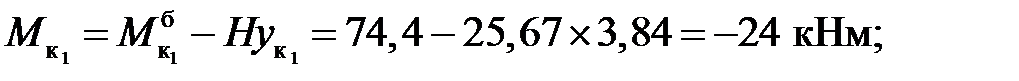
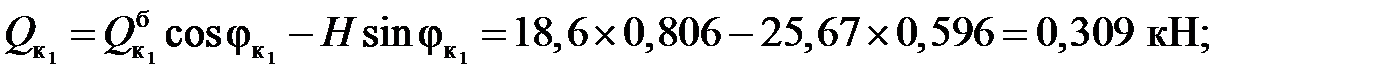
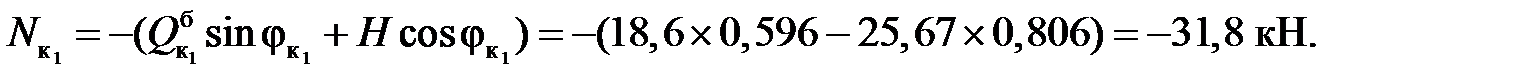
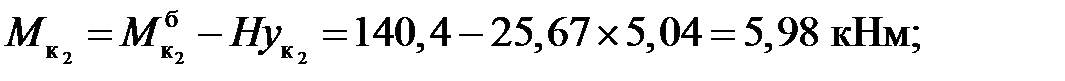
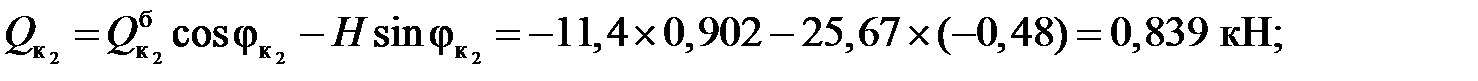
ЛЕКЦИЯ 4. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ
СПОСОБ ВЫРЕЗАНИЯ УЗЛОВ
При реализации этого способа последовательно вырезаются узлы фермы и для каждого из них составляются уравнения равновесия в виде суммы проекций всех внешних и внутренних сил, действующих на данный узел, на две не параллельные друг другу оси. В общем случае получается система из 2У уравнений равновесия, из которых и могут быть найдены С+С0 усилий как в стержнях фермы, так и в опорных стержнях. Всегда, однако, можно выбрать такую последовательность вырезания узлов, при которой каждый раз нужно будет решать не более двух уравнений с двумя неизвестными. Начинать нужно с того узла, в котором сходится не более двух стержней с неизвестными усилиями. Например, при расчете фермы рис. 4.1 необходимо начать с узла 1, в котором сходится два стержня. Вырежем этот узел (рис.4.2) и составим для него уравнения равновесия.
Усилия в стержнях можно обозначать по-разному. Рекомендуем обозначать их буквой N с индексами, показывающими, к каким узлам прикреплен данный стержень. При этом неизвестное усилие рекомендуется считать растягивающим. Знак минус у результата будет означать, что стержень на самом деле сжат.
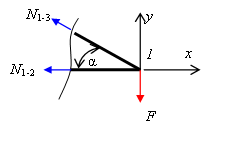
Рис.4.2. Узел 1
В рассматриваемом примере N1-3 можно сразу найти из уравнения проекции на ось y:
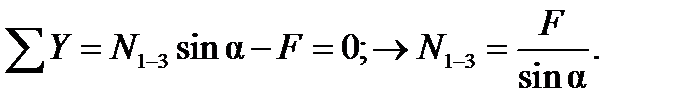
Усилие N1-2 можно найти теперь из уравнения проекций на ось x:
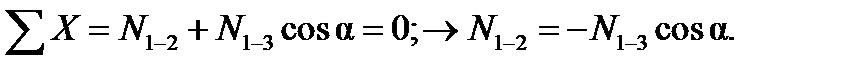
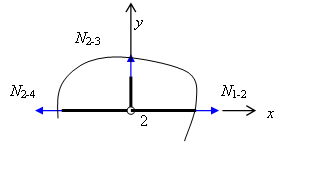
Рис.4.3. Узел 2
Вырежем узел 2 (рис. 4.3). Из уравнения проекций на ось y находим:
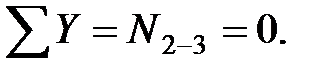
Из уравнения проекций на ось X получаем:
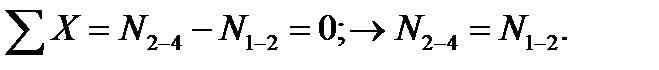
Действуяаналогичным образом, можно найтиусилия во всех стержнях, в том числе и опорных. Заметим, что, если бы мы попытались после первого узла сразу перейти к третьему, то получили бы для этого узла два уравнения с тремя неизвестными 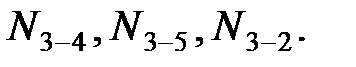 Заметим также, что усилие в стержне 2-3 равно нулю, и возникает вопрос о целесообразности использования этого стержня в данной конструкции. В общем случае включение подобных стержней в состав конструкции объясняется конструктивными соображениями, например, стремлением собрать конструкцию из более коротких стержней, которые, к тому же оказываются и более устойчивыми.
Заметим также, что усилие в стержне 2-3 равно нулю, и возникает вопрос о целесообразности использования этого стержня в данной конструкции. В общем случае включение подобных стержней в состав конструкции объясняется конструктивными соображениями, например, стремлением собрать конструкцию из более коротких стержней, которые, к тому же оказываются и более устойчивыми.
При расчете способом вырезания узлов ферм на двух опорах (см. рис. 4.4), необходимо в первую очередь найти опорные реакции.
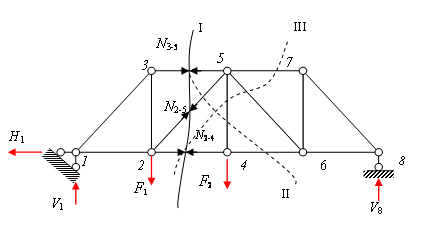
Рис.4.4. Ферма на двух опорах
Отметим, что при определении усилий в стержнях статически определимых ферм полезно помнить приведенные ниже правила, не требующие доказательств (леммы).
Лемма 1. Если в конструкции фермы имеется трехстержневой узел, в котором два стержня лежат на одной прямой, а третий, называемый одиночным, — под углом к ним, и если в узле приложена внешняя сила, направленная вдоль одиночного стержня, то усилия в первых двух стержнях равны между собой, а усилие в одиночном стержне равно внешней силе.
Лемма 2. Если в ненагруженном трехстержневом узле фермы имеется одиночный стержень, то усилие в этом стержне равно нулю.
СПОСОБ РАЗРЕЗОВ
При использовании этого способа ферма мысленно рассекается на две части, одна часть отбрасывается, действие ее заменяется силами, и для оставшейся части составляются три уравнения равновесия. Разрез нужно проводить так, чтобы в него попало не более трех стержней с неизвестными усилиями. Уравнения равновесия целесообразно составлять таким образом, чтобы они решались независимо друг от друга. Это всегда можно сделать, если придерживаться приведенного выше правила разрезания фермы. Так, если три стержня, попавшие в разрез, не параллельны друг другу, то для определения усилий в одном из них можно составить уравнения равновесия в виде суммы моментов всех сил, действующих на отсеченную часть, относительно точки пересечения двух других стержней. Эта точка называется моментной точкой, а сам способ составления уравнений равновесия —способом моментной точки.
Если два стержня из трех, попавших в разрез, параллельны между собой, а третий расположен под углом к ним, то для определения усилия в наклонном стержне уравнения равновесия следует составлять в виде равенства нулю сумм проекций всех сил, действующих на отсеченную часть фермы, на направление, перпендикулярное двум параллельным стержням. Такой способ составления уравнений равновесия называется способом проекций.
Проиллюстрируем сказанное примерами.
Пример 1.
Найдем усилия в стержнях второй панели слева фермы, изображенной на рис.4.4. Проведем сечение I (попытки проведения сечения II или сечения III, как показано на рис. 4.4 пунктиром, следует признать неудачными, т.к. они проходят через четыре стержня с неизвестными усилиями). Для определения усилия N3-5 выберем моментную точку в узле 2и составим для левой отсеченной части уравнения моментов относительно этой точки. Получим:
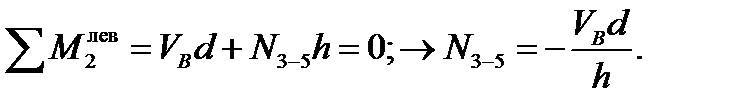
Для определения усилия в стержне 2-5 составим уравнения равновесия любой отсеченной части в виде суммы проекций всех сил на вертикальную ось:
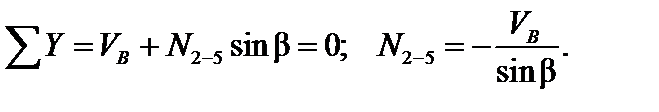
Пример 2.
Для фермы, изображенной на рис.4.5, найдем усилия в стержнях второй панели слева, включая обе стойки, при следующих данных: d=3 м, h =4 м, Р=4 кН.
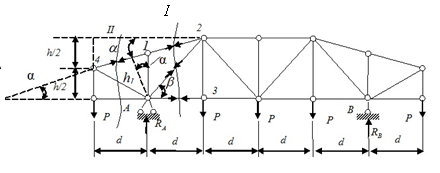
Рис.4.5. К примеру 2
Решение.
1. Определение опорных реакций.
Ввиду симметрии схемы конструкции и приложенной нагрузки опорные реакции в данном случае равны между собой, т.е.:
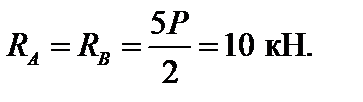
2.Определение внутренних усилий.
Усилия в стойках находим на основании леммы 1. Получаем:
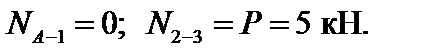
Усилие в стержне А-3 находим методом моментной точки. В качестве моментной точки принимаем точку пересечения стержней 1-2 и А-2. Проводим сечение I и составляем уравнение равновесия левой отсеченной части фермы в виде суммы моментов всех сил относительно точки 2:
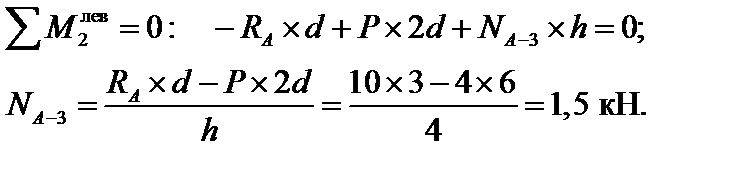
Усилие в стержне 1-2 также найдем методом моментной точки. В качестве моментной точки выберем узел А. Получим:
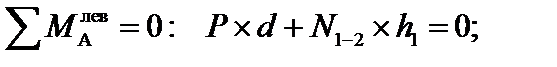
Чтобы воспользоваться полученным уравнением, необходимо найти плечо усилия 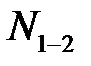 , т.е. длину перпендикуляра
, т.е. длину перпендикуляра 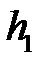 , опущенного из моментной точки А на направление усилия
, опущенного из моментной точки А на направление усилия 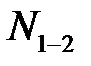 . Эта задача решается геометрическим путем. Очевидно, что:
. Эта задача решается геометрическим путем. Очевидно, что:
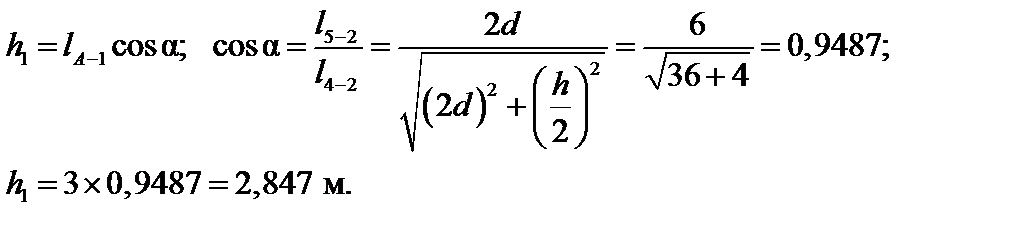
Подставляя значение 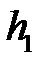 в уравнение равновесия, находим:
в уравнение равновесия, находим:
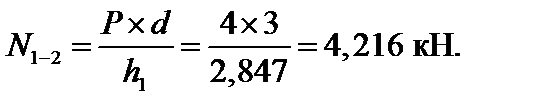
Усилие в стержне А-2 находим методом проекций:
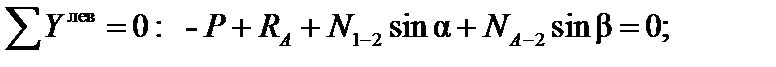
Отсюда:
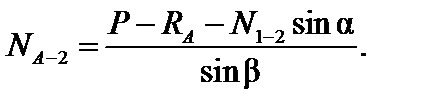
Значение sinβнаходим из прямоугольного треугольника А-3-2, а значение sinα— из треугольника 4-5-2:
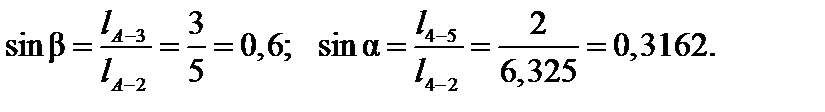
Окончательно получаем:
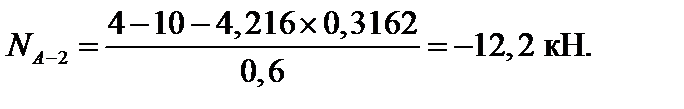
Таким образом, определение усилий в стержнях статически определимых ферм не представляет больших трудностей. В данной лекции описаны два метода: метод вырезания узлов и метод разрезов, хотя, по сути дела, речь идет о модификациях одного и того же универсального метода — метода сечений. Разделяя способы, автор следует здесь традиции, установившейся в строительной механике стержневых систем.
Растяжение-сжатие
Внутренние силы,соответствующие растяжению или сжатию,показаны на рис.6.3.
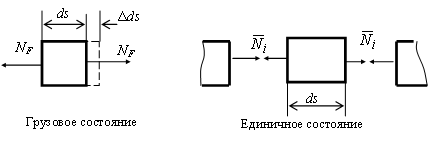
Рис.6.3. Внутренние силы, соответствующие растяжению (сжатию)
Удлинение элемента ds в грузовом состоянии равно:
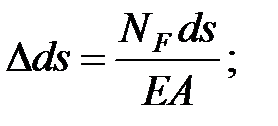
Работа внутренней продольной силы единичного состояния на этом перемещении равна:
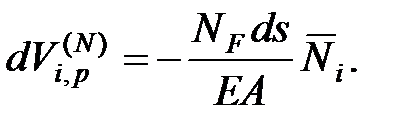 | (6.3) |
Кручение
Внутренние силы, соответствующие кручению, показаны на рис.6.4.
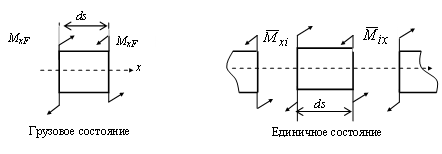
Рис.6.4. Внутренние силы, соответствующие кручению
Угол закручивания элемента ds в грузовом состоянии равен:
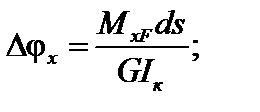
Работа внутреннего крутящего момента единичного состояния на этом перемещении равна:
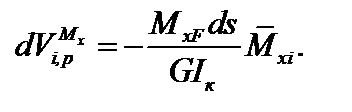 | (6.4) |
Изгиб в плоскости xoy
Найдем работу изгибающих моментов 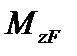 (рис.6.5).
(рис.6.5).
Взаимный угол поворота сечений элемента ds в грузовом состоянии определяется формулой (см. курс сопротивления материалов):
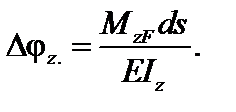
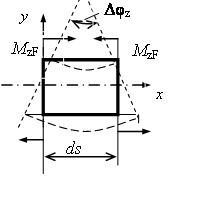
Рис.6.5.Изгиб в плоскости xoy
Работа внутренних изгибающих моментов единичного состояния на данном перемещении равна:
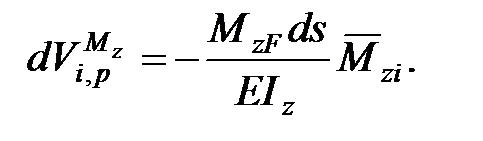 (6.5)
(6.5)
Аналогично для плоскости xoz:
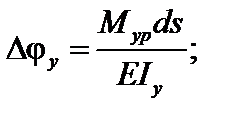
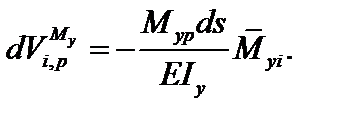 (6.6)
(6.6)
Сдвиг в плоскости xoy
Угол сдвига в плоскости xoy элемента ds, обусловленный действием поперечной силы Qy,(рис.6.6) определяется по закону Гука: 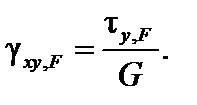 Сдвиг правой грани элемента относительно левой приводит к ее линейному смещению на величину:
Сдвиг правой грани элемента относительно левой приводит к ее линейному смещению на величину:
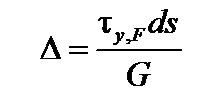 . . | (6.7) |
Рис.6.6. К определению работы поперечной силы 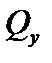
На элемент площади dA в единичном состоянии действует сила 
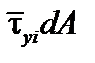 . Работа силы
. Работа силы 
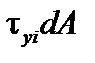 в пределах площадки dA равна:
в пределах площадки dA равна:
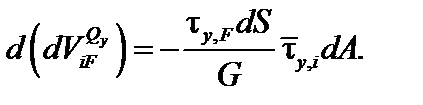 | (6.8) |
Работа сил 
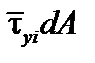 в пределах всего сечения:
в пределах всего сечения:
 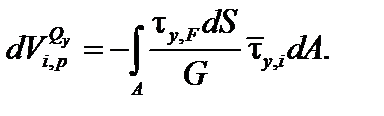 | (6.9) |
Согласно формуле Журавского 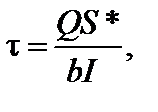 следовательно:
следовательно:
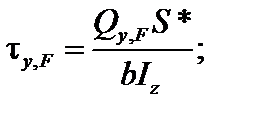 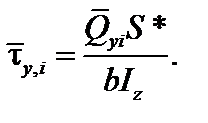 | (6.10) |
Тогда:
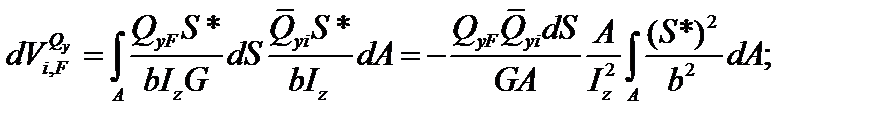 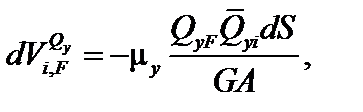 где где 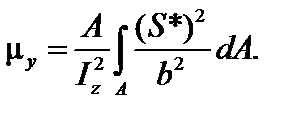 | (6.11) | ||
Аналогично для плоскости xoz имеем: 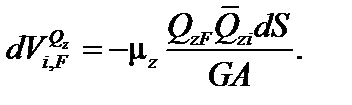 | (6.12) | ||
Работа ViF для всей конструкции:
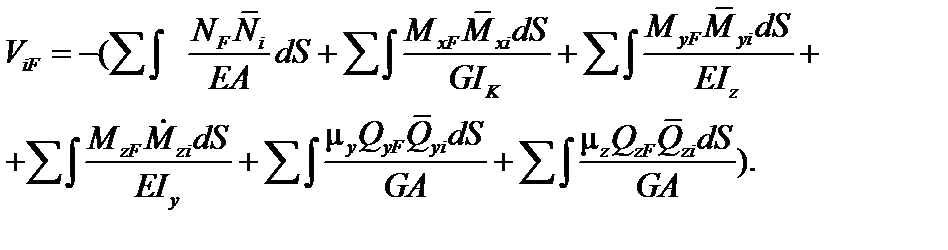 | (6.13) |
Подставляя Ai,F и ViFв формулу (6.1), находим:
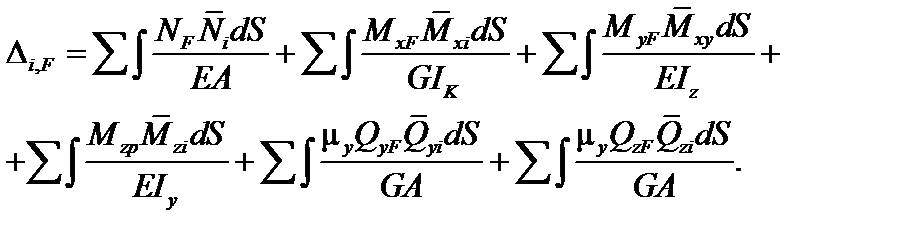 | (6.14) |
Таким образом, получена универсальная формула для вычисления перемещений от силового воздействия в стержневых системах. Эта формула называется формулой или интегралом Мора (по имени автора).
При расчете плоских стержневых систем можно пренебречь слагаемыми, определяемыми продольными и поперечными силами (ввиду их небольшого вклада). В этом случае интеграл Мора записывается в виде:
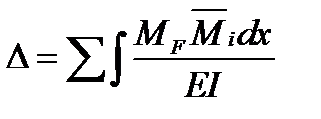 .
.
При определении перемещений в шарнирно-стержневых системах (фермах) в этой формуле остается только одно слагаемое:
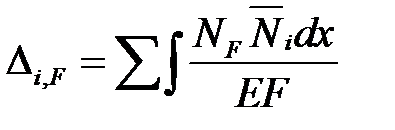 ,
,
Если продольная сила по длине стержней не меняется, то формула принимает вид:
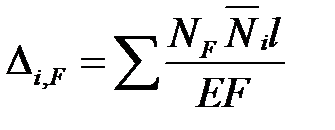 .
.
Формула Мора для конструкций, работающих на изгиб (при условии, что жесткости стержней по длине стержней не изменяются), записывается так:
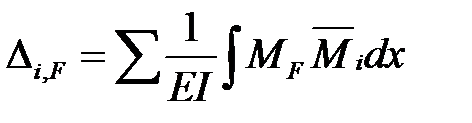
Правила вычисления интеграла Мора:
По Верещагину:
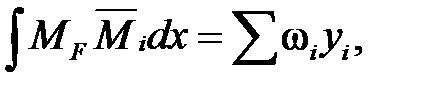
где площадь грузовой эпюры, 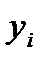 — ордината единичной эпюры, взятая под центром тяжести грузовой.
— ордината единичной эпюры, взятая под центром тяжести грузовой.
По формуле Симпсона:
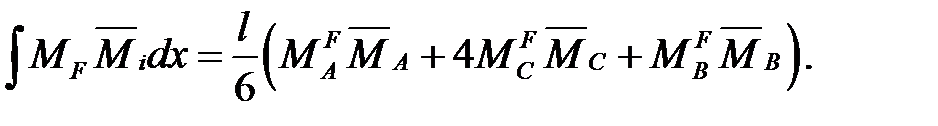

ЛЕКЦИЯ 7. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Пример 1. Найти прогиб в сечении 4 и угол поворота в сечении 2 составной балки (рис.7.1,а) при следующих исходных данных:
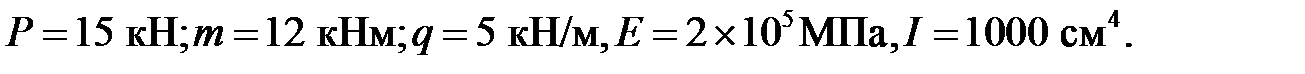
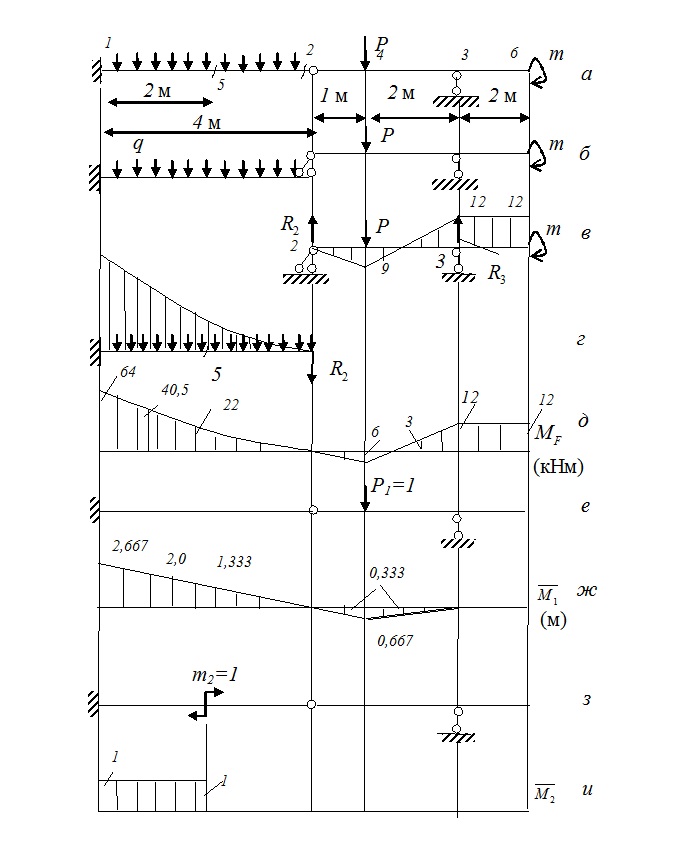
Рис.7.1. К примеру 1
Решение.
1. Построение грузовой эпюры моментов
1.1) Строим поэтажную схему (см. рис.7.1,б).
1.2) Проводим расчет вспомогательной балки 2-3 (рис.7.1,в).
Определение опорных реакций:
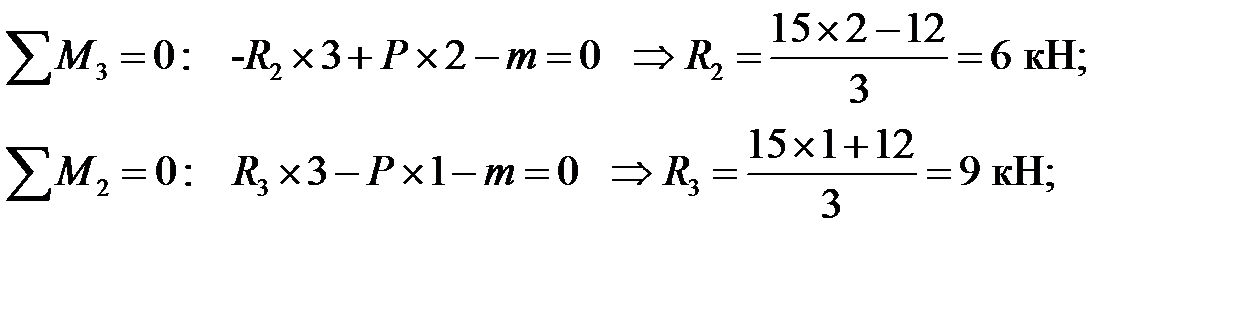
Проверка: 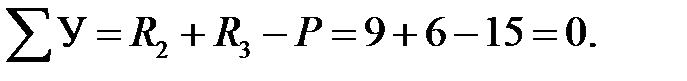
Определение изгибающих моментов:
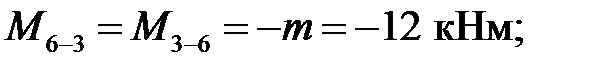
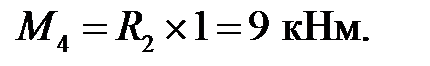
Cхема вспомогательной балки и эпюра изгибающих моментов для нее приведены на рис.7.1,в.
1.3) Рассчитываем главную балку 1-2.
Консольную балку можно рассчитать, не определяя опорных реакций. Находим изгибающие моменты:
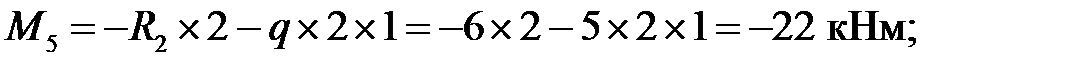
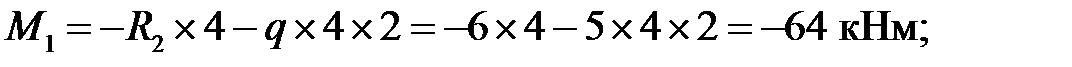
Cхема главной балки и эпюра изгибающих моментов для нее приведены на рис.7.1,г.
1.4) Объединяем эпюры изгибающих моментов, построенные для каждой балки в отдельности, и получаем грузовую эпюру изгибающих моментов для составной конструкции.
2. Для определения прогиба в точке 4 приложим в этой точке единичную силу, как показано на рис.7.1,е, и построим эпюру изгибающих моментов 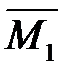 от этой силы (см. рис.7.1,ж; промежуточные расчеты опущены).
от этой силы (см. рис.7.1,ж; промежуточные расчеты опущены).
3. Находим прогиб по формуле Мора (используем формулу численного интегрирования Симпсона):
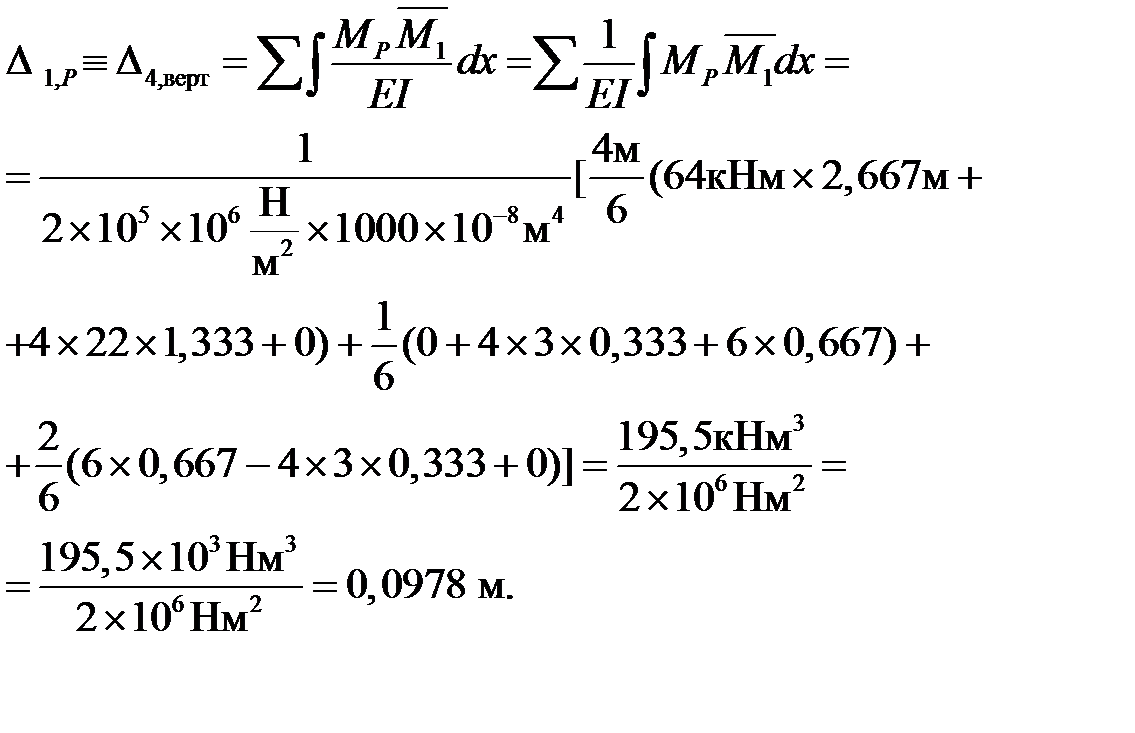
4. Для определения угла поворота сечения 5 прикладываем в этом сечении единичный момент (рис.7.1,з) и строим эпюру изгибающих моментов 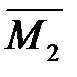 от этого воздействия (рис.7.1,и).
от этого воздействия (рис.7.1,и).
5. По формуле Мора находим угол поворота:
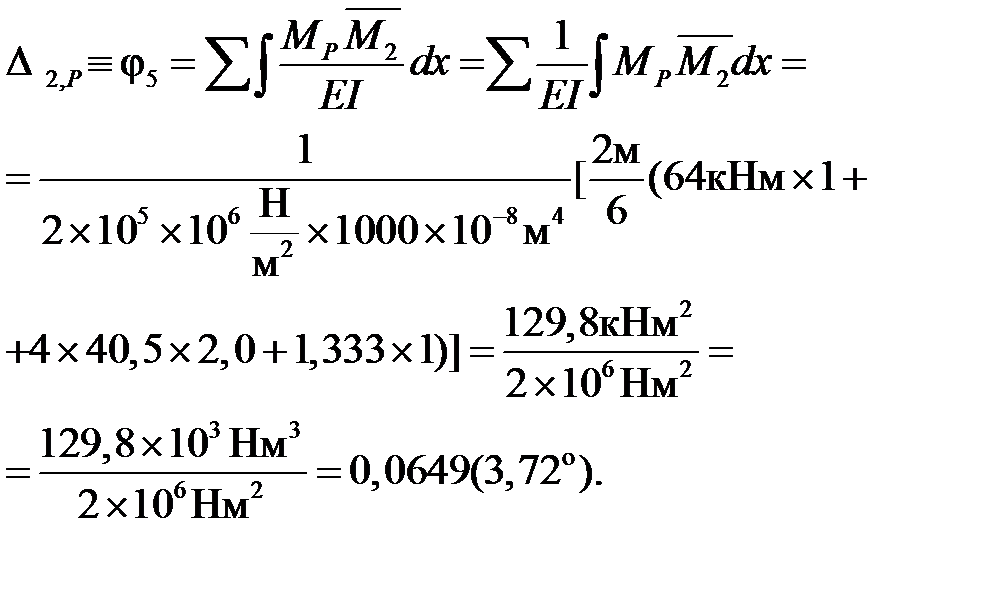
ОБЩАЯ ТЕОРИЯ ЛИНИЙ ВЛИЯНИЯ
В предыдущих разделах курса были рассмотрены методы расчета статически определимых стержневых систем на неподвижную нагрузку. Однако на сооружения может действовать и подвижная нагрузка. Примерами такой нагрузки являются поезд, движущийся по мосту, кран, движущийся по подкрановой балке, и т.п. Расчеты сооружений на подвижную нагрузку имеют следующую особенность — все расчетные величины, которые используются при проектировании, меняются в зависимости от положения движущихся грузов. В связи с этим возникает задача отыскания такого положения подвижной нагрузки, при котором расчетные величины приобретают экстремальные значения. Эту задачу можно решить, перебрав все возможные положения нагрузки и для каждого такого положения проведя расчеты обычным способом. Проанализировав затем результаты расчета, можно найти невыгоднейшее положение нагрузки. Однако такой подход потребует большого объема вычислений. Чтобы избежать этого, в строительной механике разработана теория линий влияния, изучению которой будет посвящено несколько лекций.
В общем случае линией влияния называется график, показывающий изменение какой-либо величины при движении по сооружению единичной силы. Чтобы построить этот график, необходимо установить на сооружение движущийся единичный груз и каким-либо способом получить формулу, описывающую поведение исследуемой величины. Рассмотрим методику построения линий влияния более подробно.
Статическая неопределимость
Как уже отмечалось выше, статически неопределимойназывается такая конструкция, которая содержит лишние с точки зрения обеспечения геометрической неизменяемости связи. Усилия в лишних связях не могут быть найдены из уравнений статики, поэтому приходится составлять дополнительные уравнения, исследуя свойства деформаций системы. Число лишних связей является важной характеристикой рассчитываемой конструкции, поскольку от нее зависит трудоемкость расчета. Эту характеристику называют иначе степенью статической неопределимости. В простейших случаях, когда все лишние связи являются внешними, степень статической неопределимости можно найти как разность между общим числом внешних связей и числом уравнений статики, которые можно составить для конструкции в целом. Например, балка, изображенная на рис.13.1, имеет три лишних связи, поскольку для обеспечения ее неизменяемости достаточно оставить одну неподвижную и одну подвижную опоры. Следовательно, степень статической неопределимости балки равна трем.
Рис.13.1. Статически неопределимая балка
Рис.13.2. Статически неопределимая рама
Рама, изображенная на рис.13.2, дважды статически неопределима, так как количество неизвестных опорных реакций, равное 5, превышает число уравнений статики, равное 3, на 2.
В более сложных случаях, когда стержневая конструкция содержит как внешние, так и внутренние лишние связи, такой простой подсчет степени статической неопределимости невозможен. Для плоских конструкций можно получить, однако, сравнительно простую формулу для определения числа лишних связей.
Рассмотрим П-образную раму с защемленными опорами (рис.13.3).

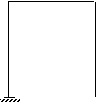
Рис.13.3. П-образная рама Рис.13.4. П-образная рама с
тремя отброшенными связями
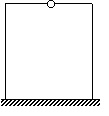

Рис.13.5. П-образная рама Рис.13.6. П-образная рама с
с одним простым шарниром отброшенным шарниром
Очевидно, что рама рис.13.3 трижды статически неопределима; чтобы образовать статически определимую и геометрически неизменяемую конструкцию, необходимо отбросить три связи, как показано, например, на рис.13.4.
Постановка одного простого шарнира, как показано на рис.13.5, снижает степень статической неопределимости на единицу. Действительно, для того, чтобы образовать статически определимую и геометрически неизменяемую конструкцию, из рамы рис.13.5 необходимо отбросить две связи, как показано, например, на рис.13.6.
Таким образом, если рама имеет К замкнутых контуров и содержит Ш простых шарниров, то ее степень статической неопределимости может быть найдена по формуле:
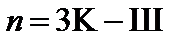 | (13.1) |
Простым шарниромназывается такой узел, в котором шарнирно соединены два элемента. В противном случае шарнир называется кратным. Кратность шарнира равна числу соединяемых элементов, уменьшенному на единицу (см. рис.13.7).
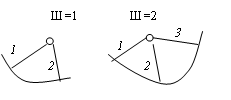
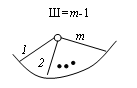
Рис.13.7. К понятию кратности шарнира
Подсчитаем, например, степень статической неопределимости рамы рис.13.2. Рама имеет два замкнутых контура, включая опорный, и четыре простых шарнира, следовательно, n=3×2–4=2. Аналогичный результат был получен выше путем анализа геометрической структуры рамы рис.13.2.
Отметим, что опорные контуры следует включать в число замкнутых контуров в том случае, если они изображаются с помощью шарниров и опорных стержней (рис.13.2). Если же шарнирная опора изображена в виде, показанном на рис.13.8, то опорный контур в этом случае учитывать не надо, а шарнир следует считать простым, так как он соединяет стержень рамы с двумя условными стержнями, образующими жесткое целое с основанием. Шарнир в данном случае соединяет фактически два элемента (стержень рамы и основание), и поэтому является простым.
ЛЕКЦИЯ 14. ПРИМЕРЫ РАСЧЕТА РАМ МЕТОДОМ СИЛ
Таблица 16.1. Эпюры моментов и поперечных сил в однопролетных статически неопределимых балках
| Схема балки и воздействия | Эпюра изгибающих моментов | Эпюра поперечных сил |
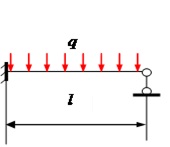 | 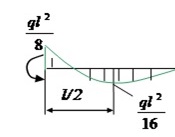 |
|
