Параметры и постоянные времени элементов электропривода

При исследовании динамики ЭП оценивают электромеханические (обусловленные движением вращающихся и поступательно движущихся частей ЭП) и электромагнитные процессы, протекающие в системе и связанные с изменением тока, напряжения, ЭДС и другими параметрами ЭД и преобразователя (П) [2, 4].

Учитывая скоротечность электромагнитных процессов, в первом приближении рассматривают только электромеханические процессы. В тех же случаях, когда необходимо получить более точную модель, следует учитывать и электромагнитные процессы, а для этого нужно знать электрические сопротивления и индуктивности обмоток ЭД и П и соединяющих их цепей. При учете сопротивления соединительных проводов следует иметь в виду увеличение эквивалентного сопротивления за счет коммутационных эффектов в преобразователе, падения напряжения в щеточном контакте и полупроводниковых приборах. Данные о сопротивлении обмоток приводятся в каталогах, причем указывается температура, которой эти данные соответствуют. При необходимости эти сопротивления пересчитываются с учетом нагрузки машины и температуры нагрева обмоток. Экспериментально сопротивление определяют методом амперметра-вольтметра, поскольку при малых сопротивлениях этот метод имеет наибольшую точность. Значительно сложней определить индуктивность обмоток. Дело в том, что электрические обмотки представляют собой цепи со сталью (со стальным сердечником). Кроме того, особенно в машинах переменного тока, одной цепью связано несколько обмоток, поэтому необходимо учитывать не только индуктивности рассеяния, но и взаимные индуктивности, что существенно усложняет расчет.

1.5.1. Электромагнитные процессы[1, 9, 11]

В ЭП, в задачу которых входит регулирование частоты вращения, обычно используются двигатели постоянного тока независимого возбуждения (ДПТ НВ).

В машинах постоянного тока сталь якоря находится в ненасыщенном состоянии, поэтому индуктивность обмоток якоря невелика и часто полагают ее постоянной. Она приводится в некоторых каталогах. В тех случаях, когда этих данных нет, ее можно определить по приближенной формуле Уманского:

, (1.1)

где - частота тока в обмотке якоря;

- коэффициент пропорциональности; и для машин без компенсации , а для машин с компенсацией .

Экспериментально индуктивность обмотки якоря находят по кривой гашения тока (рис.1.2,б). Для этого собирается следующая схема (рис.1.2,а):

а)

б)

Рис.1.2. Схема для определения изменения тока (а), кривая гашения тока (б)

Якорь машины при неподвижной машине подключается через сопротивление к сети постоянного тока и спустя некоторое время замыкается накоротко ключом . При этом осциллограф, N включенный в цепь якоря, фиксирует кривую изменения тока во времени.

Очевидно, что эта кривая описывается уравнением первого порядка: ,

из которого можно определить постоянную времени

. (1.2)

То есть постоянная времени цепи якоря может быть найдена исходя из значения тока и его производной в любой точке кривой. Графически можно найти как подкасательную для любой точки кривой гашения тока. Учитывая некоторое насыщение железа, находят усредненное значение .

Индуктивность обмоток возбуждения является функцией тока возбуждения (рис.1.3) и изменяется в зависимости от насыщения в несколько раз. Для нахождения индуктивности обмоток возбуждения пользуются кривой намагничивания или характеристикой холостого хода машины, при этом расчет производят по усредненной характеристике, без учета гистерезиса. Для всей обмотки возбуждения, расположенной на двух полюсах, индуктивность находится так:

, (1.3)

где - число полюсов;

- число витков обмотки на одном полюсе;

- магнитный поток, пронизывающий полюс, причем ;

- магнитный поток, который проходит через зазор в якорь;

- поток рассеяния;

- ток возбуждения.

L

Рис.1.3. Характер изменения индуктивности (L) при изменении тока возбуждения ( )

Для машин последовательного возбуждения расчеты проводятся аналогично. Для машин смешанного возбуждения необходимо еще экспериментально определить взаимную индуктивность обмоток возбуждения, которая существенно сказывается в переходных режимах. При расчетах обычно оперируют с магнитодвижущими силами, суммируя соответствующие магнитные потоки.

В приводах переменного тока электромагнитные явления часто не учитываются. Если же их учет необходим, то необходимо использовать электромагнитные параметры обмоток, которые приводятся в некоторых каталогах или заводских формулярах. Их экспериментальное определение требует большого объема исследований.

1.5.2. Электромеханические процессы [1]

Среди механических параметров наибольшее значение для динамики имеет момент инерции вращающихся частей. Моментом инерции тела относительно оси, проходящей через центр тяжести, называется сумма произведений масс элементарных частиц на квадрат расстояния их до этой оси: . В практических расчетах обычно используют . При этом радиусом инерции называется расстояние от оси вращения (проходящей через центр тяжести), на котором надо поместить массу рассматриваемого тела, сосредоточенную в одной точке, чтобы удовлетворялось равенство: .

В большинстве ЭП основная часть момента инерции приходится на долю ротора или якоря двигателя ( ), то есть в первом приближении можно считать, что момент инерции привода примерно равен моменту инерции двигателя. При этом следует иметь в виду, что целый ряд механизмов обладает большими моментами инерции, не учитывать которые нельзя даже в первом приближении. Для более точного расчета переходных процессов необходимо определить моменты инерции рабочей машины и, приводя их к валу ЭД, определить момент инерции всего привода. Если моменты инерции двигателя даются в каталогах, то моменты инерции рабочей машины приходится рассчитывать или определять экспериментально. Для этого часто используют метод выбега.

Момент инерции входит как один из основных параметров при определении электромеханической постоянной времени . Рассмотрим этот процесс.

Момент ЭД при линейной механической характеристике может быть представлен:

, (1.4)

где - момент короткого замыкания, пропорциональный приложенному напряжению;

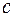- крутизна механической характеристики;

w - угловая скорость ротора.

Уравнение движения одномассовой системы может быть записано так:

. (1.5)

Подставим уравнение момента ЭД в уравнение движения, получим:

=> => .

Поделим на с:

=> ,

где - электромеханическая постоянная времени;

- передаточный коэффициент по входному воздействию;

- передаточный коэффициент по возмущающему воздействию.

Учитывая сказанное, в первом приближении электромагнитными процессами пренебрегают и рассматривают ЭП как механическую систему. Такой подход используется часто при анализе приводов переменного тока. Это обусловлено отчасти еще и тем, что описать электромагнитные процессы в приводах переменного тока очень сложно.

1.6. Структурные схемы и передаточные функции элементов электропривода [1, 9]

Поскольку основным элементом ЭП является электрический двигатель, рассмотрим структурную схему и определим передаточную функцию (ПФ) двигателя постоянного тока независимого возбуждения (так как он нашел наибольшее распространение в системах управления).

Будем считать, что , то есть двигатель управляется только по цепи якоря.

При выводе уравнения, описывающего ЭД, пользуются уравнением ЭДС двигателя:

(1.6)

и уравнением движения:

. (1.7)

Первое описывает электромагнитные процессы, а второе - электромеханические. Для удобства уравнения (1.6 и 1.7) запишем в виде:

(1.8)   (1.9)

где I_с – ток, соответствующий нагрузке M_с, а

.

Рассматривая уравнение ЭДС, получим:

, (1.10)

где - электромагнитная постоянная времени цепи якоря.

Если на входе звена мы имеем разность напряжения и ЭДС, то на выходе получим падение напряжения на якоре. Следовательно, уравнение (1.6) можно представить апериодическим звеном.

Умножим уравнение (1.9) на :

. (1.11)

А так как , то, выразив отсюда и подставив в уравнение (1.11), получим:

. (1.12)

Обозначим - электромеханическая постоянная времени.

Из уравнения (1.12) получим:

(1.13)

где - коэффициент, определяемый током статической нагрузки.

Если на входе звена есть разность падения напряжения на якоре от I и от I_С, то на выходе звена получим E, т.о. уравнению (1.13) соответствует интегрирующее звено на структурной схеме. Построим структурную схему двигателя (рис.1.4). Эта схема соответствует работе двигателя в системе управления скоростью, и в том числе в системе стабилизации скорости.

Рис.1.4. Структурная схема двигателя при управлении скоростью

При создании следящих систем нас интересует угол поворота выходного вала .

Так как , то , где - коэффициент передачи редуктора.

Структурная схема двигателя для следящего привода будет выглядеть так (рис.1.5):

Рис.1.5. Структурная схема двигателя при управлении углом поворота

В результате ПФ по управляющему воздействию при регулировании скорости может быть записана так:

, (1.14)

где - коэффициент передачи двигателя.

В тех случаях, когда на валу двигателя установлен редуктор и нас интересует ПФ исполнительного механизма, записанная по отношению к выходному валу исполнительного механизма, она будет выглядеть так:

,

где .

В следящей системе ПФ двигателя относительно угла поворота:

(1.15)

На практике часто пользуются упрощенной ПФ ДПТ НВ. Учитывая, что электромагнитные процессы протекают значительно быстрее электромеханических, , ими пренебрегают и тогда ПФ двигателя:

, (1.16)

а для следящей системы: . (1.17)

В некоторых случаях для облегчения процедуры синтеза регулятора в системах с подчиненным регулированием координат ПФ двигателя упрощают, пренебрегая ОС по ЭДС. В результате

. (1.18)

Для получения ПФ двигателя по моменту, составим соответствующую структурную схему:

Рис.1.6. Структурная схема двигателя по возмущающему воздействию

ПФ двигателя по моменту:

, (1.19)

где - коэффициент передачи двигателя.

Теперь рассмотрим асинхронный двигатель.

В машинах переменного тока переходные процессы описываются системой уравнений, в которую входят постоянные времени нескольких взаимосвязанных цепей, поэтому исследование электромагнитных процессов представляет очень сложную задачу. На практике сегодня электромагнитные процессы в машинах переменного тока исследуются обычно в режиме установившейся скорости, что для большинства приводов нехарактерно, поэтому в процессе расчета ЭП чаще всего электромагнитными процессами пренебрегают, учитывая что они быстротечны и заканчиваются в течение одного периода изменения напряжения.

Применительно к трехфазному асинхронному двигателю ПФ в системе управления частотой вращения соответствует апериодическому звену первого порядка:

. (1.20)

При этом постоянную времени приходится определять, линеаризуя соответствующий участок характеристики.

Двухфазные АД, используемые в исполнительных механизмах, работают в широком диапазоне скоростей, начиная от пуска и кончая режимом холостого хода (ХХ).

Рис.1.7. Механические характеристики двухфазного исполнительного асинхронного двигателя

При составлении ПФ также пренебрегают электромагнитными процессами, а постоянную времени определяют, используя момент инерции, скорость ХХ и момент КЗ: , то есть для определения постоянной времени возникает необходимость линеаризации механической характеристики, на которой работает двигатель (рис. 1.7). При такой линеаризации постоянная времени двигателя представляет собой условное время разгона до скорости ХХ без статической нагрузки, при условии, что на валу двигателя действует постоянный момент, равный пусковому ( ). Очевидно, что фактическое время разгона Д будет больше за счет уменьшения момента во время разгона, правда снижение момента ограничено в некоторых случаях кривизной характеристики. Сложность состоит еще в том, что при переходе с одной регулировочной характеристики на другую постоянная времени будет меняться, так как меняется крутизна характеристики, определяемая как . Особенно сильно это сказывается при амплитудном управлении. При фазовом управлении изменение постоянной времени будет существенно меньше, поскольку механические характеристики практически параллельны. Другими словами, двухфазный АД, как и трехфазный, описывается апериодическим звеном первого порядка, но в некоторых случаях, особенно при амплитудном регулировании, следует учитывать изменение постоянной времени 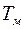.