Задачи с начальными условиями

(Исследование потока нефти на входе насоса при его отключения)

Пример 1. Нестационарное уравнение Навье-Стокса для одномерного потока несжимае­мой жидкости, заданное на интервале длины L, может быть представлено в виде дифференциального уравнения в частных производных (ДУЧП)

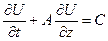
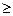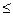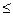заданного при t 0 на интервале 0 z L. Компонентами вектора

U =(р G Т)^Т являются плотность ρ, скорость потока G и температура Т. В вышеприведенной системе ДУЧП используются вектор

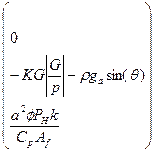и матрица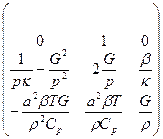

где 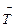= Т+ 273.15. Свойства потока и физические параметры описываются в рабо­те [Thompson & Tuttle, 1986]. В тексте программы ch2ex4.m задаются постоянные значения этих величин, а также определяются другие переменные, идентифика­торы которых соответствуют почти очевидным образом тем обозначениям, кото­рые используются в вышеприведенных уравнениях (например, sinth соответствует sin(θ)). Рассмотрим граничные условия ρ (0,t) = ρ₀ =795.5, T(0,t) = T_о = 255.0, G(L,t) = G₀ = 270.9.

Задача состоит в том, чтобы вычислить стационарное решение этих уравнений. В установившемся режиме выполнено p_t = 0. При этом G(z) является постоянной матрицей G_o на всем интервале 0 < z < L и рассматриваемая система ДУЧП сводится к системе ОДУ

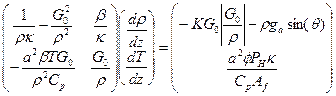
Преобразование системы ДУЧП к системе ОДУ, выполненное в соответствии с вышеприведенной процедурой, позволяет получить решение, которое иногда назы­вают решением для непрерывного пространства и дискретного времени (НПДВ - решение) (continuous space, discrete time solution). В зависимости от граничных условий для исходной системы ДУЧП, этот подход приводит к рассмотрению либо некоторой ЗНУ для системы ОДУ, либо ЗГУ. Система ОДУ может быть проинтегрирована из начального состояния z = 0 в положительном по г направлении до тех пор, по­ка плотность ρ не станет равной плотности насыщения «со стороны жидкости» ρ _sat(T). Можем локализовать это событие с использованием функции обработки события g(z, ρ,T) = ρ (z)- ρ _sat (T(z)).

В чисто иллюстративных целях в программе моделирования используется следу­ющее уравнение состояния ρ _sat (T) = -3.3(Т - 290) + 738.

При вызове ch2ex4.m в MATLAB на экране отображается следующая строка Upper boundary at z = 2.09614 а также график, изображенный на рисунке 12.1. В примере модель стационарного НПДВ-решения используется для исследо­вания потока жидкости на входе насоса при его отключении.

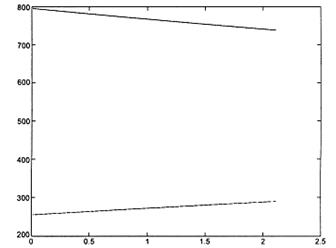Рисунок12.1 - Установившееся решение для верхней границы жидкости

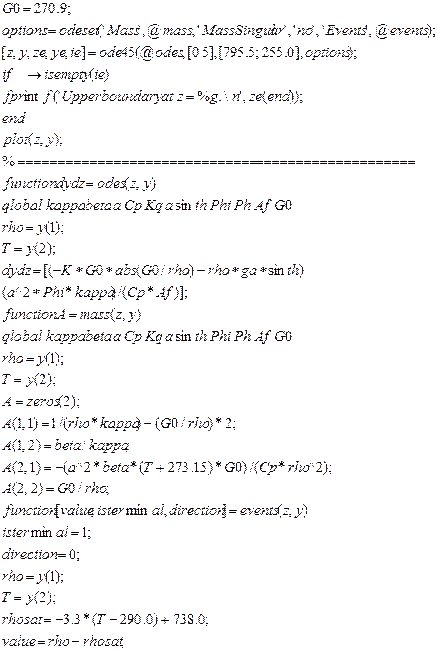
Задание 1.Стандартным применением модели стационарного НПДВ-решения, рассмотренной в примере 1, является исследование процесса экспоненциального убывания по­тока жидкости во входном клапане насоса при его выключении. Найдите НПДВ - решение при 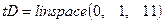, если скорость потока во входном клапане в моменты времени 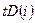определяется равенством 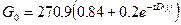. Поставленная задача может быть решена путем модификации программы 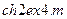, выполненной таким образом, чтобы можно было в цикле получить значения уровня верхней границы 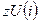жидкости при указанном значении 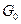. Поскольку в программе 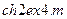уже определена глобальная переменная для скорости потока, необходимо ввести новую переменную в теле цикла перед вызовом 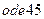. Для графического отображения графика уровня верхней границы как функции от времени используйте команду .

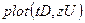Задание 2.Модель термического разложения озона: 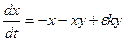, 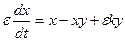где 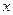– приведенная концентрация озона, 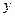- приведенная концентрация кислорода, 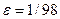и 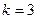- параметры модели. Задача с начальными условиями (ЗНУ) должна быть решена на интервале [0,240] с начальными условиям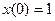и и 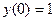. решите эту ЗНУ с использованием 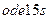и отобразите графически полученное решение 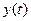с использованием процедур 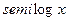и 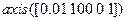. С использованием 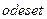установите опцию 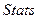в состояние 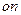. Модель термического разложения озона представлена в форме, которая удобна при применении методов сингулярных возмущений и содержит матрицу весовых коэффициентов 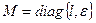. Выполните задание с использованием численных методов интегрирования системы обыкновенных дифференциальных уравнений (ОДУ), представленной в терминах матрицы весовых коэффициентов. При написании программы примите во внимание, что матрица М является постоянной.

Задание 3.В демонстрационной программе 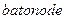в качестве значений длины стержня используется 1, а массы обоих тел — 0.1. Сделайте копию этой программы и мо­дифицируйте ее текст так, чтобы можно было определить движение палочки при новых значениях этих констант: длина L = 2 и масса второго тела m2 равна 0.5. При этом необходимо изменить параметры координатных осей при помощи функции 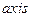. Какие наблюдаются отличия в качественных характеристиках движения палочки при новых значениях констант?

Задание 4.Двойной маятник состоит из двух соединенных между собой простых маятников. Пусть 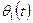и 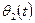— углы отклонения верхнего и нижнего сегментов маятника от вертикальной оси; 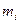— массы, расположенные на концах сегментов; 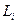— длины сегментов. Если на движение маятника оказывает воздействие только сила гравитации, уравнения движения имеют следующий вид: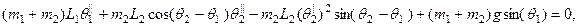

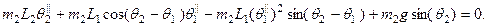
В работе [Giordano & Weir, 1991] рассмотрена модель вертолета Chinook с двумя грузовыми поддонами, подвешенными под вертолетом на стропах. При некоторой идеализации в качестве модели движения этих поддонов можно использовать при­веденную выше модель двойного маятника. При моделировании использовались следующие численные значения: 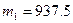и 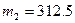слаг¹ — массы верх­него и нижнего поддонов, соответственно; 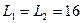футов — длины строп; 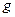— 32 фут/с² — ускорение свободного падения. Крюк, поддерживающий нижний поддон, является не защелкивающимся и поэтому если нижний поддон при коле­баниях отклоняется более чем на 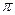/3 радиан, строп может сорваться с крюка и поддон будет потерян. При быстрых маневрах вертолета поддоны приходят в дви­жение, которое может быть промоделировано с использованием представленной модели и при начальных данных

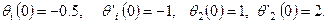
Представленные дифференциальные уравнения могут быть представлены в терми­нах матрицы весовых коэффициентов и непосредственно решены с использованием 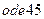при значениях допустимых ошибок вычислений, принятых по умолчанию. Выполните интегрирование на промежутке от t = 0 до t = 2 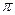, но прекратите вы­числительный процесс, если функция обработки события 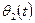— 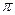/3 обращается в ноль (т.е. если нижний поддон потерян). В указанной работе использовались линеаризованные уравнения

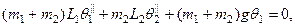
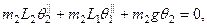
поскольку в этом случае нетрудно найти аналитическое решение. Используемые численные значения параметров удовлетворяют соотношениям g= 2L₁ = 2L₂ и m₁ = 3m₂ и поэтому аналитическое решение имеет простой вид

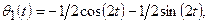
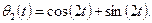
Найдите численное решение представленной линейной модели и сравните полу­ченный результат с аналитическим решением. Кроме того, сравните результаты моделирования линейной и нелинейной модели, обратив особое внимание на зна­чение момента времени, когда нижний поддон срывается с крюка. Результаты этого сравнения должны быть очень близки.