Построение функций принадлежности параметров нечеткому множеству «эксплуатационный объект».

Пример 3.Теория нечетких множеств позволяет работать с категорийными понятиями, такими как «очень плохой», «плохой», «хороший», «очень хороший», которые весьма свойственны человеческому мышлению. Предположим, что понятия «плохой», «посредственный» и «хороший» отображаются на диаграмме нечетких отношений в виде прямой и ломаной. На диаграмме отношений степень предпочтения показывает относительное положение категорийных понятий. Так, например, понятие «плохой» смещено в левую сторону, тогда как понятие «хороший» - в правую сторону. Суть данного подхода заключается в том, что окончательная оценка выделяемого выражается в виде кривой на диаграм­ме, а не в виде числа или порядка отношений.

Построение диаграммы нечетких, «размытых» отношений.

Пример 4.В данной работе впервые предлагается использовать диаграммы нечетких, «размытых» отношений для одной из основных задач РНМ - выделения 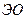. Диаграммы нечетких отношений введены на основе работ Л. Заде (1965). L. Zadehпервый ввел понятие нечеткого множества. Например, нечеткое множество F= {«пористость пласта»} состоит из нечетких элементов {«высо­копористый», «среднепористый», «низко-пористый»}. Элемент «низкопористый» этого нечеткого множества отражается на графике в виде кривой, смещенной в левую сторону.

Задание

1. Описать параметры объекта с помощью лингвистических переменных.

2. Сформировать системы правил ВЭО.

3. Построить диаграммы нечетких, «размытых отношений».

Содержание отчета

1.Титульный лист; 2..Постановка задачи, исходные данные для задания (самостоятельно составить исходные данные для объекта); 3. Введение (краткое описание предметной области и задачи); описанные параметры, объекта СС помощью лингвистических переменных, система правил ВЭО, диаграммы нечетких, «размытых соотношений», Screenshots программной реализации в MATLAB. 4. Выводы по работе.

Практическое занятие №7.

Линейные сети

Цель работы:

- Разработка структурной схемы линейной нейронной сети.

- Разработка алгоритма создания и моделирования линейной нейронной сети.

- Определение параметров созданной нейронной сети.

Теоретические сведения

Линейные сети по структуре аналогичны персептрону и отличаются функцией активации. Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1.

На рисунке 7.1 показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона. Отличается лишь в том, что используется линейная функция активации .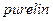

Весовая матрица 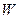имеет одну строку и выход сети определяется следующим выражением:

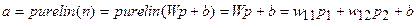. (7.1)

Аналогично персептрону, линейная сеть задается в пространстве входов разделяющую линию, на которой функция активации равна 0 (рис.7.2).

Векторы входа, которые расположены выше этой линии соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. В результате линейная сеть может быть применена для решения задач классификации. Такая классификация может быть выполнена для класса линейно отделимых объектов. Таким образом, линейные сети имеют то же самое ограничение, что и персептрон.

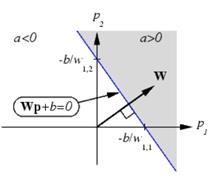Рисунок 7.1	Рисунок 7.2