Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.

Разность множеств А и В обозначают А \ В. Тогда, по оп­ределению, имеем: А \ В = {х \ х Î А и х Ï В].

Если представить множества А и В при помощи кругов Эйлера, то разность А \В изобразится заштрихованной обла­стью.

ПРИМЕРЫ:

Если элементы множеств А и В перечислены и В с А, то, чтобы найти дополнение множества В до множества А, доста­точно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Так, если А = {1,2,3,4,5}, а В = {2, 4}, то В`а = {1,3, 5).

А- это множество четных натуральных чисел В – множество натуральных чисел, кратных 3, то А\В – множество натуральных чисел, не кратных 3.

ДОПОЛНЕНИЕ

Пусть В Ì А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принад­лежат множеству В.

Из определения следует, что В'_а = {х | х Î А и х Ï В}.

ПРИМЕРЫ:

Если элементы множеств А и В перечислены и В с А, то, чтобы найти дополнение множества В до множества А, доста­точно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Так, если А = {1,2,3,4,5}, а В = {2, 4}, то В`а = {1,3, 5).

Так, если А - множе­ство четных чисел, а В - множество чисел, кратных 4, то в'а -это множество, содержащее такие четные числа, которые не делятся на 4. Например, 22 Î в'а , т.к. 22 Î А (т.е. оно четное) и 22 Ï В (т.е. оно не кратно 4).

ПРИМЕРЫ ИЗ НАЧАЛЬНОЙ ШКОЛЫ:

Объединение:

а. У школы посадили 4 липы и 3 березы. Сколько всего деревьев посадили у школы?

б. У Коли было 6 книг. В день рождения ему подарили еще 4 книги. Сколько книг стало у Коли?

Пересечение:

а. У Коли 10 книг, 2 книги он подарил товарищу. Сколько книг осталось у Коли?

В зале было 100 стульев. После того как вынесли несколько стульев, в зале осталось 86 стульев. Сколько стульев вынесли из зала?

3 ВОПРОС:Истомина 1кл.1ч.с.70.

17. Теоретико-множественный смысл отношений "X больше (меньше) Y на а ", заданных на множестве целых неотрицательных чисел. Примеры заданий из начального курса математики, раскрывающих связь данного отношения с операциями над целыми неотрицательными числами.

В аксиоматической теории определение отношения «меньше на» («больше на») естественным образом вытекает из определения отношения «меньше».

Действительно, из того, что а < b тогда и только тогда, когда существует такое натуральное число с, что а + с = b, имеем, что «а меньше b на с» или «b больше а на с».

Итак, с теоретико-множественной точки зрения «а меньше b на с» (или «b больше а на с») означает, что если а = п(А), b = n(B), то в множестве В содержится столько элементов, сколько их в А, и еще с элементов.

Так как с = п(В\В1), где В1Ì В, п(В) = b, п(В1) = а, то, по определению разности, с = а - b.

Следовательно, чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вычесть меньшее.

ПРИМЕРЫ ЗАДАНИЙ ИЗ НАЧАЛЬНОГО КУРСА МАТЕМАТИКИ

Взаимосвязь действий над множествами с действиями над числами, теоретико-множественный смысл отношений «меньше на» и «больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями.

Рассмотрим, например, такую задачу: «На столе 5 чашек, а ложек на 2 больше. Сколько на столе ложек?»

Рассмотрим еще одну задачу: «На столе 5 чашек, а ложек на 2 меньше. Сколько на столе ложек?»

Легко видеть, что она решается при помощи сложения. Почему? В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. п(А) = 5. Число элементов во втором множе­стве требуется найти при условии, что в нем на 2 элемента больше, чем в первом. Отношение «больше на 2» означает, что в множестве В элементов столько же, сколько их в А, и еще 2 элемента. Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, и еще 2. Используя правило подсчета элементов в объединении непересекающихся множеств, получаем: n(B) = n(B1) + n(B\B1) =5+2. Так как 5 + 2 = 7, то получим ответ на вопрос задачи: на столе 7 ложек.

Выясним, почему она решается при помощи вычитания. В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. п(А) - 5. Число элементов во втором множе­стве надо найти при условии, что в нем на 2 элемента меньше, чем в первом. Отношение «меньше на 2» означает, что в множестве В элементов столько же, сколько их в А, но без двух. Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, но без двух. Таким образом, п (В) = п(А1) = п(А)-п(А\А1) =5-2. Так как 5 - 2 = 3. то получим ответ на вопрос задачи: на столе 3 ложки.

3 ВОПРОС:Истомина 1кл.2ч.с.11. Рудницкая 3кл.2ч. с.4

Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Правило установления отношений «равно», «меньше», «больше» для чисел, записанных в этой системе. Примеры заданий из начального курса математики, при выполнении которых младшие школьники знакомятся с особенностями десятичной системы счисления.

Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления.

Называть числа и вести счет людям помогали пальцы рук и ног, верёвочные узлы, зарубки. Но это слишком долго, поэтому счет стали вести группами, состоящими из одинакового числа элементов. Наряду с группами по 10 элементов встречались группы по 5, 12, 20 элементов. В Древнем Вавилоне считали группами по 60 единиц. Древневавилонская система используется до сих пор при измерении времени и углов в минутах и секундах.

Наибольшее распространение получила десятичная система записи чисел. Эта система, принятая сейчас почти всюду, основана на группировании десятками и берет свое начало от счета на пальцах. (Возникла в Индии, первыми её заимствовали арабы).

Различают позиционные и непозиционные системы счисления.

В позиционных системах один и тот же знак может обозначать различные числа в зависимости от места (позиции), занимаемого этим знаком в записи числа. Так, шестидесятеричная вавилонская и десятичная системы счисления являются позиционными.

Непозиционные системы характеризуются тем, что каждый знак (из совокупности знаков, принятых в данной системе для обозначения чисел) всегда обозначает одно и то же число, независимо от места (позиции), занимаемого этим знаком в записи числа. Примером такой системы может служить римская система, возникшая в средние века. В этой системе счисления имеются знаки для узловых чисел:

· единица - I, пять - V,, десять – Х, пятьдесят - L, сто - С, пятьсот- D, тысяча- М.

Все остальные числа получаются при помощи двух арифметических операций: сложения и вычитания. Вычитание производится тогда, когда знак, соответствующий меньшему узловому числу, стоит перед знаком большего узлового числа. Например, IV - четыре, ХС - девяносто.

Запишем несколько чисел в римской нумерации.

193 - это сто (С) плюс девяносто, т.е. сто без десяти (ХС), плюс три (III); следовательно, число 193 записывается как CXCIII.

564 - это пятьсот (D) плюс пятьдесят (L) плюс десять (X) плюс четыре, т.е. пять без одного (IV). Следовательно, 564 записывается как DLXIV.

2708 - это две тысячи (ММ) плюс пятьсот (D) плюс сто (С) плюс сто (С) плюс пять (V) плюс три (III). Следовательно, число 2708 записывается так: MMDCCVIII.

Если число содержит несколько (немного) тысяч, то для его записи в римской нумерации пользуются повторением знака М. Вообще же числа четырех-, пяти- и шестизначные записывались с помощью буквы m (от лат. слова mille - тысяча), слева от которой записывали тысячи, а справа - сотни, десятки, единицы. Так, запись CXXXIIImDCCCXLII является записью числа 133842.

Римская система записи чисел была удобнее, чем зарубки на бирках, поскольку позволяли записывать большие числа. Однако выполнение действий над ними было весьма сложным делом. Поэтому на смену им пришла десятичная система счисления.

Правило установления отношений «равно», «меньше», «больше» для чисел, записанных в десятичной системе счисления.

Чтобы установить отношения «равно», «меньше», «больше»для чисел, записанных в десятичной системе счисления, необходимо определить разрядность данных чисел (если отличается, то больше то число, в котором больше разрядов). Если количество разрядов в числах совпадает, то сравнение начинается со старшего разряда.

3 ВОПРОС:Истомина 1кл.2ч.с.31. Рудницкая 3кл.1ч. с.46

Алгоритм сложения многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в их основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данного алгоритма.

В начальной школе эти алгоритмы известны под: сложением, вычитание, умножением, делением многозначных чисел в столбик.

В основе алгоритмов письменного сложения и вычитания лежат следующие теоретические положения:

1. Представление числа в десятичной системе счисления.

6145 = 6*10³ + 1*10² + 4*10 + 5

Представление числа в десятичной системе счисления аналогом в начальной школе является разрядный состав числа.

2. Предлагая учащимся записать одно слагаемое под другим, а также вычитаемое, разряд под разрядом, мы тем самым раскрываем такие теоретические основы данных алгоритмов, как коммутативно-ассоциативное свойство сложения, а также правило вычитания числа из суммы и суммы из числа.

3. В основе сложения и вычитания многозначных чисел также лежит дистрибутивный закон умножения относительно сложения и вычитания соответственно.

4. Общее положение лежащее в основе данных письменных вычислительных алгоритмов – табличные случаи сложения однозначных чисел.

451 + 237 (представление чисел в десятичной системе счисления) ===

=== (4*10² + 5*10 + 1) + (2*10² + 3*10 + 7) (ассоциативный и коммутативный законы) === (4*10² + 2*10²) + (5*10 + 3*10) + (1+7) (дистрибутивный закон умножения относительно сложения) === (4+2)*10² + (5+3)*10 + (1+7) (табличное сложение) === 6*10² + 8*10 + 8 (представление числа в десятичной системе счисления) === 688.

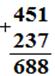
Для того, чтобы упростить указанную запись, представим эту запись "в столбик".

Алгоритм письменного сложения многозначных чисел:

1. Записываем второе слагаемое под первым строго разряд под разрядом.

2. Сложение начинаем с разряда единиц: число единиц второго слагаемого прибавляем к числу единиц первого слагаемого.

Если полученный результат < 10, записываем его в разряд единиц суммы и переходим к сложению в следующем разряде.

Если полученный результат >= 10, то представляем его в виде 10 + c, где с – однозначное число. С записываем в разряд единиц суммы, увеличивая одновременно число единиц в разряде первого десятка на 1.

3. Повторяем один из процессов.

4. Сложение считаем законченным после того, как сложены единицы старших разрядов.

3 ВОПРОС:Рудницкая 3кл.1ч. с.46

Алгоритм умножения многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в его основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данного алгоритма.

Кроме алгоритмов письменного сложения и вычитания, изучаемых в курсе математики в начальной школе, также изучается алгоритм письменного умножения многозначных чисел в десятичной системе счисления.

Алгоритм письменного умножения многозначных чисел подразделяется на следующие этапы:

1. умножение многозначного числа на однозначное

2. умножение многозначного числа на степень числа 10

3. сложение многозначных чисел

В основе алгоритма письменного умножения многозначного числа на однозначное лежат следующие положения:

- представление числа в десятичной системе счисления

- свойство действий умножения и деления

- табличное умножение однозначных чисел

Рассмотрим указанные теоретические положения на конкретном примере: 231* 3 (представление числа в десятичной системе счисления) = (2 * 10² + 3 * 10¹ + 1) * 3 (дистрибутивный закон умножения относительно сложения) = (2 * 10²) * 3 + (3 * 10) * 3 + 1 * 3 (коммутативный и ассоциативный законы умножения) = (2 * 3) * 10² + (3 * 3) * 10 + 1 * 3 (табличное умножение однозначных чисел) = 6 * 102 + 9 * 10 + 3 (представление числа в десятичной системе счисления) = 693.

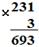Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного умножения многозначного числа на однозначное, предлагается представить эту запись в следующем виде, называя его письменным умножением многозначного числа на однозначное в столбик.

Алгоритм письменного умножения многозначного числа на однозначное:

1. Второй множитель записываем под первым.

2. Умножение начинаем с разряда единиц: число единиц разряда единиц первого множителя умножаем на второй множитель.

Если полученный результат < 10, записываем его в разряд единиц произведения.

Если полученный результат >= 10, то представляем его в виде 10 * q + c, где с – однозначное число. С записываем в разряд единиц произведения, а q запоминаем.

3. Переходим к умножению в следующем разряде; если необходимо полученный результат увеличиваем на q и повторяем один из записанных процессов.

4. Умножение считаем законченным, если умножили на однозначное число единицы старшего разряда первого множителя.

Умножение числа на степень числа 10, как известно, сводится к тому, что к десятичной записи числа приписывается справа столько нулей, сколько указано показателей степени числа 10.

Если мы будем рассматривать умножение числа на число у * 10^k, где у – однозначное число (300 = 3*10²), то сначала многозначное число умножается на однозначное у, а затем справа к полученному произведению приписывается столько нулей, сколько соответствует показателю k.

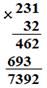Разберем на конкретном примере умножение в столбик трехзначного числа на двузначное:

Сначала умножаем число 231 на 2 и получаем 462. Далее мы умножаем 231 на 30. Для этого 231 мы сначала умножаем на 3, а затем к полученному числу прибавляем справа 0. Полученное произведение записываем под первым произведением, смещая его на один разряд влево. Это смещение подразумевает факт умножения числа на степень числа 10. Полученные числа 462 и 693 называют неполными произведениями. Потом эти числа складываются по правилу сложения многозначных чисел в столбик, и получается ответ. *Во втором неполном произведении можно было записать цифру 0, но т.к. при прибавлении 0 к любому числу значение числа не меняется, то принято этот 0 не писать, но если учитель чувствует, что эта подсказка имеет значение, то можно его записать.

При письменных вычислительных приемах выполнение действия начинается с наименьших разрядов, а при устных со старших разрядов.

3 ВОПРОС:Истомина 3-4кл.
21. Определения отрезка, луча, угла, ломаной линии. Основные свойства этих фигур. Содержание данных понятий в начальном курсе обучения математике; виды определений. Примеры заданий из учебника математики для начальной школы, раскрывающих объём и содержание понятия угла.

При ознакомлении учащихся начальной школы с различными геометрическими понятиями основной упор делается на те знания учащихся о геометрических понятиях, которые они почерпнули из практической своей деятельности.

Пример: при письме ребёнку предлагается выполнить упражнение: поставить точку, обвести квадратик, соедини нижнюю и верхнюю вершины клетки.

Одно из первых геометрических понятий, с которым знакомятся учащиеся, является точка. Учащимся предлагается поставить две точки на некотором расстоянии друг от друга и соединить эти точки по прямой. В результате появляется геометрическая фигура на плоскость, которая называется отрезком.

Отрезок – это множество точек плоскости лежащих на одной прямой и ограниченных с двух сторон.

Например:

-Между двумя точками этого отрезка существует бесконечное число точек этого отрезка.

- А точки, ограничивающие этот отрезок, являются его концами.

- Концы отрезка обозначаются заглавными латинскими буквами, и тем самым отрезку даётся имя.

Угол - это геометрическая фигура образованная двумя лучами, исходящими из 1 точки, эта точка называется вершиной угла, а лучи его сторонами. На письме угол обозначается с помощью специального знака.

Различают понятие «угла» и «плоского угла». Под углом понимается понятие луча исходящего из одной точки. Под плоским углом - часть плоскости ограниченной двумя лучами, исходящими из 1 точки.

Развёрнутым углом называется угол, у которого стороны лежат на одной прямой (радианная мера = 180°).

Прямой угол – половина развёрнутого угла и его радианная мера = 90°.

Острый угол –определяется как,угол, который меньше прямого угла, т.е. меньше 90°.

И с понятием тупого угла - угол больше прямого угла, т.е. больше 90°.

· При изучении понятия «угла», дети должны распознавать объекты принадлежащие объёму такого понятия как «угол».

· Должны научиться с помощью линейки выполнять простейшее построение угла.

· Важно учить детей обосновывать свои умозаключения при определении вида того или иного угла.

Особо интересны и важны для детей задания, в которых им предлагается найти углы в различных геометрических фигурах, а так же в предметах и объектах окружающих ребёнка.

Луч -это часть прямой ограниченной с одной стороны.

С понятием луча связано понятие «числовой луч», которое используется при изучении различных математических понятий, а также определённых вычислительных приёмов.

Ломаная линия – совокупность отрезков, у которых каждый конец отрезка является началом следующего.

Ломаные линии бывают:

1.Замкнутые – когда начало первого отрезка совпадает с концом последнего.

2. Если ломаная линия не имеет самопересечения, то она называется - простой.

3. Имеющая самопересечения, т. е. не является простой.

Пример: среди множества объектов, которые являются различными линиями им нужно найти ту линию, которая является прямой. (строить эту линию нужно при помощи линейки) У этой лини нет ни конца, ни края – эта линия прямая.

Изучение геометрических понятий проходит достаточно продуктивно и системно уже с первых дней обучения ребёнка в школе. Истомина Наталья Борисовна предлагает изображать различные геометрические фигуры как: отрезок, точка, ломанная, предлагая учащимся рисовать различные бордюры (орнаменты).

3 ВОПРОС:Истомина 2кл.1ч.с.56. Моро 2кл.2ч.с24 Рудницкая 3кл.2ч. с.24

22. Различные определения понятия «прямоугольник». Свойства прямоугольника. Определение понятия «прямоугольник» в начальном курсе обучения математике и алгоритм его использования при распознавании прямоугольников.

Прямоугольник– это один из видов геометрических фигур, который подробно изучается в курсе математики в начальной школе.

Если говорить о других геометрических фигурах, таких как угол, отрезок, треугольник, круг, то объем содержания, который рассматривается в начальной школе, достаточно узок. В случае же с прямоугольником, объем, раскрываемых существенных свойств этого понятия значительно более широк.

Учащиеся знакомятся с целым рядом существенных свойств указанного понятия, а именно, что у квадрата:

- противоположные стороны равны

- все углы равны 90 градусам - прямые

- чему равны периметр и площадь прямоугольника

- что прямоугольник – вид четырехугольника

Т.к. прямоугольник – это видовое понятие по отношению к понятиям , «параллелограмм», «четырехугольник», то соответственно прямоугольнику можно давать различные определения в зависимости от родового понятия.

Прямоугольник – это параллелограмм, у которого все углы прямые

Прямоугольник – это четырехугольник , у которого все углы прямые

Признаки прямоугольника:

1. Если в четырехугольнике противоположные стороны равны и каждый угол равен 90⁰, то этот четырехугольник – прямоугольник.

2. 4 вершины, 4 стороны, 4 угла, все углы прямые.

3. Квадрат -прямоугольник

Т.к. – это и четырехугольник и параллелограмм, то он обладает всеми теми свойствами, которые присущи как параллелограмму, так и четырехугольника.