Изучение основных операций над нечеткими множествами
Цель работы:изучить понятие нечеткого множества и основные операций над нечеткими множествами.
Теоретические сведения
Значительный шаг в направлении развития теории нечетких множеств (ТНМ) сделал профессор Калифорнийского университета Лотфи А. Заде (1965 г. - публикация работы “ 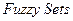 ”). Заде расширил понятие множества, допустил, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0, 1]. Такие множества были названы им нечеткими (
”). Заде расширил понятие множества, допустил, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0, 1]. Такие множества были названы им нечеткими ( 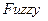 ).
).
Пусть Е – универсальное множество, х – элемент Е, Р – некоторое свойство. Обычное (четкое) множество А универсального множества Е, элементы которого удовлетворяют свойству Р, определяются как множество упорядоченных пар 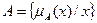 , где
, где 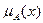 - характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
- характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
В ТНМ для элементов х из Е нет однозначного ответа «да/нет» относительно свойства Р. В связи с этим нечеткое множество А универсального множества Е определяется как множество упорядоченных пар с функцией принадлежности 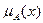 , принимающей значение в некотором упорядоченном множестве М (например, М=[0, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0, 1},то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
, принимающей значение в некотором упорядоченном множестве М (например, М=[0, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0, 1},то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
Основные операции над нечеткими множествами:
Включение.Пусть А и В нечеткие множества на универсальном множестве Е. А содержится в В, если 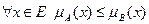 . Обозначается А
. Обозначается А 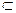 В.
В.
Равенство.А и В равны, если 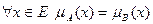 . Обозначение: А=В.
. Обозначение: А=В.
Дополнение.Пусть М=[0,1], А и В дополняют друг друга, если 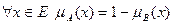 . Обозначается В=
. Обозначается В= 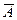 или
или 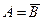 .
.
Пересечение. 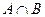 - наименьшее нечеткое подмножество, содержащееся одновременно в А и В:
- наименьшее нечеткое подмножество, содержащееся одновременно в А и В: 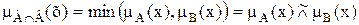 .
.
Или, по другому, определение в классе треугольных норм (t – норма).
Типичными t - нормами являются [2, 3]:
- операция min как нечеткое логическое произведение с нечеткими переменными Х1, Х2: 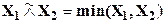 ;
;
- алгебраическое произведение 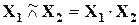 .
.
Объединение. 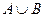 - наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
- наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
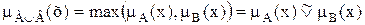 .
.
Или, по другому, определение в классе треугольных конорм (s – норма).
Типичными s - нормами являются:
- операция нечеткого логического сложения 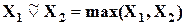 ;
;
- алгебраическая сумма 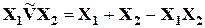 ,
,
где «~» означает нечеткую логическую операцию.
Разность.А-В= 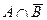 с функцией принадлежности:
с функцией принадлежности: 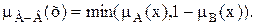
Нечеткие отношения.Нечеткое n-мерное отношение определяется как нечеткое подмножество R на Е, принимающее свои значения в М. В случае n=2 и М=[0,1] нечетким отношением R между множествами Х=Е1 и Y=Е2 будет называться функция R: (X, Y) → [0,1], которая ставит в соответствие каждой паре элементов (x,y) 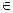 X x Y величину
X x Y величину 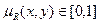 .
.
Обозначение: 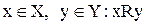 .
.
Алгебраические операции над нечеткими отношениями аналогичны операциям с нечетким множествам.
Композиция (свертка) двух нечетких отношений.Пусть R1 – нечеткое отношение R1: (X x Y) →[0,1] между X и Y, и R2 – нечеткое отношение R2: (Y x Z) →[0,1] между Y и Z. Нечеткое отношение между X и Z обозначается R1●R2 и определяется как
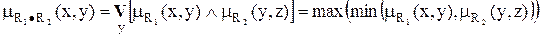 , где символ
, где символ 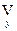 - обозначает операцию выбора наибольшего по y значения и называется (max-min)-сверткой отношений R1 и R2.
- обозначает операцию выбора наибольшего по y значения и называется (max-min)-сверткой отношений R1 и R2.
Пример 1.
1Пусть Е ={x1, x2, x3, x4, x5}; А – нечеткое множество, для которого  =0,3;
=0,3;  =0;
=0; 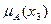 =1;
=1; 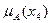 =0,6;
=0,6; 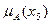 =0,9.
=0,9.
Тогда А можно представить в виде
А = {0,3/x1; 0/x2; 1/x3; 0,6/x4; 0,9/x5}.
Пример 2.
Пусть заданы отношения R1 и R2.
Таблица 1.1
| R1 | y1 | y2 | y3 |
| x1 | 0,1 | 0,7 | 0,4 |
| x2 | 0,5 |
Таблица 1.2
| R2 | z1 | z2 | z3 | z4 |
| y1 | 0,9 | 0,2 | ||
| y2 | 0,3 | 0,6 | 0,9 | |
| y3 | 0,1 | 0,5 |
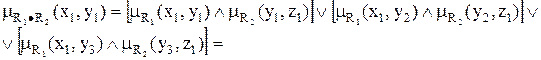
= (0,1 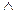 0,9)
0,9) 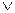 (0,7
(0,7 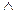 0,3)
0,3) 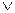 (0,4
(0,4 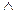 0,1)=0,1
0,1)=0,1 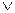 0,3
0,3 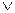 0,1=0,3.
0,1=0,3.
Таблица 1.3
| R1· R2 | z1 | z2 | z3 | z4 |
| х1 | 0,3 | 0,6 | 0,1 | |
| х2 | 0,9 | 0,5 |
Пример 3. Пусть на универсальном множестве E заданы нечеткие множества A, B, C:
A= {1/x1; 0/x2; 0/x3; 0.1/x4},
B= {1/x1; 0/x2; 0.1/x3; 0.2/x4},
C= {1/x1; 0.2/x2; 0.1/x3; 0.8/x4}.
Определим, выполняются ли условия:
1) 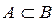 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 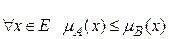 .
.
2) 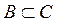 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 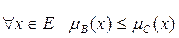 .
.
3) 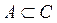 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 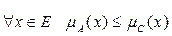 .
.
4) 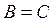 – равенство. Данное условие не выполняется, так как не выполняется условие
– равенство. Данное условие не выполняется, так как не выполняется условие 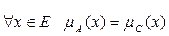 .
.
5) 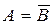 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 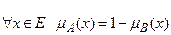 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
6) 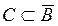 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 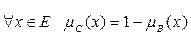 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
7) 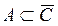 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 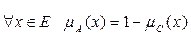 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
Рассчитаем:
1) 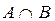 – пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B, функция принадлежности для которого рассчитывается по формуле:
– пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B, функция принадлежности для которого рассчитывается по формуле: 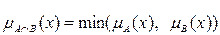 .
.
Тогда получаем 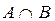 ={1/x1; 0/x2; 0/x3; 0.1/x4}.
={1/x1; 0/x2; 0/x3; 0.1/x4}.
2) 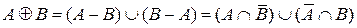 с функцией принадлежности:
с функцией принадлежности: 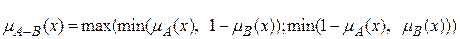 .
.
Тогда получаем 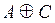 ={0/x1; 0/x2; 0.1/x3; 0.1/x4}.
={0/x1; 0/x2; 0.1/x3; 0.1/x4}.
3) 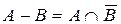 с функцией принадлежности:
с функцией принадлежности:
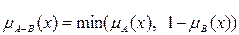 .
.
Тогда получаем  ={0/x1; 0/x2; 0/x3; 0.1/x4}.
={0/x1; 0/x2; 0/x3; 0.1/x4}.
4) 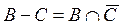 с функцией принадлежности:
с функцией принадлежности:
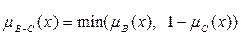 .
.
Тогда получаем 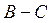 ={0/x1; 0/x2; 0.1/x3; 0.2/x4}.
={0/x1; 0/x2; 0.1/x3; 0.2/x4}.
Заданияпредставлены в приложении 1 для решения основных операций над множествами.
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Для решения основных операций над множествами решить задания представленные в приложение 1.
3. Подготовить отчет о работе с краткими теоретическими сведениями и примерами и с представлением и объяснением полученных результатов.
Практическое занятие № 2
Построение нечеткой аппроксимирующей функции у=х2
Цель работы:изучить создание системы нечеткого вывода для аппроксимации функции.
Теоретические сведения
В экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:
П1: если х есть А1, то y есть В1,
П2: если х есть А2,то y есть В2,
…
Пn: если х есть Аn,то y есть Вn,
где х – входная переменная, y – переменная вывода, А и В – функции принадлежности, определенные на х и y соответственно.
Знания эксперта А→В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его называют нечетким отношением:
R= А→В, где «→» - нечеткая импликация.
Отношение R можно рассматривать как нечеткое подмножество прямого произведения Х ´ Y полного множества предпосылок X и заключений Y. Таким образом, процесс получения (нечеткого) результата вывода В′ с использованием данного наблюдения А′ и значения А→В можно представить в виде В′= А′● R= А′●( А→В).
Алгоритм нечеткого вывода:
1 Нечеткость (фаззификация, fuzzification). Функции принадлежности, определенные для входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила).
2 Логический вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено переменной вывода для каждого правила. В качестве правил логического вывода используются только операции min (минимума) или prod (умножение).
3 Композиция. Нечеткие подмножества, назначенные для каждой переменной вывода (во всех правилах), объединяются вместе, чтобы сформировать одно нечеткое подмножество для каждой переменной вывода. При подобном объединении обычно используются операции max (максимум) или sum (сумма).
4 Дефаззификация – приведение к четкости (defuzzification). Преобразование нечеткого набора выводов в число.
Алгоритмы нечеткого вывода Сугено (  ) и Такаги (
) и Такаги (  )
)
Сугено (  ) и Такаги (
) и Такаги (  ) использовали набор правил в следующей форме:
) использовали набор правил в следующей форме:
П1: если х есть А1 и y есть В1, тогда z=a1x+b1y,
П2: если х есть А2 и y есть В2, тогда z =a2x+b2y.
1 Первый этап – аналогично алгоритму Мамдани.
2 Определение 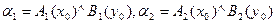 и индивидуальные выходы правил:
и индивидуальные выходы правил: 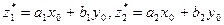 .
.
3 Определяется значение переменной вывода: 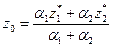 .
.
Представленная форма правил иллюстрирует алгоритм Сугено 1-го порядка. Если правила записаны в форме:
П1: если х есть А1 и y есть В1, тогда z=с1,
П2: если х есть А2 и y есть В2, тогда z =с2,
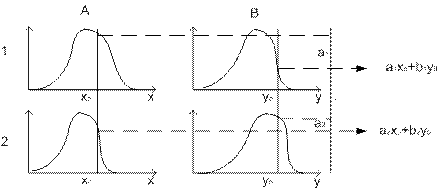
то задан алгоритм Сугено 0-го порядка.
Иллюстрация алгоритма Сугено 0-го порядка представлена на рисунке 1.1.
|
Пример.Построение нечеткой аппроксимирующей функции у=х2.
Исходные данные для аппроксимации представлены в таблице 2.1.
Таблица 2.1
Значения x и y
| X | -1 | -0,6 | 0,4 | ||
| Y | 0,36 | 0,16 |
1 Командой  , из режима командной строки запускается основная интерфейсная программа пакета
, из режима командной строки запускается основная интерфейсная программа пакета  – редактор нечеткой системы вывода.
– редактор нечеткой системы вывода.
2 В меню  выбрать команду
выбрать команду  .
.
3 Выбрать входной элемент системы input1 и ввести в поле  обозначение входной переменной (х).
обозначение входной переменной (х).
4 Войти в режим редактирования функции принадлежности –  (двойное нажатие левой клавиши мыши). Выбором
(двойное нажатие левой клавиши мыши). Выбором  (добавить функцию принадлежности) задать тип функции принадлежности (
(добавить функцию принадлежности) задать тип функции принадлежности ( 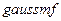 ) и количество (5).
) и количество (5).
5 Установить диапазон (  ) изменения х от -1 до 1 (определяется заданным диапазоном х).
) изменения х от -1 до 1 (определяется заданным диапазоном х).
6 Совместить ординаты максимумов функций принадлежности с значениями аргумента x.
Шаг выполняется двумя способами: выделить редактируемую функцию принадлежности, перетащить мышью кривую функции принадлежности; более точную установку проводят заданием числовых значений параметров функции принадлежности в поле  (первое значение определяет размах кривой, второе – положение центра).
(первое значение определяет размах кривой, второе – положение центра).
В поле  вводится имя функции принадлежности (1- bn, 2 – n, 3 (центральная) – z, 4 – p, 5 – bp).
вводится имя функции принадлежности (1- bn, 2 – n, 3 (центральная) – z, 4 – p, 5 – bp).
Выйти из редактора функций принадлежности –  .
.
7 Ввести в поле название выходной переменной 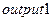 = (y), войти в режим редактирования функций принадлежности.
= (y), войти в режим редактирования функций принадлежности.
8 Задать вид функции принадлежности для выходной переменной. Предлагается выбрать в качестве функции принадлежности линейные (linear) или постоянные ( 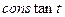 ) – в зависимости от алгоритма Сугено (1-го или 0-го порядка). В поставленной задаче необходимо выбрать постоянные функции принадлежности с общим числом 4 (по числу различающихся значений y). Нажать Ok.
) – в зависимости от алгоритма Сугено (1-го или 0-го порядка). В поставленной задаче необходимо выбрать постоянные функции принадлежности с общим числом 4 (по числу различающихся значений y). Нажать Ok.
9 Установить диапазон ( 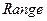 ) – [0, 1]. Изменить значения (
) – [0, 1]. Изменить значения (  ) и задать для выходных переменных имена (
) и задать для выходных переменных имена (  ) соответственно 0; 0,16; 0,36; 1. Закрыть редактор.
) соответственно 0; 0,16; 0,36; 1. Закрыть редактор.
10 Перейти в редактор привил (  ) (дважды щелкнуть на средний белый квадрат разрабатываемой структуры системы нечеткого вывода). При вводе каждого правила необходимо обозначить соответствие между каждой функцией принадлежности аргумента x и числовым значением y. Кривая, обозначенная bn, соответствует y=1, для чего выбирается в левом поле (с заголовком x is) вариант bn, а в правом – 1 и нажимается кнопка
) (дважды щелкнуть на средний белый квадрат разрабатываемой структуры системы нечеткого вывода). При вводе каждого правила необходимо обозначить соответствие между каждой функцией принадлежности аргумента x и числовым значением y. Кривая, обозначенная bn, соответствует y=1, для чего выбирается в левом поле (с заголовком x is) вариант bn, а в правом – 1 и нажимается кнопка  . Введенное правило появится в окне правил в виде
. Введенное правило появится в окне правил в виде 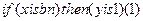 .
.
Аналогично вводятся все правила (всего 5). Закрыть окно редактора правил и вернуться в окно FIS-редактора. Построение системы закончено.
Сохранить на диске (  ) созданную систему. Перейти в редактор функций принадлежности (
) созданную систему. Перейти в редактор функций принадлежности (  ). Из окна редактора командой можно перейти в окно просмотра правил (
). Из окна редактора командой можно перейти в окно просмотра правил (  ), просмотра поверхности (
), просмотра поверхности (  ).
).
В окне просмотра правил иллюстрируется процесс принятия решения (вычисления y). Красная вертикальная черта, пересекающая графики в правой части окна, которую можно перемещать с помощью мыши, позволяет изменять значения переменной входа (либо вводят значение с клавиатуры в поле Input), при этом соответственно изменяется значение выхода.
Просмотр кривой y(x) осуществляется командой  . Большая погрешность аппроксимации заданной зависимости объясняется малым числом экспериментов.
. Большая погрешность аппроксимации заданной зависимости объясняется малым числом экспериментов.
С помощью рассмотренных редакторов на любом этапе проектирования нечеткой модели можно внести необходимые коррективы, например задание пользовательской функции принадлежности.
В рассмотренном примере использованы следующие операции, устанавливаемые по умолчанию в алгоритме Сугено:
- логический вывод организуется с помощью операции логического умножения (prod);
- композиция организуется с помощью операции логической суммы (вероятностного ИЛИ, probor);
- приведение к четкости (дефаззификация) организуется дискретным вариантом центроидного метода (взвешенным средним, wtaver).
Задание.Создать систему нечеткого вывода для аппроксимации функции y=k*x2 (вариант см. в таблице 2.2). Для аппроксимации взять 10 значений функции.
Таблица 2.2 – Варианты задания для аппроксимации функции
| Вариант | ||||||||||
| k | 1.5 | 1.8 | 1.3 | 1.9 | 2.2 | 1.4 | 2.5 | 2.3 | 2.4 | |
| mf input | trimf | gaussmf | trimf | gaussmf | trimf | trimf | trimf | gaussmf2 | trimf | gaussmf |
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Согласно варианту задания для аппроксимации функции создать систему нечеткого вывода.
3. Подготовить отчет о работе с краткими теоретическими сведениями и примерами, с представлением и объяснением полученных результатов, графиков, вывод.
Практическое занятие № 3
