Выбор типа и параметров тяговой передачи

Выбор и обоснование типа привода проводится на основании анализа данных приведенных в п.4.1. и их сопоставления с требованиями, которые предъявляются к локомотиву определенного рода службы.

Последовательность расчета основных параметров тяговой передачи – передаточного отношения, диаметров зубчатых колес, числа зубьев, межосевого расстояния удобно рассмотреть на примере привода первого класса, а затем указать на ряд различий при определении этих величин для приводов второго и третьего классов.

5.2.1. Привод первого класса

Одним из основных параметров тяговой передачи, который непосредственно влияет на тяговые свойства локомотива, является передаточное отношение тягового редуктора. Передаточным отношением называется отношение числа зубьев зубчатого колеса к числу зубьев шестерни.

Предварительно передаточное отношение 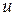определяется после выбора тягового двигателя и диаметра колес. Оно находится из условия обеспечения заданной (расчетной) скорости локомотива на расчетном подъеме по формуле

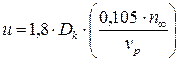; (5.1)

где 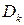– диаметр колес локомотива, м; 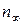– частота вращения тягового двигателя в продолжительном режиме, об/мин; 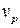– расчетная скорость локомотива, км/ч.

Полученное передаточное отношение должно позволять локомотиву достигнуть конструкционной скорости при максимальной скорости вращения тягового двигателя. Таким образом, должно выполняться условие:

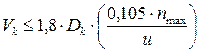; (5.2)

где 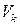– конструкционная скорость локомотива, км/ч; 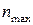– максимальная частота вращения тягового двигателя, об/мин.

Выбор и расчет основных параметров тягового редуктора производится исходя из определения максимального возможного значения передаточного отношения.

Тяговый двигатель и элементы тяговой передачи размещаются в монтажном объеме, который ограничен в вертикальном направлении расстоянием от головки рельса до необрессоренных и обрессоренных элементов тягового привода, т.е. клиренсом, а в поперечном направлении – расстоянием между колесами. Таким образом, величина передаточного отношения находится из условий вписывания корпуса редуктора в заданный габарит приближения верхнего строения пути и размеров, характеризующих конструктивные особенности редуктора (рис. 5.4).

Определяем максимально возможный диаметр вершин зубьев зубчатого колеса:

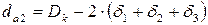; (5.3)

где 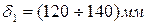– клиренс; 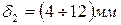– толщина нижней стенки корпуса редуктора; 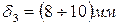– расстояние между вершинами зубьев и нижней стенкой редуктора.

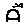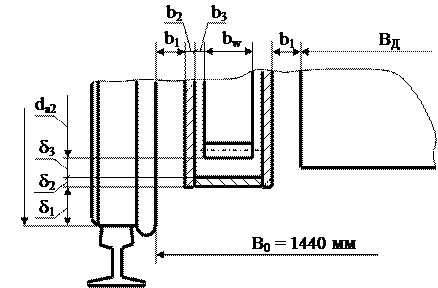Рис. 5.4. Схема вписывания тягового редуктора

Значения величин выбираются из следующих соображений. Величина клиренса 120мм согласно ГОСТ является минимальной для неподрессоренных элементов ходовой части подвижного состава. Клиренс 140мм должен быть обеспечен для подрессоренных элементов ходовой части. Следовательно, для приводов первого и второго класса с опорно-осевым (неподрессоренным) редуктором следует задаваться значением клиренса 120мм, а для привода третьего класса с опорно-рамным (подрессоренным) редуктором значением клиренса 140мм. Толщина нижней стенки корпуса редуктора для ненесущих корпусов в приводах первого и третьего классов выбирается в пределах 4…9мм, для несущих корпусов в приводе второго класса 10…12мм.

В соответствии с рекомендациями [Камаев], значение модуля 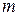зубчатого зацепления принимается 9-10мм, если крутящий момент на колесной паре не превышает 20 кНм, при большем моменте принимают модуль 11-12мм.

Диаметр делительной окружности зубчатого колеса определяется как

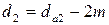; (5.4)

где 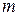– модуль зацепления.

Число зубьев зубчатого колеса находится из соотношения

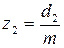. (5.5)

Как правило, предварительный расчет количества зубьев дает дробное число. Поэтому для дальнейшего расчета принимается округленное до целого числа в меньшую сторону количество зубьев. Например, в результате расчета получено число зубьев 79,33. Для дальнейшего расчета следует принимать число зубьев 79. Необходимость округления числа зубьев колеса в меньшую сторону связано с тем, что большее их число при заданном модуле приведет к увеличению диаметра вершин зубьев и уменьшению ранее принятых величин .

Задавшись целым числом зубьев колеса 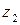, уточняем значение его делительного диаметра .

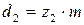Число зубьев шестерни находится из соотношения

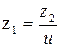. (5.6)

Предварительный расчет числа зубьев шестерни, также дает дробное число. Для шестерни количество зубьев следует округлять в большую сторону. Например, было получено значение числа зубьев шестерни 20,52. Для дальнейшего расчета принимаем число зубьев 21.

Задавшись целыми значениям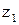и и 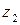, уточняем значение передаточного отношения редуктора

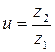. (5.7)

Определяем значение делительного диаметра шестерни

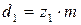. (5.8)

Рассчитываем межосевое расстояние передачи

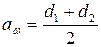. (5.9)

Размещение элементов передачи в габаритах ограниченных расстоянием между колесами определяется следующими размерами: В_Д – длина корпуса тягового двигателя; b₁ – расстояние от стенок редуктора до колеса и тягового двигателя должно быть не менее 30мм; b₂ – толщина боковой стенки корпуса редуктора выбирается аналогично величине 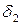; b₃ – расстояние между торцом зубчатого колеса и внутренней стенкой корпуса редуктора принимается равным 10мм;
b_w – ширина зубчатого венца принимается равной 120мм, при осевой мощности локомотива до 900 кВт, при осевой мощности более 900 кВт ширина венца принимается равной 140мм.

Задаваясь величинами b₂, b₃ и b_w определяем ширину корпуса редуктора

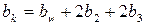. (5.10)

По выбранным и рассчитанным габаритным размерам элементов тяговой передачи выполняется эскиз компоновки колесно-моторного блока (рис 5.5).

5.2.2. Привод второго класса

Предварительный расчет передаточного отношения и проверка на достижение конструкционной скорости производится аналогично приводу первого класса по формулам (5.1) и (5.2). Затем по формуле (5.3) определяется максимально возможный диаметр вершин зубьев зубчатого колеса.

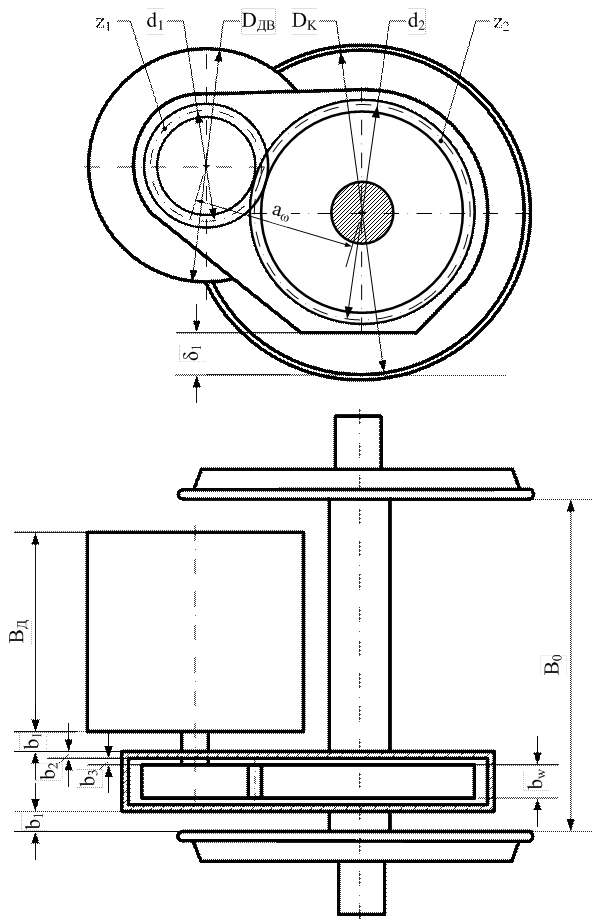
Рис. 5.5. Компоновка тяговой передачи первого класса.

Значения величин и выбираются согласно рекомендациям приведенным выше. По формуле (5.4) определяется делительный диаметр зубчатого колеса.

Далее последовательность расчета параметров привода второго класса имеет ряд отличий в силу более сложной схемы сопряжения элементов привода по линии централи. Схема сопряжения приведена на рис. 5.6.

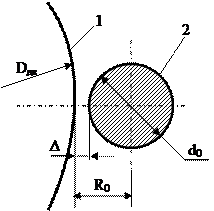
Рис. 5.6. Схема сопряжения элементов тяговой передачи в приводе второго класса: 1 – корпус тягового двигателя; 2 – ось колесной пары.

Для привода второго класса приведенные размеры, по данным [Щербаков] имеют следующие значения: d₀ = 200 мм, Δ = 10 мм, R₀ = 110 мм.

По схеме, межосевое расстояние передачи:

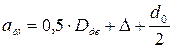; (5.11)

где 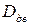– наружный диаметр остова тягового двигателя; Δ – зазор между остовом тягового двигателя и колесной парой; d₀ – диметр оси колесной пары.

Число зубьев зубчатого колеса находим по формуле (5.5), округляем до целого числа в меньшую сторону и уточняем значение делительного диаметра.

Определяем делительный диаметр шестерни

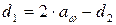; (5.12)

Число зубьев шестерни определяется по формуле

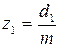. (5.13)

Полученное значение числа зубьев округляем до целого числа в большую сторону. По формуле (5.7) уточняем передаточное отношение.

При размещении элементов передачи в габаритах ограниченных расстоянием между колесами следует учитывать также размеры тяговой муфты расположенной между тяговым двигателем и редуктором. Ширина муфты В_М принимается 120 мм. Расстояния b₄ от тяговой муфты до тягового двигателя и корпуса редуктора должны быть не менее 30 мм.

Эскиз компоновки привода второго класса приведен на рис 5.7.

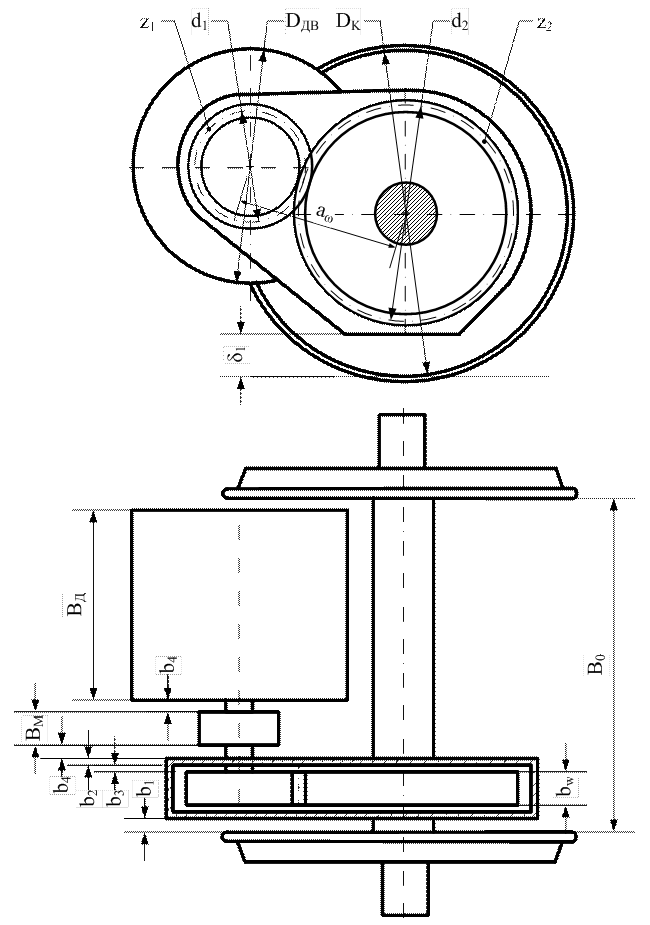
Рис. 5.7. Компоновка тяговой передачи второго класса.

5.2.3. Привод третьего класса

Основные параметры привода третьего класса производится аналогично приводу второго класса. По формулам (5.1) и (5.2) предварительно рассчитывается передаточное отношение и проводится проверка на достижение конструкционной скорости. По формуле (5.3) определяется максимально возможный диаметр вершин зубьев зубчатого колеса. Выбираются значения величин и 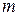. По формуле (5.4) определяется делительный диаметр зубчатого колеса. Полученное значение делительного диаметра необходимо уменьшить на 30…100 мм. Это связано с тем, что подрессоривание редуктора в приводе третьего класса создает дополнительные ограничения по приближению верхнего строения пути. Вследствие увеличения минимального значения клиренса до 140 мм, необходимо уменьшить предельный диаметр зубчатого колеса по сравнению с его диаметром в приводах первого и второго класса. Наличие зазора между полым валом привода и осью колесной пары приводит к увеличению централи. Эти конструктивные особенности привода третьего класса приводят к уменьшению максимально возможного передаточного отношения, что не играет большой роли для пассажирских локомотивов, но ограничивает использование локомотивов с приводом третьего класса в грузовой службе.

Для определения межосевого расстояния рассмотрим схему сопряжения элементов передачи третьего класса по линии централи (рис.5.8).

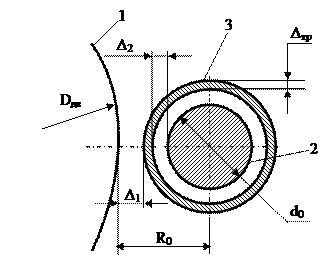
Рис. 5.8. Схема сопряжения элементов тяговой передачи в приводе третьего класса: 1 – корпус тягового двигателя; 2 – ось колесной пары; 3 – полый вал.

Для привода второго класса приведенные на схеме размеры, по данным [6] имеют следующие значения: d₀ = 200 мм, Δ₁ = 7 мм, Δ₂ = 35 мм, Δ_тр = 15 мм.

Таким образом, межосевое расстояние передачи:

;

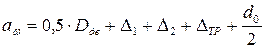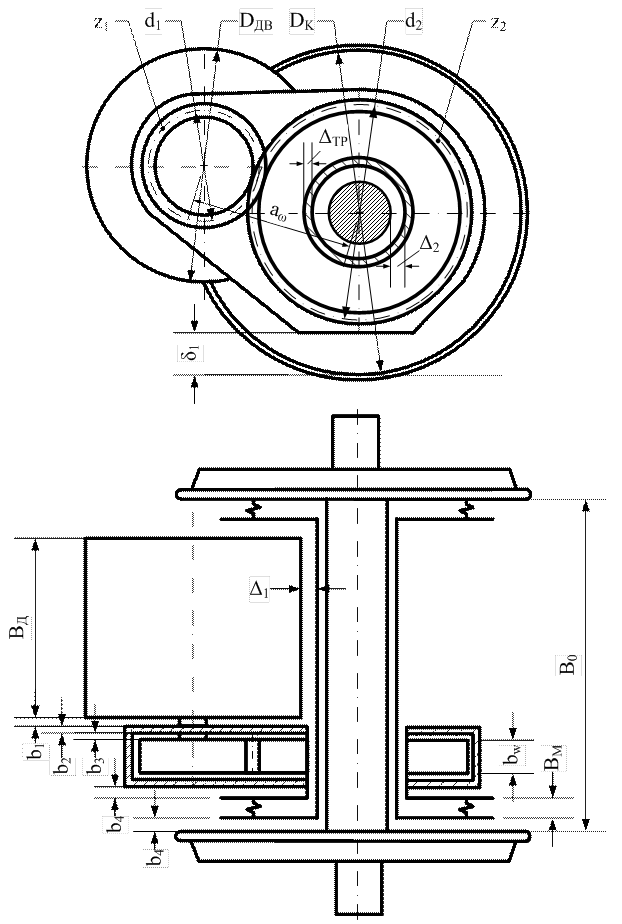Рис. 5.9. Компоновка тяговой передачи третьего класса.

где 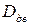– наружный диаметр остова тягового двигателя; 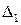– расстояние между остовом тягового двигателя и полым валом; 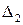– расстояние между полым валом и осью колесной пары; 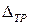– толщина стенки полого вала; 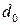– диаметр оси колесной пары.

Число зубьев зубчатого колеса находим по формуле (5.5), округляем до целого числа в меньшую сторону и уточняем значение делительного диаметра.

Определяем делительный диаметр шестерни по формуле (5.12).

Число зубьев шестерни определяется по формуле (5.13). Полученное значение числа зубьев округляем до целого числа в большую сторону.

По формуле (5.7) уточняем передаточное отношение.

При компоновке передачи третьего класса необходимо учитывать размеры муфт соединяющих зубчатое колесо с полым валом и полый вал с колесной парой. Ширина муфт В_М принимается 100 мм. Расстояния от тяговых муфт до сопрягаемых элементов привода должны быть не менее 30 мм.

Эскиз компоновки привода третьего класса приведен на рис 5.9.