Правило 3. Критерий окончания поиска
Поиск завершается, когда или размеры симплекса, или разности между значениями функции в вершинах становятся достаточно малыми. Чтобы можно было применять эти правила, необходимо задать величину параметра окончания поиска.
Реализация изучаемого алгоритма основана на вычислениях двух типов: (1) построении регулярного симплекса при заданных базовой точке и масштабном множителе и (2) расчете координат отраженной точки. Построение симплекса является достаточно простой процедурой, так как из элементарной геометрии известно, что при заданных начальной (базовой) точке х(0) и масштабном множителе α координаты остальных N вершин симплекса в N-мерном пространстве вычисляются по формуле
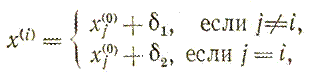 (3.13)
(3.13)
для i и j=1, 2, 3,…,N.
Приращения δ1 и δ2, зависящие только от N и выбранного масштабного множителя α, определяются по формулам
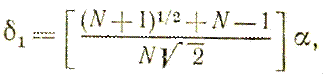 (3.14)
(3.14)
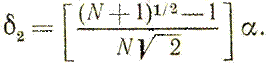 (3.15)
(3.15)
Заметим, что величина масштабного множителя α выбирается исследователем, исходя из характеристик решаемой задачи. При α — 1 ребра регулярного симплекса имеют единичную длину.
Вычисления второго типа, связанные с отражением относительно центра тяжести, также представляют несложную процедуру. Пусть x 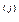 точка, подлежащая отражению. Центр тяжести остальных N точек расположен в точке
точка, подлежащая отражению. Центр тяжести остальных N точек расположен в точке
x 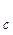 =
= 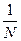
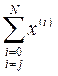 . (3.16)
. (3.16)
все точки прямой, проходящей через x 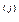 и хc, задаются формулой
и хc, задаются формулой
х = x 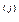 + λ(хc – x
+ λ(хc – x 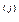 ). (3.17)
). (3.17)
При λ = 0 получаем исходную точку x 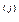 тогда как значениеλ =1 соответствует центру тяжести хc. Для того чтобы построенный симплекс обладал свойством регулярности, отражение должно быть симметричным. Следовательно, новая вершина получается при λ= 2. Таким образом,
тогда как значениеλ =1 соответствует центру тяжести хc. Для того чтобы построенный симплекс обладал свойством регулярности, отражение должно быть симметричным. Следовательно, новая вершина получается при λ= 2. Таким образом,
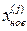 = 2
= 2 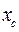 –
– 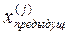 (3.18)
(3.18)
Изложенный выше алгоритм S2-метода имеет несколько очевидных преимуществ.
1. Расчеты и логическая структура метода отличаются сравнительной простотой, и, следовательно, соответствующая программа для ЭВМ оказывается относительно короткой.
2. Уровень требований к объему памяти ЭВМ невысокий, массив имеет размерность (N + 1, N + 2).
3. Используется сравнительно небольшое число заранее установленных параметров: масштабный множитель α, коэффициент уменьшения множителя α (если применяется правило 2) и параметры окончания поиска.
4. Алгоритм оказывается эффективным даже в тех случаях, когда ошибка вычисления значений целевой функции велика, поскольку при его реализации оперируют наибольшими значениями функции в вершинах, а не наименьшими.
Перечисленные факторы характеризуют метод поиска по симплексу как весьма полезный при проведении вычислений в реальном времени.
Алгоритм обладает также рядом существенных недостатков.
Не исключено возникновение трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса зависят от одного и того же масштабного множителя α. Чтобы обойти трудности такого рода, в практических задачах следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине.
Алгоритм работает слишком медленно, так как полученная на предыдущих итерациях информация не используется для ускорения поиска.
Не существует простого способа расширения симплекса, не требующего пересчета значений целевой функции во всех точках образца. Таким образом, если ос по какой-либо причине уменьшается (например, если встречается область с узким «оврагом» или «хребтом»), то поиск должен продолжаться с уменьшенной величиной шага.
Модифицированная процедура поиска по симплексу, разработанная Нелдером и Мидом, частично устраняет некоторые из перечисленных недостатков.

a — нормальное сжатие (θ = α = 1), f 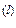 < f(x
< f(x  ) < f
) < f 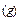 ; б — растяжение (θ = γ > 1), f(x
; б — растяжение (θ = γ > 1), f(x 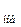 ) < f
) < f 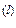 , в — сжатие (θ = β < 0), f(x
, в — сжатие (θ = β < 0), f(x 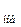 ) > f
) > f 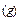 , f(x
, f(x 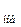 ) ≥ f
) ≥ f 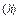 ; г — сжатие (θ = β > 0) f
; г — сжатие (θ = β > 0) f 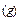 < f(x
< f(x 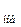 ) < f
) < f 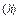 .
.
Рисунок 3.3 - Растяжение и сжатие симплексов
Нетрудно заметить, что хотя формула для определения вершин регулярного симплекса оказывается весьма удобной при построении исходного образца, однако веских оснований для сохранения свойства регулярности симплекса в процессе поиска нет. Следовательно, при отражении симплекса существует возможность как его растяжения, так и сжатия. При расчетах по методу Нелдера и Мида используются вершины симплекса x(h) (которой соответствует наибольшее значение целевой функции f(h) ), х(g) (которой соответствует следующее по величине значение целевой функции f(g) )и х(l) (которой соответствует наименьшее значение целевой функции f(l) ) - Напомним, что отражение вершины симплекса осуществляется по прямой
х = x 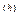 + λ(хc – x
+ λ(хc – x 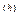 ).
).
или х = x 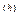 + (1 + θ)(хc – x
+ (1 + θ)(хc – x 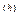 ). (3.19)
). (3.19)
При θ = 1 имеет место так называемое нормальное отражение симплекса, поскольку точка хнов располагается на расстоянии || хс – x(j) || от точки хс.Если –1 ≤ θ < 1, то наблюдается сжатое отражение, или сжатие симплекса, тогда как выбор θ >1 обеспечивает растянутое отражение, или растяжение симплекса. На рис. 3.3 приведены возможные варианты отражения. Три значения параметра θ, используемые при нормальном отражении, сжатии и растяжении, обозначаются через α,βиγсоответственно. Реализация метода начинается с построения исходного симплекса и определения точек x(h), х(g), х(l), хc. После нормального отражения осуществляется проверка значений целевой функции по критерию окончания поиска в точках отраженного симплекса. Если поиск не закончен, то с помощью тестов, приведенных на рис. 3.3, выбирается одна из операций —нормальное отражение, растяжение или сжатие. Итерации продолжаются, пока изменения значений целевой функции в вершинах симплекса не станут незначительными. В качестве удовлетворительных значений параметров α, β иγ Нелдер и Мид рекомендуют использовать α = 1, β = 0,5 и γ= 2.
Результаты отдельных численных экспериментов показывают, что метод Нелдера — Мида обладает достаточной эффективностью и высокой надежностью в условиях наличия случайных возмущений или ошибок при определении значений целевой функции. В 1969 г. Бокс и Дрейперутверждали, что этот метод является «наиболее эффективным из всех известных методов последовательной оптимизации». В 1972 г. Паркинсон и Хатчинсон исследовали влияние выбора параметров α,β иγ и способа построения исходного симплекса на эффективность поиска. Они установили, что ориентация исходного симплекса в отличие от его формы является существенным фактором, влияющим на процедуру поиска, и предложили использовать значения параметров (α, β, γ) = (2, 0,25, 2,5). Такой выбор параметров позволил обеспечить хорошую работу алгоритма при повторении последовательных растяжений симплекса.
