Понятие о напряженном состоянии грунта.

Прочность и устойчивость сооружений – опр-ся напряжениями, которые возникают под действием внешних нагрузок и свойствами г.п.

По изменению напр сост массива опр-т сферу взаимодействия с инж сооруж для расчета напряжений исп-т ур-е теории упругости, которые м.б использованы для любых линейно деформируемых тел в этом случае зоны пластич деформаций либо отсутствуют, либо имеют незначительную глубину развития.

На грунты действуют два вида сил:

- объемные (природные) - сила тяжести, сила магнитного воздействия, сила элек поля, фильтрационные силы.

- поверхностные (внешние) – силы регулируемые, управляемые – давление.

Объект механики грунтов выражается в кг/см², Па, МПа, Т/м².

Поверх силы оказывают влияние на основания, вызывая напряжения в последних.

Напряжения – интенсивность распр-я внутр усилий в выделенном элементе породы. Чтобы рассчитать деформации нужно знать величину напряжений.

Все внешние силы делятся:

- сосредоточенные – идеализированное предст о силе (кг*с, Н)

- распределенные – приложена к площади (кг*с/см², Па, МПа, Т/м²)

Величина напряжений зависит от внешней силы Р, от координаты точки в которой мы определяем напряжения, от направления площадки, для которой определяется напряжение. Опр-ся по формуле: σ = P/S.

Напряжения направленные перпендикулярно к рассмат-й площадке – нормальные: σ_n= σ sinα;

А в плоскости площадки – касательные: τ = σ_α cosα.

Расчет осадки в условиях одномерного сжатия.

Выполняют в том случае, если соотношение мощности сжимаемого слоя h и ширины фундамента b не превышает одной четверти, т. е. h/b 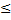0,25. Одноразмерное сжатие возникает, например, если на небольшой глубине от подошвы фундамента залегает практически несжимаемый слой горной породы, либо когда нагрузка на породу распределена по большой площади или при намыве территории, предназначенной для хозяйственного освоения.

Нормальные напряжения, возникающие в породе при одноразмерном сжатии в результате приложения к ее поверхности вертикальной равномерно распределенной нагрузки, по глубине не меняются и равны интенсивности распределения внешней нагрузки (σ_z=p).

S= ; S=h₁ε_z= где а – коэф сжимаемости; Е – модуль деформации; – интервал давлений; – коэф пористости до уплотнения; μ – коэф поперечной деформации; h₁ – высота призмы породы до уплотнения, равная мощности сжимаемого слоя; ε_z –относительная осадка призмы, ε_z= ;(значения снимаются с компрессионных кривых). Если принять = р и обозначить множитель , выражение для расчета осадки будет иметь вид: S= .

Выражение для расчета осадки при одноразмерном сжатии можно быть получено также исходя из анализа зависимостей обобщенного закона Гука:

ε_z

ε_y =

ε_x=

В случае одноразмерного сжатия деформации от действия нормальных составляющих напряжения по вертикальным площадкам и отсутствуют, поэтому ε_x= ε_y=0, =

Расчет осадки во времени.

Осадка сооружений может развиваться в течение длительного промежутка времени. Устойчивость сооружений тесно связана с решением задач о характере уплотнения породы во времени.

Медленная неравномерная пластичная деформация горной породы под воздействием постоянной нагрузки называется ползучестью горной породы.

Возможность уплотнения породы во времени под действием давления от собственного веса сооружения определяет также величину сопротивления сдвигу пород основания, особенно глинистых отложений.

Процесс протекания осадок глинистых пород во времени и их величина зависят от: 1. От степени литофицированности грунтов. 2. От степени водонасыщенности грунтов. 3. От характера перераспределения давления между скелетом и поровой водой.

В общем случае величина осадки пород основания во времени S(t) равна сумме составляющих уплотнение при оттоке (фильтрации) воды из породы S_ф(t) и ползучести скелета породы S_п(t):

S(t)= S_ф(t)+ S_п(t)

Расчет осадки с использованием теории фильтрационной консолидации. 1. В полностью водонасыщенной породе все составные части несжимаемы. 2. Фильтрация в породе происходит с законом Дарси. 3. К_ф- величина const. 4. В породе отсутствуют структурные связи и внешнее давление считается приложенным мгновенно и вызывает возникновение пор. 5. Сопротивление сдвигу отсутствует по этому после приложения нагрузки начинается фильтрация воды из породы. 6. В скелете породы не возникают деформации ползучести, сразу после удаления воды осадка стабилизируется.

P=P_ск+H*ɤ_в

Закон Дарси υ = -kI= -k₀(δH/δz₀) δ-эта хуйня в другую сторону пишется

Продифференцировав получим:

δH/dt=C_u(δ2H/δz₀² )

C_u-коэфф консолидации С_u=K*(1+l₀)/a*ɤ_b

Это дифференциальное уравнение решается с помощью рядов Фурье и при граничных условиях: 1. t=0,0<z<h, H=P/γ_b 2. t=0, z=0, z=h

H=4P/πγ_b*сумму1/m*e^-mTy*sin mπz/h

S₀(t)=S_k*u u-степень уплотнения грунтов. S_k-конечная осадка T_u=π²*C_u/4h² – величина фактора времени. Время уплотнения двух разных по мощности, но одинаковых по свойствам слоёв можно определить: t₁/t₂=(h₁/h₂)²