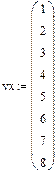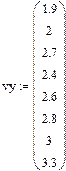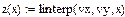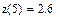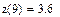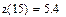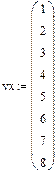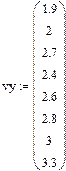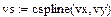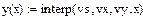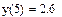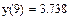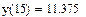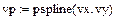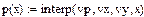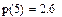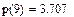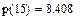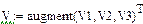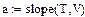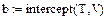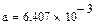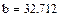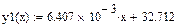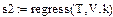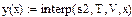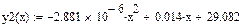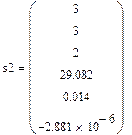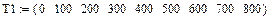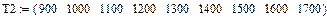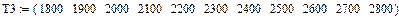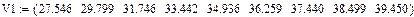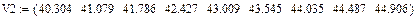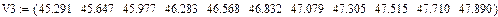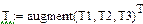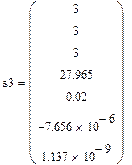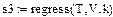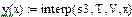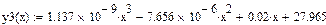1. Вводим векторы 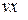 и
и 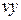 , которые являются координатами экспериментальных точек.
, которые являются координатами экспериментальных точек.
2. Осуществляем интерполяцию с помощью встроенной функции
f(x)=linterp(vx,vy,x).
3. Используем интерполяцию для построения графика функции и вычисления ее значения в любых точках.
Алгоритм сплайн-интерполяции
1. Вводим векторы 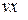 и
и 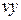 , которые являются координатами экспериментальных точек.
, которые являются координатами экспериментальных точек.
2. Осуществляем интерполяцию с помощью встроенных функций
vs=cspline(vx, vy)- возвращает вектор vs вторых производных при приближении в опорных точках к кубическому полиному.
vs=pspline(vx,vy)- )- возвращает вектор vs вторых производных при приближении в опорных точках к параболе.
vs=lspline(vx, vy) - возвращает вектор vs вторых производных при приближении в опорных точках к прямой.
f(x)=interp(vs, vx, vy, x) - возвращает интерполированную функцию в точке х.
3. Используем интерполяцию для построения графика функции или вычисления ее значения.
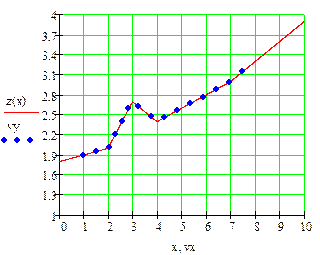
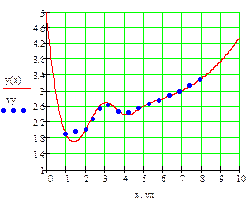
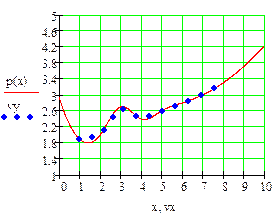
Пример. 1.По экспериментальным точкам, координаты которых представлены в таблице, выполнить линейную и сплайн-интерполяцию и найти трассировкой значение функции в точках x=5, x=9
| xi | | | | | | | | |
| yi | 1.9 | 2.0 | 2.7 | 2.4 | 2.6 | 2.8 | 3.0 | 3.3 |
►
Линейная интерполяция
Сплайн – интерполяция
◄
Полиноминальная регрессия
Полиномная регрессия осуществляется комбинацией встроенных функций:
regress(x,y,k) —
interp(s,x,y,t) —
s= regress(x,y,z) —
x— вектор данных аргумента;
y— вектор данных значений функции;
k— степень полинома регрессии;
t— значение аргумента полинома.
Ниже приведен пример нахождения полиномиальной регрессии по экспериментальным данным зависимости теплоемкостей газа от температуры ДВС.
| Ввод данных в виде слияния трех матриц |
| Линейная регрессия y=ax+b |
План выполнения работы
1. Выполните примеры из описания лабораторной работы.
2. По данным эксперимента выполните линейную и сплайн-интерполяцию, находя вектор вторых производных при приближении в опорных точках к прямой, параболе, кубической параболе.
| xi | N | N+2 | N+3 | N+4 | N+5 | N+6 | N+7 |
| yi | | | | | | | |
Построить графики интерполирующих функций и найдите значения этих функций в точках x=N+5, x=N+7, x=N+10.
Контрольные вопросы
1. Что такое аппроксимация и интерполяция?
2. Какие отличия между линейной и сплайн-интерполяцией?
3. Назовите встроенные функции, применяемые для линейной и сплайн-интерполяции.
Лабораторная работа №8
Статистическая обработка данных в MathCAD
Цель работы: познакомиться со статистическими расчетами с данными.
Ввод данных
При решении практических задач статистического анализа данные представляют собой экспериментальные данные. Эти данные могут быть введены заранее и сохранены в файле. Чтение и запись чисел осуществляется с помощью функции доступа: xi=READ(имя файла). При небольшом объеме данные вводятся в виде матрицы-строки А.
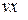 и
и 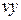 , которые являются координатами экспериментальных точек.
, которые являются координатами экспериментальных точек.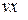 и
и 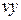 , которые являются координатами экспериментальных точек.
, которые являются координатами экспериментальных точек.