Цель работы: научиться вводить массивы, выполнять действия с матрицами и векторами, решать системы линейных уравнений.

Создание массива

Самый простой способ создания массива чисел состоит в создании массива из пустых полей и их последующем заполнении.

Для этого:

Выберите Матрицы из меню Вставка (или нажмите Ctrl+M), чтобы вызвать диалоговое окно.

1. Определите в нём нужное количество строк и столбцов.

2. Нажмите "OK" , чтобы создать массив пустых полей.

3. Щёлкните на поле, чтобы выделить его, затем введите требуемое значение. Для перемещения между полями можно также использовать клавишу «Tab».

При определении больших массивов, для каждого элемента которых существует формула, через которую он выражается, удобнее использовать дискретные аргументы. Пример приводится ниже:

i:=1..9 j:=1..9

X[i,j]:=i²+j

Извлечение элементов, строк и столбцов

Чтобы обратиться к отдельному элементу массива, добавьте к имени массива нижние индексы и напечатайте знак равенства. Например:

Чтобы обратиться к целому столбцу, добавьте к имени массива верхний индекс, как показано ниже:

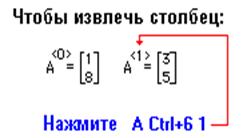
Чтобы обратиться к целой строке, нужно добавить верхний индекс к транспонированному массиву, как показано ниже:

Действия над матрицами

Линейные операции над матрицами, умножение матриц, нахождение обратной и транспонированной матриц, векторное, скалярное произведение векторов, вычисление определителя матрицы можно выполнять с помощью арифметических операций с клавиатуры или пиктограмм Calculator(Калькулятор) и Matrix (Матрица).

Для этого нужно выбрать пункт меню: Вид->Панели инструментов->Матрицы появится панель следующего вида:

На панели расположены кнопки, на которых «изображено» действие, выполняемое при ее нажатии.

Встроенные функции

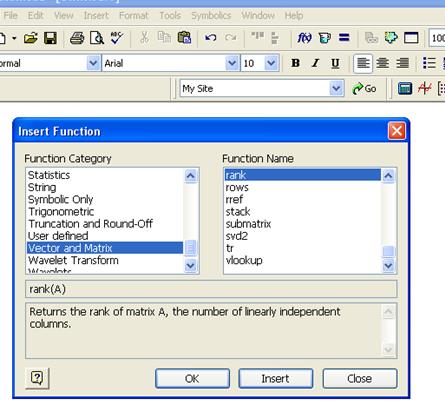
Mathcad содержит огромное количество встроенных функций. Для вставки функции в документ можно использовать диалоговое окно Insert Function,которое вызывается нажатием кнопки с надписью f(x)на стандартной панели инструментов. Встроенные матричные функции находим в разделе Vector and Matrix:

augment(A,B,C) —

stack(A,B) —

rank(A) —

max(A) — Возвращает наибольший элемент в A.

min(A) — Возвращает наименьший элемент в A.

tr(M) — Возвращает сумму элементов на диагонали квадратной матрицы M.

eigenvec(M,z) — Возвращает нормированный собственный вектор матрицы M, соответствующий собственному значению z.

eigenvals(M) — Возвращает вектор, элементами которого являются собственные значения матрицы M.

eigenvecs(M) —Возвращает матрицу, столбцами которой являются собственные векторы матрицы M.

Чтобы выполнить действия с комплексными числами, предварительно вводится мнимая единица:

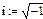Пример 1.Даны векторы: 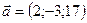и .

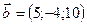Найти длину вектора 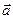, векторное, скалярное произведение векторов 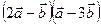, смешанное произведение .

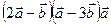►Вводим векторы как матрицы столбцы, длину вектора находим с помощью оператора 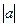на пиктограмме Calculator(Калькулятор), остальные операции находим на пиктограмме Matrix (Матрица).

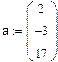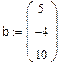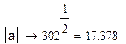Длина вектора

Векторное, скалярное и смешанное произведение:

◄

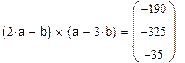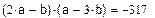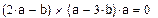Пример 2.Найти расстояние между точкам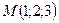и и .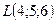

►

►

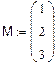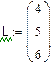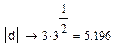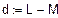Пример 3. выполнить действия с комплексными числами: .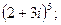

►

◄
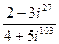
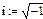
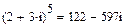
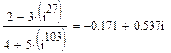