Алгоритм отделения корней методом последовательного перебора
Сущность метода.Большая производительность современных ЭВМ дает возможность отделить все действительные корни уравнения методом последовательного перебора. Нижнюю границу А и верхнюю границу В корней уравнения выбирают приблизительно, исходя из физического содержания задачи, описываемой решаемым уравнением, или из графика функции у= F(х). В основе этого метода лежит теорема 1: выбирается начальное значение х = А, затем с фиксированным шагом 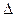 х = Н вычисляются значения функции F в точках А+kН (k = 0), 1, 2,...) до тех пор, пока она не изменит знак. Пусть, например, после n-го шага в точке х = А+nН функция F сменила знак, тогда [А+(n--1)Н; А+nН] - отрезок изоляции корня, P=А + nH -
х = Н вычисляются значения функции F в точках А+kН (k = 0), 1, 2,...) до тех пор, пока она не изменит знак. Пусть, например, после n-го шага в точке х = А+nН функция F сменила знак, тогда [А+(n--1)Н; А+nН] - отрезок изоляции корня, P=А + nH - 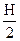 - приближенное значение корня уравнения с точностью e =
- приближенное значение корня уравнения с точностью e = 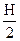 , то есть |x - P| £
, то есть |x - P| £ 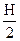 . Правый конец этого отрезка принимают за начальное значение следующего корня, если он есть. Такое продвижение вправо по оси Ох продолжают до тех пор, пока не достигнут верхней границы корней В. Этот алгоритм последовательного перебора требует большого объема вычислительной работы, обусловленного многократным вычислением значения функции F с шагом Н. Естественно, что для ручных вычислений он непригоден. Основной проблемой является выбор шага.
. Правый конец этого отрезка принимают за начальное значение следующего корня, если он есть. Такое продвижение вправо по оси Ох продолжают до тех пор, пока не достигнут верхней границы корней В. Этот алгоритм последовательного перебора требует большого объема вычислительной работы, обусловленного многократным вычислением значения функции F с шагом Н. Естественно, что для ручных вычислений он непригоден. Основной проблемой является выбор шага.
Цель алгоритма - отделить корни и найти их грубые приближенные значения. Следует отметить, что метод последовательного перебора не дает полной гарантии, что ни один из корней уравнения не будет потерян, особенно в тех случаях, когда корни достаточно близки друг к другу, а шаг не слишком мал. В таких случаях надо произвести новый просчет с более мелким шагом Н.
Алгоритмы уточнения корня
1. Алгоритм уточнения корня методом половинного деления
Сущность метода.Пусть каким-либо методом найден отрезок изоляции корня [а; b] уравнения F(х) = 0, где F(х) - непрерывна на участке [a; b], (а)*F(b) < 0. В дальнейшем требуется сузить этот отрезок так, чтобы его длина стала не больше заранее заданной точности вычисления корня e, то есть чтобы |b - a| £ e.
Этот процесс сужения интервала, содержащего изолированный корень уравнения F(х) = 0, называется уточнением корня.
В этом алгоритме отрезок изоляции корня [а; b] точкой с = 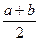 делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F
делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F  принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 =
принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 = 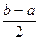 . С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
. С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
§ либо найдется такая точка cn = 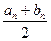 , в которой F(cn) = 0 (что маловероятно!), и задача решена;
, в которой F(cn) = 0 (что маловероятно!), и задача решена;
§ либо такой точки не найдется, но при некотором n придем к отрезку [an, bn] длины bn - an = 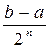 £ e, содержащему в себе искомый корень.
£ e, содержащему в себе искомый корень.
Тогда числа an и bn являются приближенными значениями искомого корня с требуемой точностью e соответственно с недостатком и с избытком. Однако лучше за приближенное значение искомого корня взять число сn = 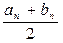 , погрешность которого не превышает
, погрешность которого не превышает 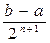 .
.
2. Алгоритм уточнения корня методом хорд
Сущность метода. Пусть отрезок изоляции [a; b] корня х уравнения F(х) = 0 найден, причем для определенности пусть F(a) < 0, F(b) > 0 и F'(х) > 0. График функции y = F(х) проходит через точки A(a; F(a)) и B(b; F(b)) (рис. 1). Составим уравнение хорды АВ как прямой, проходящей через точки А и В:
y = kx + l;
F(a) = ka + l;
F(b) = kb + l;
k = 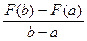 ; l = F(a) - a
; l = F(a) - a 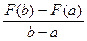
y= 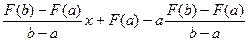
y - F(a) = 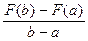 (x - a).
(x - a). 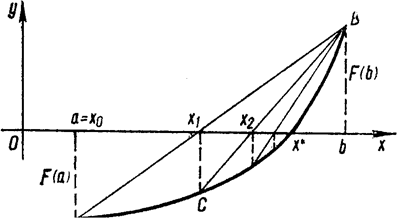
Рисунок 1 – Графическое представление метода хорд
далее находим абсциссу x1 точки пересечения хорды АВ с осью Ох, уравнение которой y = 0: 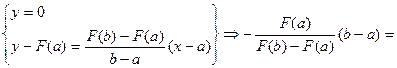
= x1 - a Þ x1 = a - 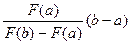 .
.
Число x1 примем за первое приближение корня х*. Далее, применяя этот же прием к отрезку изоляции [x1; b], на концах которого функция F(x) принимает противоположные знаки, получим второе приближение корня x2:
x2 = x1 - 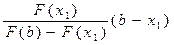
Этот процесс можно продолжать неограниченно. Описанный процесс называется методом хорд. В результате получим последовательность вложенных отрезков[a; b] É [x1; b] É [x2; b] É ... É [xn; b] É ...с неподвижным концом b. Последовательные приближения xn (n = 1, 2, ...) к точному значению корня х* вычисляются по формуле
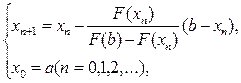 (3)
(3)
называемой формулой метода хорд, и образуют монотонно возрастающую последовательность a = x0 < x1 < x2 < ... < xn < xn+1 < ... < b, ограниченную сверху числом b. По теореме Вейерштрасса эта последовательность имеет предел
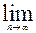 xn =
xn = 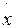 *.
*.
Поскольку F(х) непрерывна на [а; b], то 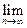 F(xn) = F(
F(xn) = F( 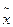 *).
*).
Переходя теперь к пределу в равенстве (3), получаем
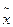 * =
* = 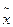 * -
* - 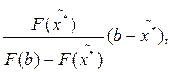
откуда, так как b - 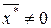 , следует, что F(
, следует, что F( 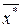 ) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х*, то х* = х*.
) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х*, то х* = х*.
Поскольку полученная последовательность (х„) сходится к корню уравнения х*, то любой ее член можно рассматривать в качестве приближенного значения корня. Практически последовательные приближения вычисляют до тех пор, пока не получат приближенное значение корня с требуемой точностью.
3.Алгоритм уточнения корня методом касательных
Сущность метода.Пусть [а; b] — отрезок изоляции корня х* уравнения F(х) = 0. И пусть для определенности F(a)<0, F(b)>0, F‘(x)>0 и F”(x)>0, xÎ[а; b], то есть производные сохраняют постоянный знак (рис.2). Идея метода касательных, предложенного Ньютоном, сводится к замене небольшой дуги
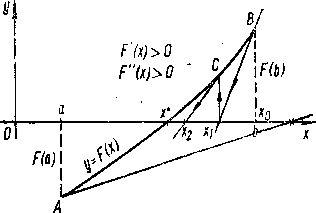
Рисунок 2 – Графическое представление метода касательных
кривой у = F(х) касательной к кривой, проведенной в некоторой точке интервала [а; b]. Выберем, например, x0 = b, так как F(x0) ´ F¢¢(x0)>0, и в точке В(x0, F(х0)) проведем касательную к кривой у = F(х). Ее уравнение:
y - F(x0) = F¢(x0)(x - x0).'
Найдем теперь точку пересечения x1 касательной с осью Ох(у = 0):
0 - F(x0) = F¢(x0)(x1 - x0) Þ x1 = x0 - 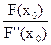
Эту точку x1 принимаем за первое приближение искомого корня х*. Через точку С(x1; F(x1)) снова проведем касательную y - F(x1) = F‘(x1)(x - x1), абсциссу точки пересечения которой с осью Ох примем за второе приближение х2 корня х*. Имеем:
0 - F(x1) = F‘(x1)(x2 - x1) Þ x2 = x1 - 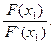
Продолжая этот процесс далее, получим рекуррентную формулу,
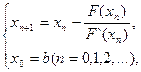 (8)
(8)
называемую формулой метода касательных.
Заметим, что если в рассматриваемом случае (F’(x) > О, F”(x) > О, F(b) > 0, F(а) < 0) касательную провести в точке А, то есть положить x0 = а, то точка пересечения ее с осью абсцисс может оказаться вне отрезка изоляции корня [a; b]. Это значит, что метод касательных неприменим, если в качестве начальной точки x0 выбрать такую, в которой F(x0) ´ F”(x0) < 0.
Как и в методе хорд, можно доказать (предлагаем читателю сделать это самостоятельно), что полученная числовая последовательность
x0>x1>x2>...>xn>xn+1>...>a
сходится к корню уравнения х*.
Для оценки погрешности приближения xn можно воспользоваться, как и в методе хорд, формулой
½x* - xn½ £ ½xn - xn-1½ £ e.
Анализируя возможные расположения кривой у = F(х)на отрезке изоляции, где последовательные приближения по методу касательных обозначены 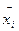 (i = 0,1,2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
(i = 0,1,2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
F(x0) F¢¢(x0) > 0 (9)
Пример 9. Методом касательных найти корень уравнения
F(x) = 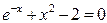
на отрезке [1; 2] с точностью до e = 10-5.
Находим: F‘(x) = - 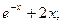 F¢¢(x) =
F¢¢(x) = 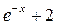 .
.
Применив формулу (8), имеем:
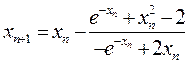 (n = 0, 1, 2, ...).
(n = 0, 1, 2, ...).
Выберем начальное приближение x0, используя условие (9). Имеем:
F(1) = 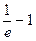 < 0;
< 0;
F(2) = 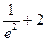 > 0;
> 0;
F¢¢(1) = 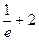 > 0;
> 0;
F¢(2) = 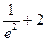 >0.
>0.
Поскольку F(2)´F”(2) > 0, то касательную следует проводить в правом конце отрезка, то есть x0 = b = 2.
Последовательные приближения вычисляем на ЭВМ, заполняя табл. 7.
| Xn | F(xn)= 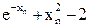 | F‘(xn)= 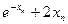 | 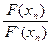 | ½xn – xn-1½ | |
| (2) - (5) | 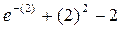 | e-(2)+2×(2) | 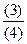 | ||
| 2,0 | 2,135335 | 3,864665 | 0,552528 | ||
| 1,5 | 0,473130 | 2,776870 | 0,170382 | 0,5 | |
| 1.38 | 0,033377 | 2,395523 | 0,013933 | 0,17 | |
| 1,316 | 0,000062 | 2,363794 | 0,000026 | 0,014 | |
| 1,8159738 | 0.0000005 | 2,3637346 | 0,0000002 | 0,0000262 | |
| 1,3159736 | - 0,0000005 | 2,3637342 | -0,0000002 | 0,0000002 |
Если в качестве приближенного значения корня взять число 1,3159736, то невязка F(1,3159737) = - 0,0000003.
4. Комбинированный метод хорд и касательных
Сущность метода.Рассмотренные выше метод хорд и метод касательных (каждый в отдельности) позволяют приблизиться к корню уравнения лишь с одной стороны: либо слева (приближение с недостатком), либо справа (приближение с избытком), причем всегда, если формула хорд дает приближение корня с недостатком, то формула касательных — с избытком, и наоборот. Одновременное применение этих двух методов на каждом шаге дает возможность искомый корень уравнения взять в вилку и не выпускать его из нее до достижения заданной точности.
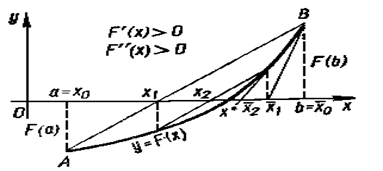
Рисунок 3 – Иллюстрация метода хорд и касательных
Пусть (рис.3) условие F( 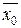 )×F«(
)×F«( 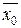 ) > 0 выполняется в правом конце отрезка изоляции корня (
) > 0 выполняется в правом конце отрезка изоляции корня ( 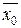 = b). Тогда последовательные значения с недостатком х0 = а, x1, x2, ... , xn, xn+1, ... вычисляют методом хорд:
= b). Тогда последовательные значения с недостатком х0 = а, x1, x2, ... , xn, xn+1, ... вычисляют методом хорд:
xn+1 = xn - 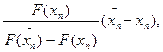 x0 = a(n = 0, 1, 2, ...), (10)
x0 = a(n = 0, 1, 2, ...), (10)
а последовательные значения корня с избытком
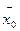 = b,
= b, 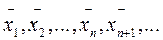
вычисляют методом касательных (8):
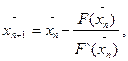
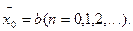 (11)
(11)
По формулам (10) и (11) вычисляют приближенные значения корня соответственно с недостатком и с избытком, причем для всех n xn < х* < хn.
Если при некотором n выполняется неравенство 0 < ½ 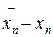 ½ £ e то в качестве приближенного значения искомого корня с точностью e принимают среднее арифметическое значение полученных двусторонних приближений, то есть x =
½ £ e то в качестве приближенного значения искомого корня с точностью e принимают среднее арифметическое значение полученных двусторонних приближений, то есть x = 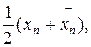 так как тогда½x - x*½ < ½
так как тогда½x - x*½ < ½ 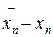 ½ £ e.
½ £ e.
Если условие 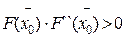 выполняется в левом конце отрезка изоляции корня, тогда
выполняется в левом конце отрезка изоляции корня, тогда
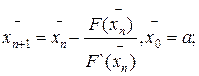 (12)
(12)
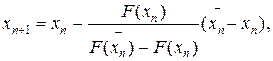 x0 = b (n = 0,1,2,...), (13)
x0 = b (n = 0,1,2,...), (13)
то есть формула касательных дает приближение корня с недостатком, а формула хорд—с избытком.
Обращаем внимание читателя на следующее обстоятельство. Если в формулах (3) и (7) метода хорд (его иногда называют стационарным методом хорд) один конец отрезка изоляции корня в процессе вычислений все время оставался неподвижным, то в формулах (10) и (13) комбинированного метода хорд и касательных оба конца отрезка изоляции корня являются подвижными. На каждом шаге вычислений в качестве неподвижного конца формулы метода хорд используется приближенное значение искомого корня, вычисленное по формуле метода касательных (рис. 22).
Пример. Комбинированным методом хорд и касательных найти корень уравнения
F(х) = Зх - cos х - 1 = 0 на отрезке [0; 1] с точностью e = 10-4
Так как F(х) непрерывная функция, a F’(x) = 3 +sin х > 0, х Î R; F(0) = -2 < 0 и F(1) = 2 - cos1 > 0, то на отрезке [0; 1] имеется единственный корень уравнения. Вторая производная
F”(x) = cos х> 0, х Î [0; 1].
Условие F(х)•F”(x) > 0 выполняется в точке х = 1, то есть F(1)•F(2) > 0. Следовательно, уточнение корня выполняем по формулам:
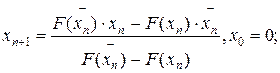
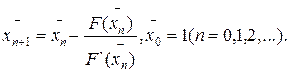
Вычисления на ЭВМ оформляем в табл. 8, в которую введены промежуточные графы, облегчающие вычисление значений функции и производной.
Таблица 8 Расчетная таблица метода хорд и касательных
| Xn | 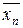 | 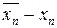 | F(xn) | 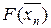 | 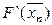 | 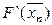 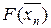 | 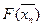 xn - F(xn) xn - F(xn) 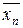 | |
| n | (9):(8) | (3) –(6): (7) | (3) - (2) | 3*(2) - соs(2) – 1 | 3*(3) – cos(3) - 1 | 3 + sin(3) | (6) - (5) | (6)*(2)- (5)*(3) |
| -2 | 1,459697 | 3,841471 | 3,459697 | |||||
| 0,5780853 | 0,6200162 | 0,0419309 | -0,1032551 | 0,0461796 | 3,581048 | 0,1494401 | 0,0907188 | |
| 0,6070577 | 0,6071207 | 0,0000630 | xср=0.5 ( 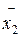 - x2) = 0,607089 - x2) = 0,607089 |
О точности полученных приближений (x2, 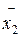 , xcp) можно судить по невязке:
, xcp) можно судить по невязке:
F(x2) = F(0,6070577) = - 0,0001569,
F( 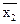 ) = F(0,6071207) = 0,0000681,
) = F(0,6071207) = 0,0000681,
F(xcp) = F(0,6071) = 0,000006.
5. Метод последовательных приближений (итераций)
Сущность метода. Для нахождения действительных корней уравнения F(x) = 0, где F(x) - непрерывная функция на [a; b], его заменяют равносильным уравнением
х = j(х) (14)
Это можно сделать всегда, притом не одним способом. Например, уравнение
х3 - 9х + 3 = 0
можно представить так: 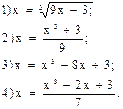
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня уравнения (14) берут: 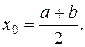 Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
xn+1 = j(xn), (n = 0, 1, 2, ...) (15)
Полученная последовательность х0, х1, ..., xn, xn+1,... называется итерационной последовательностью, способ построения ее называется методом последовательных приближений или методом итераций численного решения уравнения.
При пользовании методом итераций необходимо выяснить основной вопрос: сходится ли полученная последовательность (хn) к решению х* уравнения (14) при возрастании n? Если последовательность (хn) сходится, то есть существует предел х* = 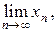 то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем:
то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем:
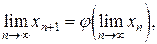 или x* = j(x*). (16)
или x* = j(x*). (16)
Следовательно, в этом случае х = х* является корнем уравнения х = j(х), а значит, и уравнения F(x) = 0.
Если же последовательность (хn) окажется расходящейся, то есть не существует конечного предела построенной последовательности приближений (хn), то это означает, что процесс итераций построен неудачно, и его надо заменить другим.
Следовательно, метод последовательных приближений применим при выполнении условия:
½j‘(x)½ £ M1 < 1 (18)
для всех х, принадлежащих отрезку изоляции корня уравнения (14), В этом случае процесс итераций сходится, и тем быстрее, чем меньше М1; если же ½j‘(x)½ > 1, то итерационный процесс расходится. Для конкретной оценки величины m1, определяющей скорость сходимости, проще всего пользоваться формулой: М1 = max½j‘(x)½, где max берется по отрезкуизоляции корня [а: b].
