Содержательная постановка задачи

Проведён эксперимент по определению зависимости коэффициента активности от ионной силы раствора.

Для этих величин необходимо рассчитать все характеристики случайных величин. Сделать вывод о наличии или отсутствии линейной зависимости

№	Ионная сила раствора Х(i)	Коэффициент активности Y(i)
	0,001 0,002 0,005 0,01 0,04 0,05 0,1 0,2 0,3 0,4 0,5	0,98 0,97 0,95 0,92 0,9 0,84 0,81 0,8 0,81 0,82 0,84

Табличные значения коэффициента Стьюдента = 2.201

Таблица значений критерия Стьюдента

f	q
0.80	0.90	0.95	0.98	0.99	0.995	0.998	0.999
	3.0770	6.3130	12.7060	31.820	63.656	127.656	318.306	636.619
	1.8850	2.9200	4.3020	6.964	9.924	14.089	22.327	31.599
	1.6377	2.35340	3.182	4.540	5.840	7.458	10.214	12.924
	1.5332	2.13180	2.776	3.746	4.604	5.597	7.173	8.610
	1.4759	2.01500	2.570	3.649	4.0321	4.773	5.893	6.863
	1.4390	1.943	2.4460	3.1420	3.7070	4.316	5.2070	5.958
	1.4149	1.8946	2.3646	2.998	3.4995	4.2293	4.785	5.4079
	1.3968	1.8596	2.3060	2.8965	3.3554	3.832	4.5008	5.0413
	1.3830	1.8331	2.2622	2.8214	3.2498	3.6897	4.2968	4.780
	1.3720	1.8125	2.2281	2.7638	3.1693	3.5814	4.1437	4.5869
	1.363	1.795	2.201	2.718	3.105	3.496	4.024	4.437
	1.3562	1.7823	2.1788	2.6810	3.0845	3.4284	3.929	4.178
	1.3502	1.7709	2.1604	2.6503	3.1123	3.3725	3.852	4.220
	1.3450	1.7613	2.1448	2.6245	2.976	3.3257	3.787	4.140
	1.3406	1.7530	2.1314	2.6025	2.9467	3.2860	3.732	4.072
	1.3360	1.7450	2.1190	2.5830	2.9200	3.2520	3.6860	4.0150
	1.3334	1.7396	2.1098	2.5668	2.8982	3.2224	3.6458	3.965
	1.3304	1.7341	2.1009	2.5514	2.8784	3.1966	3.6105	3.9216

Значения критерия Стьюдента (t-критерия) для различного уровня значимости q и числа степеней свободы f (f = n-2 или n, n-число опытов).

1. Математическое ожидание: 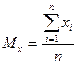и

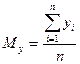
2. Дисперсия: 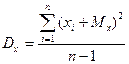и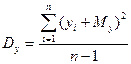

3. Среднее квадратическое отклонение: 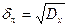и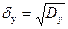

4 Коэффициент вариаци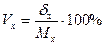и: и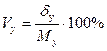

5. Нормированное отклонение: 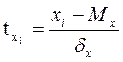и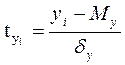

6. Коэффициент корреляции: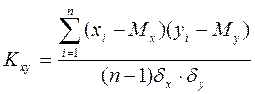

7. Критерий Стьюдента: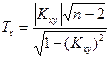

БЛОК-СХЕМА

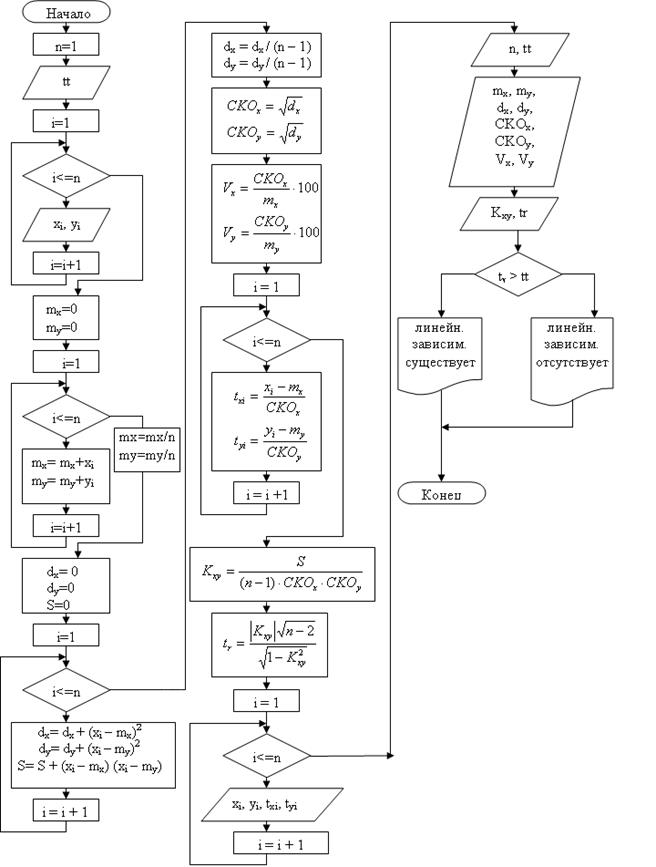
ПРОГРАММА НА ЯЗЫКЕ QBASIC

CLS

n = 11

INPUT "Введите Коэффициент Стьюдента="; tt

DIM x(1 TO n), y(1 TO n), tx(1 TO n), ty(1 TO n)

DATA 0.001, 0.002, 0.005, 0.01, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5

FOR i = 1 TO n

READ x(i)

NEXT i

DATA 0.98, 0.97, 0.95, 0.92, 0.9, 0.84, 0.81, 0.8, 0.8, 0.81, 0.82, 0.84

FOR i = 1 TO n

READ y(i)

NEXT i

mx = 0: my = 0

FOR i = 1 TO n

mx = mx + x(i)

my = my + y(i)

NEXT i

mx = mx / n: my = my / n

dx = 0: dy = 0: S = 0

FOR i = 1 TO n

dx = dx + (x(i) - mx) ^ 2

dy = dy + (y(i) - my) ^ 2

S = S + (x(i) - mx) * (y(i) - my)

NEXT i

dx = dx / (n - 1): dy = dy / (n - 1)

CKOx = SQR(dx): CKOy = SQR(dy)

Vx = CKOx * 100 / mx: Vy = CKOy * 100 / my

FOR i = 1 TO n

tx(i) = (x(i) - mx) / CKOx

ty(i) = (y(i) - my) / CKOy

NEXT i

Kxy = S / ((n - 1) * CKOx * CKOy)

tr = ABS(Kxy) * SQR(n - 2) / SQR(1 - Kxy ^ 2)

PRINT " N", "x", "y", "tx", "ty"

FOR i = 1 TO n

PRINT i, x(i), y(i), tx(i), ty(i)

NEXT i

PRINT "число ответов ="; n

PRINT "табличное значение критерия Стьюдента ="; tt

PRINT "математическое ожидание :"; "по x="; mx, "по y="; my

PRINT "дисперсия :"; "по x="; dx, "по y="; dy

PRINT "среднеквадратическое отклонение :"; "по x="; CKOx, "по y="; CKOy

PRINT "коэффициент вариации :"; "по x="; Vx, "по y="; Vy

PRINT "коэффициент корреляции ="; Kxy

PRINT "рассчитанное значение критерия Стьюдента ="; tr

IF tr >= tt THEN

PRINT "линейная зависимость между x и y Cуществует"

ELSE

PRINT "линейная зависимость между x и y Отсутствует"

END IF

END

РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ

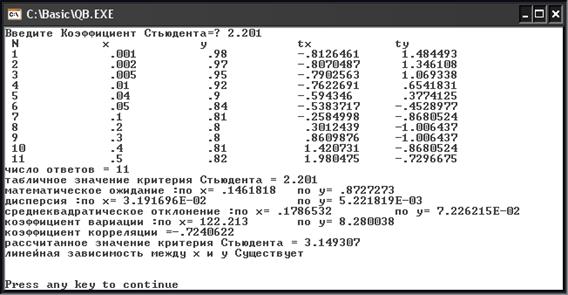
ПРИМЕР РАБОТЫ в EXCEL

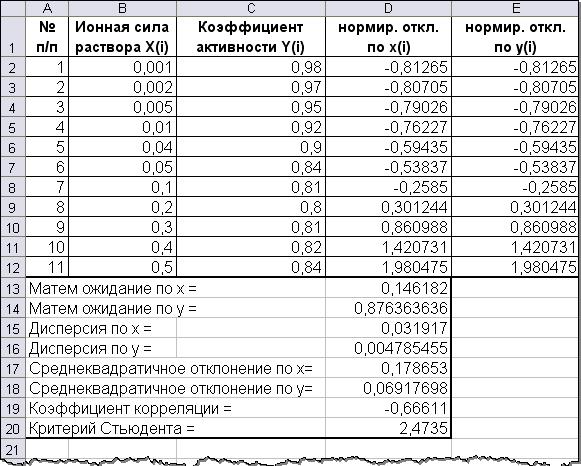
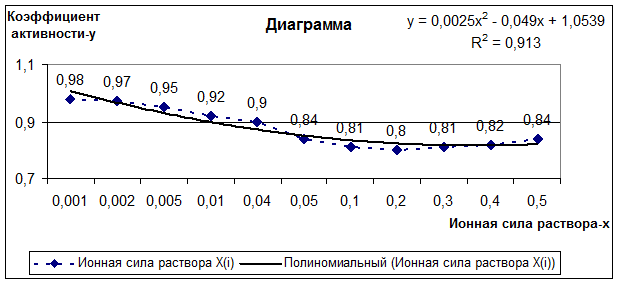
Результаты эксперимента

Контрольные вопросы

«Статистическая обработка результатов эксперимента»

1. Что характеризует математическое ожидание?

2. Какие характеристики оценивают разброс случайных величин?

3. Как определяется дисперсия?

4. Для чего необходим коэффициент вариации?

5. Как определить нормированное отклонение?

6. Что характеризует коэффициент корреляции?

7. В каких пределах измеряется коэффициент корреляции?

8. Как определить уровень значимости коэффициента корреляции?

9. Как выбирается Т_табл?

10. Какое соотношение должно быть между Т_расч и Т_табл, для утверждения, что линейная зависимость существует?

ЛАБОРАТОРНАЯ РАБОТА № 2
«Численное интегрирование»

Цель работы.

Ознакомится с принципом модульного программирования на примере задачи численного интегрирования. Использование оболочки QBASIC для построения процедур программ.