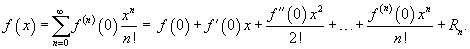Основные свойства определенного интеграла.

1) определенный интеграл – число, не зависящее от переменной интегрирования

2) константу можно вынести за знак интеграла

3) определенный интеграл суммы равен сумме интегралов в тех же приделах интегрирования

4) 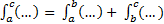– аддитивность

5) Интеграл от a до b равен отрицательному интегралу от b до a.

6)

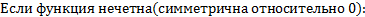
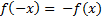
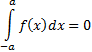
7)

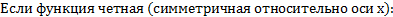
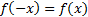
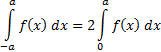
8)

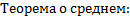
Если f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка с, что:

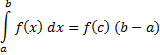
36. Способы вычисления определенного интеграла.

· Формула Ньютона-Лейбница:

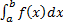= F(b) – F(a).

· Замена переменной.

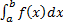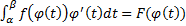= |^α_β = .

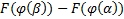37. Несобственные интегралы.

Суть: если промежуток интегрирования неограничен, то интеграл несобственный. Если при b, стремящемся к бесконечности, предел интеграла - конечное число, то такой интеграл – несобственный с бесконечным верхним пределом. То же самое с нижним пределом, но там минус бесконечность.

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен и непрерывная подынтегральная функция ограничена. Если хотя бы одно из этих условий не выполняется, приходится прибегать к понятию несобственного интеграла.

· Несобственные интегралы с бесконечными пределами.

Бесконечный верхний предел:

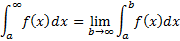
Если предел бесконечен или не существует, то несобственный интеграл не существует или расходится.

Бесконечный нижний предел:

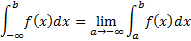
Два бесконечных предела:

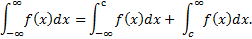
Вычисление несобственного интеграла:

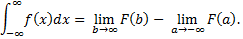
· Несобственные интегралы от разрывных функций.

Если f(x) определена и непрерывна на отрезке [a,b] за исключением точки c∈[a,b].

1) Разрыв в точке c=b – интеграл от функции с точкой разрыва на верхнем пределе.

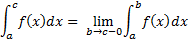
2) Разрыв в точке c=a – интеграл от функции с точкой разрыва на нижнем пределе.

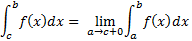
3) Разрыв во внутренней точке (a<c<b).

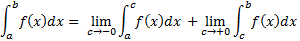
Функциональные ряды.

Функциональный ряд – ряд, членами которого являются функции от аргумента x:

u₁(x) + u₂(x) + u₃(x) + … + u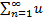_n(x) + … = _n(x).

Если зафиксировать x=x₀, то получим числовой ряд u₁(x₀) + u₂(x₀) + u₃(x₀) + … + u_n(x₀) + …

Если при x= x₀ числовой ряд сходится, то x₀ – точка сходимости функционального ряда.

Область сходимости – множество всех точек сходимости.

Сумма ряда в x= x₀: u₁(x₀) + u₂(x₀) + u₃(x₀) + … + u_n(x₀) + … = S(x₀).

Функциональный ряд 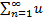_n(x) называется абсолютно сходящимся, если сходится ряд 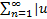_n(x)|.

Определение области сходимости:

· Признаки сравнения

· Признак Даламбера

· Признак Коши

39. Степенные ряды и их свойства.

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

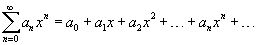
Часто рассматривается также ряд, расположенный по степеням (x − x₀), то есть ряд вида

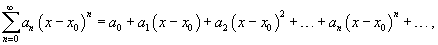
где x₀ − действительное число.

Свойства:

Рассмотрим степенной ряд

с₀ + с₁ х + с₂ х² + ... + с_{n x}ⁿ + ... , (10.1)

имеющий радиус сходимости R>0 (R может равняться 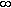). Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначим ее через S(x). Тогда можно записать равенство

S(x) = c₀ + c₁ x + c₂ x² + ... + c_n xⁿ + ... , (10.2)

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции S(x) в этой точке. В этом же смысле будем говорить, что ряд (10.1) сходится к функции S(x) на интервале сходимости. Вне интервала сходимости равенство (10.2) не имеет смысла.

Можно доказать, что сумма степенного ряда S(x) непрерывна и дифференцируема на любом отрезке [a, b] внутри интервала сходимости.

Равенство (10.2), справедливое в интервале сходимости степенного ряда, называют разложением S(x) в степенной ряд.

Для степенных рядов справедливы следующие утверждения:

Теорема 1.

Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S⁽ⁿ⁾(x).

Теорема 2.

Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если х (-R; R), причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны .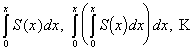

Теорема Абеля.

Если степенной ряд сходится при некотором x=x₀, где x₀ - число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что |x|<|x₀|. Наоборот, если ряд расходится при x=x0, то он расходится при всех значениях x таких, что |x|>|x₀|.

40. Область сходимости и радиус сходимости степенного ряда.

Радиус сходимости ряда – неотрицательное число R такое, что при |x|<R ряд сходится, а при |x|>R – расходится.

Интервал сходимости – (-R,R).

Найти R можно по признаку Даламбера (или признаку Коши).

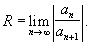
При x=±R ряд либо сходится, либо расходится (у каждого ряда по-своему).

Ряд Тейлора. Ряд Маклорена.

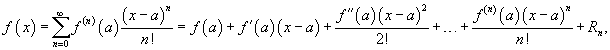
Если приведенное разложение сходится в некотором интервале x, т.е. 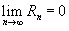, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Частный случай – ряд Маклорена (при a=0)