Аналитическое выражение второго закона термодинамики
Если изолированная система находится в неравновесном состоянии, то в ней всегда происходят самопроизвольные необратимые процессы, приближающие ее к состоянию равновесия.В конечном итоге система приходит в состояние равновесия, самопроизвольные необратимые процессы в ней прекращаются, а энтропия перестает увеличиваться, т.е. достигает своего максимума. Это означает, что условия равновесия системы могут быть выражены аналитически условиями максимума ее энтропии, т.е. соотношениями ds=0;
В связи с этими соображениями второй закон термодинамики может быть сформулирован так: энтропия неизолированной равновесной системы стремится к максимуму, достигая его, когда самопроизвольные процессы в ней прекращаются и система приходит в состояние равновесия.Эта формулировка показывает, что энтропия системы представляет собой параметр, изменение которого отражает не только качественные, но и количественные ограничения, накладываемые на тепловые процессы вторым законом термодинамики. В наиболее общей форме эти ограничения описываются формулой ds≥ которая и является, таким образом, аналитическим выражением второго закона термодинамики.
Применительно к неизолированным системам знак равенства показывает, что все процессы обмена энергией между системой и окружающей средой обратимы, а знак неравенства свидетельствует о наличии и необратимых процессов. Применительно к изолированным системам, для которых dq = 0 и, следовательно, аналитическое выражение второго закона термодинамики принимает вид ds ≥ 0, знак равенства показывает, что в системе необратимые процессы отсутствуют, а знак неравенства свидетельствует о наличии в ней необратимых процессов.Аналитическому выражению второго закона термодинамики можно придать вид: Tds≥dq
а поскольку по первому закону термодинамики dq=du+dl
любой термодинамический процесс должен удовлетворять соотношению Tds≥du+dl
которое является, таким образом, объединенным аналитическим выражением первого и второго закона термодинамики. Как ясно из предыдущего, знак равенства относится к обратимым процессам, а знак неравенства – к необратимым.
Внутренняя энергия реальных газов и их сжимаемость.
Между молекулами реальных газов действуют силы взаимного притяжения и силы отталкивания. При очень малых расстояниях преобладают силы отталкивания, а с увеличением расстояний начинают преобладать силы притяжения. Поэтому молекулы реального газа обладают внутренней потенциальной энергией. Внутренняя потенциальная энергия реальных газов зависит от среднего расстояния между молекулами, и в противоположность внутренней энергии реального газа, зависит также от удельного объема и давления. Внутренняя потенциальная энергия реальных газов может быть отрицательна, когда средние расстояния велики и преобладают силы притяжения и положительна с увеличением удельного объема.
Сжимаемость реальных газов – способность вещества изменять свой объем под действием всестороннего давления. Наличие у молекул реальных газов конечного по величине объема и сил притяжения между молекулами являются отличительными признаками реальных газов от идеальных, это влияние особенно четко сказывается на сжимании реального газа.
Термические коэффициенты.
Если известно уравнение состояния, то каждый параметр состояния может быть выражен как функция двух других параметров, т, е. 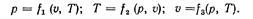
Полные дифференциалы этих величин будут:
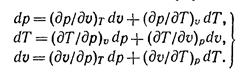
Частные производные при дифференциалах dp, dT и dv являются попарно величинами взаимно обратными и согласно правилам дифференциального исчисления между ними имеется следующая зависимость:
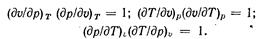
Следовательно, независимыми частными производными будут три из них. В качестве этих независимых производных выбирают следующие:
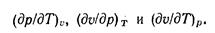
Эти частные производные входят в уравнение термических коэффициентов— сжатия, расширения и тепловой упругости, которые могут быть определены опытным путем.
Отношение частной производной (dV/dp) т к объему V характеризует скорость изменения объема с увеличением давления при постоянной температуре. Отношение называют изотермическим коэффициентом сжатия тела 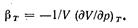 (4-9)
(4-9)
Знак минус в правой части равенства поставлен для того, чтобы рг получился положительной величиной, так как (dV/dp) т всегда отрицательна.
Отношение частной производной (dV/dT)p к объему V характеризует скорость изменения-объема при нагревании, если давление остается постоянным. Это отношение называют коэффициентом термического расширения тела 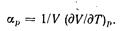 (4-10)
(4-10)
Отношение частной производной (др/дТ)у к давлению р характеризует интенсивность изменения давления при увеличении температуры, если объем тела остается постоянным.
Это отношение называют коэффициентом тепловой упругости «ли термическим коэффициентом давления 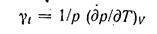 (4-11)
(4-11)
Уравнения Максвелла
