Представление синусоидальных величин вращающимися векторами

Любую синусоидально изменяющуюся величину, имеющую угловую частоту ω, можно изобразить вектором, вращающимся с постоянной угловой скоростью 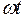против часовой стрелки, причем длина вектора в определенном масштабе равна амплитуде этой синусоидальной величины.

Рассмотрим вектор длиной А в прямоугольной системе координат (рис. 4.4).

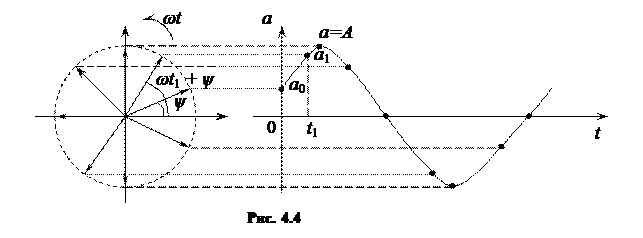Пусть в начальный момент времени t = 0 это вектор располагается под углом ψ к оси х, тогда его проекция на ось у будет равна некоторому значению а₀. Будем вращать этот вектор против часовой стрелки со скоростью ωt. Тогда в момент времени t₁ он повернется на угол ωt₁ + ψ, а его проекция на ось у будет равна а₁. В момент времени t₂ вектор повернется на угол ωt₂ + ψ, а его проекция на ось у будет равна а₂. Когда угол ωt + ψ достигнет значения 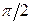, проекция вектора 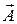будет максимальна и равна длине этого вектора.

При дальнейшем вращении проекция вектора будет уменьшаться, пока не достигнет нуля при ωt + ψ = π. Следующую половину окружности радиус-вектор опишет в области отрицательных значений у.

В результате за то время, когда радиус-вектор опишет полную окружность, его проекция на ось у опишет один период синусоиды. То есть при вращении радиуса-вектора изменение его проекции на ось ординат подчиняется синусоидальному закону, и один полный оборот радиуса-вектора соответствует одному периоду гармонического колебания. Аналитически это можно записать

.

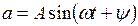Из этого следует, что значения проекций радиус-вектора в каждый момент времени соответствуют мгновенным значениям гармонически изменяющейся величины, а его длина равна амплитудному значению этой величины.

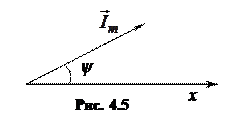Таким образом, при помощи радиуса-вектора можно описать любую синусоидальную величину. Если принять за длину вектора амплитуду тока, напряжения или ЭДС и вращать этот вектор с постоянной скоростью против часовой стрелки, то его проекции на ось ординат будут равны мгновенным значениям этих величин.

Тогда, например, ток 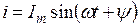можно изобразить вектором длиной I_m, который в момент времени t = 0 повернут относительно оси абсцисс на угол ψ (рис. 4.5).

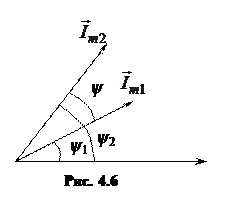Рассмотрим два тока:

;

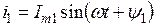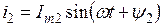
и изобразим их в виде векторов (рис. 4.6), вращающихся с одинаковой скоростью ωt. Если два вектора вращаются с одинаковой угловой скоростью, то при любых значениях фаз ψ₁ и ψ₂ в любой момент времени разность между ними остается постоянной

ψ = ψ₂ – ψ₁ = const,

то есть их взаимное расположение в пространстве остается неизменным.

Совокупность векторов, ориентированных друг относительно друга в пространстве определенным образом, называют векторной диаграммой.

Поскольку при работе электрической цепи все токи, напряжения и ЭДС в ней имеют одинаковую частоту, то их векторы будут вращаться с одинаковой скоростью, следовательно, в любой момент времени их взаимная ориентация в пространстве останется одинаковой. Исходя из этого, принято рассматривать не вращающиеся векторы, а неподвижные, учитывая их взаимную ориентацию в начальный момент времени (t = 0).

Изобразив токи или напряжения в виде векторов, длины которых равны амплитудным значениям, можно складывать или вычитать их по правилам сложения и вычитания векторов.

Для проведения математических действий над векторами необходимо построить их в определенном масштабе, так как надо помнить, что они выражают конкретные физические величины.

Пусть надо найти сумму двух токов:

;

.

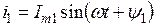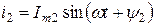Выбираем масштаб по току. Масштаб при построении векторных диаграмм записывается в виде числа, определяющего, сколько единиц тока приходится на один сантиметр:

,

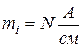где N – как правило, целое число. Обычно это число выбирают равным 1, 2, 5 или 10 (для малых токов допустимы масштабы, например, 0,1; 0,2; 0,5).

Находим длину отрезка 0А, соответствующего длине вектора 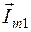, и длину отрезка 0В, соответствующего длине вектора 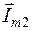, для этого делим амплитуды этих токов на масштаб:

, .

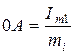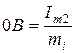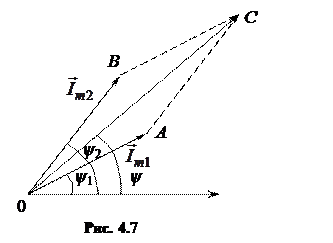Откладываем эти отрезки под углами ψ₁ и ψ₂, соответственно (рис. 4.7).

Следует помнить, что все векторы, над которыми производится вычисление, должны откладываться в одном и том же масштабе.

Для того чтобы сложить два вектора, строим параллелограмм, сторонами которого являются эти вектора. Диагональ параллелограмма, проведенная из точки 0, будет являться вектором суммарного тока. Для того чтобы найти амплитуду суммарного тока, измеряем эту диагональ и умножаем на масштаб .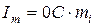

Начальную фазу тока находим, измеряя транспортиром угол наклона отрезка 0С к оси абсцисс. Записываем выражение для суммарного тока

.

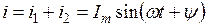В том случае, если складываются не два, а больше токов, удобнее пользоваться усеченным правилом параллелограмма – правилом треугольника, которое позволяет избежать лишних построений, загромождающих рисунок. Это правило проиллюстрировано на рис. 4.8.

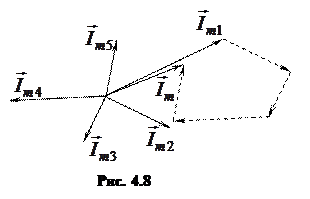Пусть требуется найти ток .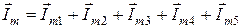

Тогда вектор тока 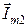параллельным переносом достраиваем к концу вектора 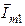, вектор тока 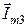переносим параллельно самому себе к концу вектора 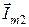и так далее. Начало первого вектора соединяем с концом последнего, это и будет вектор искомого тока.

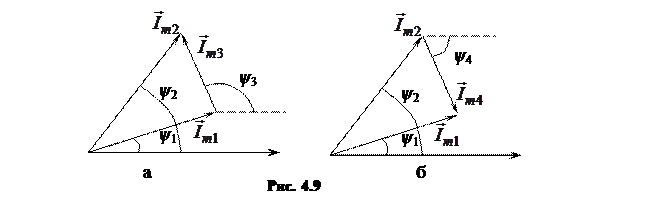Для того чтобы найти разность двух векторов, строим эти векторы в выбранном масштабе, соединяем концы векторов и ставим стрелку в сторону уменьшаемого (рис. 4.9).

Определение разности токов 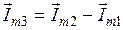показано на рис. 4.9, а, определение разности токов 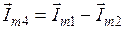– на рис 4.9, б. Из рисунков видно, что вектора 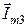и 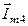имеют одинаковую величину, а разность их фаз 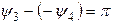составляет 180^о, то есть они находятся в противофазе.