Основные теоретические сведения

Дифференциальные уравнения

Основные теоретические сведения

Основные понятия теории дифференциальных уравнений 1-го порядка

Дифференциальным уравнением называется уравнение, связывающее между собой аргумент, функцию, ее производные: .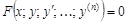

Порядок дифференциального уравнения равен порядку высшей производной, содержащейся в уравнении. Дифференциальное уравнение первого порядка .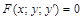

Решение (интеграл) − явная (неявная) функция 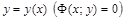, обращающая дифференциальное уравнение в тождество.

Общим решением (совокупность всех решений) − функция, которая удовлетворяет трем условиям:

1. содержит n произвольных постоянных величин, если n − порядок дифференциального уравнения;

2. при любых значениях произвольных постоянных является решением;

3. при произвольных начальных условиях позволяет решать задачу Коши (по заданным начальным условиям определить частное решение).

Решение уравнения 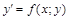существует в области X, где функция 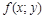непрерывна.

Геометрический смысл основных понятий

Дифференциальное уравнение первого порядка 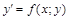геометрически представляет собой поле направлений касательных к интегральным кривым.

Общее решение − однопараметрическое семейство интегральных кривых 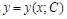, где C − параметр.

Решения, получающиеся из общего решения 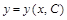при определенном значении произвольной постоянной C, называется частными.

График всякого решения 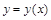данного дифференциального уравнения, построенный на плоскости 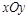, называется интегральной кривой этого уравнения.

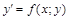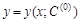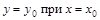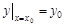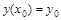Частное решение уравнения − интегральная кривая , угловые коэффициенты касательных к которой определяются данным дифференциальным уравнением. Задача нахождения частного решения, удовлетворяющего начальным условиям (другая запись или ), называется задачей Коши.

Пример. Пусть дано дифференциальное уравнение .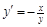

Что есть что?

1) Дифференциальное 2) Общее решение 3) Частное решение

уравнение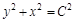

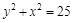
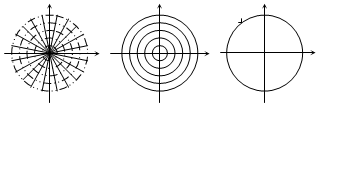у y у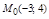

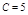
Интегральная кривая,

соответствующая начальному

условию .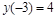

Рис. 10.

2. Рассмотрим методы нахождения решений дифференциальных уравнений 1-го порядка. Отметим, что общего метода нахождения решений не существует. Обычно рассматривают типы уравнений, и для каждого из них находят свой способ нахождения решения.

Уравнения с разделяющимися переменными. Уравнение вида

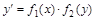, (6.1)

где, 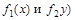− непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.

Для отыскания решения уравнения (6.1) нужно, как говорят, разделить в нем переменные. Для этого

1. заменим в (6.1) ,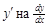

2. умножим обе части уравнения ,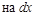

3. разделим обе части уравнения .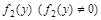

Тогда уравнение принимает вид

Тогда уравнение принимает вид

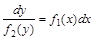. (6.2)

В этом уравнении переменная x входит только в правую часть уравнения, а переменная y − только в левую часть. Следовательно, переменные разделены. Далее необходимо проинтегрировать уравнение (6.2) и записать общий интеграл (решение).

Однородные дифференциальные уравнения. Функция 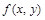называется однородной функцией измерения k относительно аргументов x и y если равенство 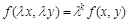справедливо для любого числа 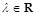, при котором функция 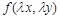определена, .

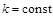Например, функция 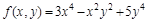является однородной четвертого измерения 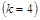, так как

.

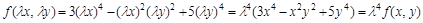Если 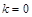, то функция будет однородной нулевого измерения, т.е.

.

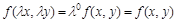Дифференциальное уравнение в нормальной форме

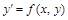(6.3)

называется однородным относительно переменных x и y, если 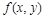- однородная функция нулевого измерения относительно своих аргументов.

Так как однородное дифференциальное уравнение (6.1) в нормальной форме всегда можно записать в виде 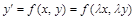, то, положив 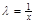, получим 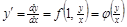. Следовательно, уравнение (6.3) с помощью замены 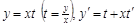сводится к уравнению с разделяющимися переменными относительно x и новой функции .

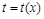Что необходимо для решения

Вариант контрольной работы

1. Найти общее решение дифференциальных уравнений:

а) 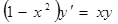;	в) ;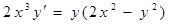
б) 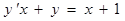;	г) .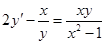

2. Найти общее решение дифференциального уравнения

а) 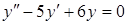, б) .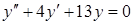

3. Определить и записать структуру частного решения 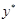линейного неоднородного дифференциального уравнения по виду функции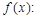

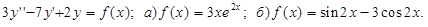
Дифференциальные уравнения

Основные теоретические сведения

Основные понятия теории дифференциальных уравнений 1-го порядка

Дифференциальным уравнением называется уравнение, связывающее между собой аргумент, функцию, ее производные: .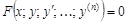

Порядок дифференциального уравнения равен порядку высшей производной, содержащейся в уравнении. Дифференциальное уравнение первого порядка .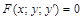

Решение (интеграл) − явная (неявная) функция 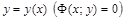, обращающая дифференциальное уравнение в тождество.

Общим решением (совокупность всех решений) − функция, которая удовлетворяет трем условиям:

1. содержит n произвольных постоянных величин, если n − порядок дифференциального уравнения;

2. при любых значениях произвольных постоянных является решением;

3. при произвольных начальных условиях позволяет решать задачу Коши (по заданным начальным условиям определить частное решение).

Решение уравнения 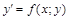существует в области X, где функция 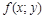непрерывна.