Проверочный расчет общей устойчивости стоек

Такая проверка требуется только при действии сжимающих продольных сил. Если силы приложены к центру сечения (М_х = M_y = 0), то снижение статической прочности стойки за счет потери устойчивости оценивают коэффициентом φзависящим от гибкости стойки.

Гибкость стойки, относительно материальной оси (т. е. оси, пересекающей элементы сечения) определяют по формуле

(20)

где l — длина полуволны изогнутой оси стойки, 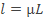. Коэффициент μ зависит от условий закрепления. Чем больше промежуточных закреплений, тем меньше гибкость при той же длине стойки L.У стойки, шарнирно закрепленной по концам (стойки Эйлepa), имеющей форму изгиба, близкую к полуволне синусоиды, μ = l. Для других схем закрепления также можно определить μ и l, рассматривая любую стойку как стойку, состоящую из стоек Эйлера или как часть стойки Эйлера. В случае консольного закрепления длина полуволны равна 2L и μ = 2.

Радиус инерции

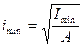
является характеристикой сечения и показывает, на какое расстояние в среднем удалены точки сечения стойки от оси возможного изгиба. Изгиб происходит в направлении наибольшей гибкости стойки, т. е. вокруг оси, относительно которой момент инерции наименьший. Если сечение состоит из четырех уголков, то по значению i_min близок к половине минимального габаритного размера поперечного сечения и почти не зависит от сечения уголка. Если сечение стойки составное и изгиб происходит относительно свободной оси, то за счет нежесткого соединения ветвей ее гибкость больше, чем полученная по формуле (20), поэтому используют приведенную гибкость

,

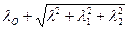где λ — гибкость, вычисленная по формуле (20). Если сечение состоит из двух ветвей и имеет только одну свободную ось, то 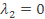. Если ветви соединены планками, то 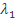— гибкость ветвей относительно оси 1 (см. рис. 2), параллельной оси изгиба и проходящей через центр сечения ветви (центральной оси ветви). Относительно оси 1 определяют радиус инерции ветви 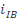при расчете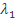

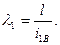
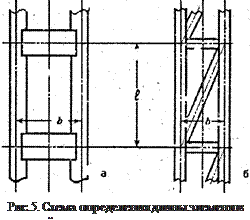
Длина l при этом равна расстоянию между серединами планок (рис. 5а).

Если ветви соединены решеткой (рис. 5б), то

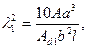
где А — сечение всей стойки; 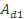- сечение раскоса лежащего в плоскости перпендикулярной оси 1; a — длина раскоса, b — расстояние между осями l двух ветвей.

Если сечение имеет четыре ветви и две свободных оси, то 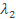определяют так же, как 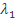, но относительно оси 2, проходящей через центр сечения ветви перпендикулярно оси изгиба.

Расстояние между планками l подбирают так, чтобы гибкость ветви была не более 40, т.е

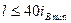
где i_Bmin— минимальный радиус инерции одной ветви.

При малой гибкости стойки (λ < 10) допускаемое напряжение близко к статической прочности материала [σ] → R_y, а φ → 1. При большой гибкости (λ > 100) допускаемое напряжение зависит только от одной характеристики материала — от модуля упругости. Так как все стали имеют примерно одинаковый модуль упругости, то допускаемое напряжение мало зависит от марки стали. Значит, применение высокопрочных сталей при большой гибкости сжатой стойки нерационально. Коэффициент φ учитывает это явление, и значения φ при большой гибкости таковы (табл. 72 приложения 6 СНиП), что произведение R_yφ при λ > 100 практически не зависит от R_y.Для стали ВСтЗсп ( 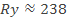МПа) φ можно определить по сокращенной табл. 6 как функцию только от наибольшей гибкости .

Таблица 6

λ	φ	λ	φ
	0,96		0,75
	0,93		0,69
	0,89		0,61
	0,85		0,54
	0,81		0,42

Как отмечено в п. 3, низкие значения φ свидетельствуют о нерациональном использовании металла. В связи с этим гибкость ограничивают. Для сжатых стоек она должна быть не выше 120.

После определения φ устойчивость стойки проверяют по формуле

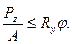(21)

Если стойка сжата внецентренно, то изгиб ослабляет устойчивость и значение φ снижается. Рассмотрим вначале изгиб относительно оси х (M_у=0) (см. рис. 1). Рационально подобранное сечение имеет наименьшую гибкость в плоскости действия момента. В связи с этим под действием изгибающего момента потеря устойчивости может произойти как в плоскости наименьшей гибкости, в которой действует момент М_х,так и в плоскости наибольшей гибкости. В любом случае устойчи­вость снижается с увеличением гибкости и относительного эксцентриситета т_х /см. формулу (1)/. Рассмотрим вначале потерю устойчивости в направлении наибольшей гибкости. При этой изгибно-крутильной форме потери устойчивости происходит закручивание стойки, и плоскость с наибольшей гибкостью поворачивается в направлении плоскости действия момента М_х. Расчет устойчивости проводят по формуле

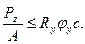(22)

Коэффициент φ_у определяют так же как при центральном сжатии, по табл. 6 в зависимости от гибкости стойки 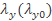при изгибе вокруг оси у. Коэффициент с учитывает уменьшение устойчивости от дёйствия момента М_x:

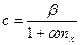. (23)

Коэффициент α для типов сечений, предложенных в задании, равен 0,6 при m_x 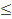1 и (0,55 + 0,05 т_x) при 1 < т_х ≤ 5: коэффициент β равен 1 при гибкости 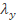< 100. Для других сечений и для 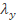> 100 следует определять α и β по табл. 10 СНиП [1].

Влияние изгиба в плоскости действия момента не удается свести к одному поправочному коэффициенту. Расчет проводят по формуле (21), а коэффициент φ_x определяют по более сложным таблицам, учитывающим одновременного влияние гибкости 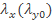в плоскости действия момента и относительного эксцентриситета m_x. Для ВСт.3сп и типов сечений, указанных в задании, значения φ можно найти по табл. 7, если х — материальная ось сечения, и по табл. 8, если х — свободная ось. Для других материалов, типов и соотношений размеров сечений следует определять φ по табл. 74 и 75 приложение 6 СНиП [1].

Таблица 7

λ	Значения φ при относительном эксцентриситете m
0,1	0,5	1,0	2,0	4,0	6,0	10,0	20,0
	0,95	0,76	0,60	0,42	0,28	0,20	0,12	0,05
	0,91	0,69	0,55	0,39	0,26	0,19	0,12	0,05
	0,86	0,64	0,51	0,36	0,24	0,18	0,11	0,05
	0,77	0,59	0,46	0,33	0,22	0,17	0,10	0,05
	0,67	0,53	0,41	0,30	0,20	0,15	0,10	0,04
	0,58	0,47	0,38	0,28	0,19	0,14	0,09	0,04
	0,49	0,42	0,34	0,25	0,17	0,13	0,09	0,04
	0,40	0,37	0,31	0,25	0,16	0,12	0,08	0,04
	0,34	0,32	0,26	0,20	0,14	0,11	0,07	0,04

Таблица 8

λ	Значение φ при относительном эксцентриситете m
0,1	0,5	1,0	2,0	4,0	6,0	10,0	20,0
	0,91	0,67	0,50	0,33	0,20	0,14	0,09	0,05
	0,87	0,64	0,48	0,33	0,20	0,14	0,09	0,05
	0,83	0,60	0,45	0,31	0,19	0,14	0,09	0,05
	0,77	0,56	0,42	0,29	0,18	0,13	0,09	0,05
	0,67	0,51	0,39	0,27	0,18	0,13	0,08	0,04
	0,58	0,46	0,35	0,25	0,17	0,12	0,08	0,04
	0,49	0,40	0,32	0,23	0,16	0,12	0,08	0,04
	0,40	0,35	0,29	0,21	0,15	0,11	0,08	0,04
	0,34	0,32	0,26	0,20	0,14	0,11	0,07	0,04

В случае изгиба в двух направлениях, когда в плоскости наибольшей жесткости действует момент M_x, а в другой плоскости — М_y, вначале проводят проверку устойчивости без учета М_y, а затем дополнительную проверку по формуле (21), подставляя коэффициент

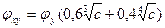. (24)

Значения 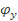определяют в зависимости от гибкости 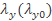и относительного эксцентриситета т_y по табл. 7, если ось у - материальная, или по табл. 8, если ось у – свободная. Коэффициент с находят по формуле (23). Таким образом, формула (24) учитывает влияние сразу двух изгибающих моментов 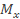и 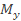.