Выбор типа поперечного сечения

ИСХОДНЫЕ ДАННЫЕ

Стержневая конструкция (см. рис. 1) одним концом жестко прикреплена к стенке, нагружена продольной силой Р_z и поперечной Q_y (x, y — главные оси поперечного сечения, z — продольная ось). Сила P_z приложена внецентренно, с эксцентриситетами e_x e_y (e_у > 0 при приложении силы Р ниже центра сечения). Значения силы P_z для разных вариантов задания приведены в табл.1, значения силы Q_y и эксцентриситетов — в табл. 2.

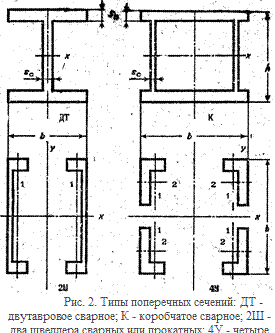
Предлагаемые типы поперечных сечений для разных вариантов задания представлены на рис. 2 и в табл.3. Поперечное сечение ограничено габаритами h_max и b_max , значения которых для двух подвариантов приведены в табл.4. Длина стержня L = 2 м. Материал — сталь ВСт.3сп.

Нагрузка циклическая, пульсирующая (с коэффициентом асимметрии цикла ρ = 0), число циклов за срок службы n = 10⁶. При работе на выносливость наибольшую концентрацию напряжений создают угловые швы, присоединяющие конструкцию к стенке (6-я группа по СНиП).

Максимальное поперечное перемещение свободного конца при расчете на жесткость .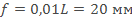

Таблица 1 Таблица 2

Варианты	Qy/Pz	ey, мм	ex, мм
1,4,7,10,13,16,19,22,25	0,4	-300
2,5,8,11,14,17,20,23,26	0,5
3,6,9,12,15,18,21,24,27

Вариант	Pz , кН
1…9
10…18
19…27

II. ЗАДАНИЯ

1-е задание

а. Построить эпюры изгибающих моментов и поперечных сил. Определить относительные эксцентриситеты приложенной нагрузки согласно СНиП и по их значениям установить, работает конструкция как балка или как стойка. В зависимости от этого выбрать тип поперечного сечения по табл. 3.

б. Подобрать размеры сечения, обеспечивающие прочность, устойчивость и жесткость конструкции при наименьшей массе. Определить массу конструкции, включая соединительные планки и ребра жесткости.

в. Подобрать размеры сечения с габаритами h_max и b_max, для подварианта А в 1,5 раза меньшими, а для подварианта Б в 1,5 раза большими, чем заданные в табл. 4. Сопоставить массу двух вариантов конструкции.

2-е задание

а. Спроектировать сварной узел, обеспечивающий прикрепление стержневой конструкции. Проверить прочность всех сварных швов.

Вариант	Тип сечения		Подвариант	hmax ,мм	bmax ,мм
стойки	балки
1…3, 10…12, 19…21	К	2Ш		А
4…6, 13…15, 22…24	4У	ДТ		Б
7…9, 16…18, 25…27	2Ш	К

б. Определить массу наплавленного металла.

в. Вычертить конструкцию в масштабе, в трех проекциях, с указанием размеров, с необходимыми разрезами и сечениями.

3-е задание

Определить перемещение свободного конца спроектированной конструкции от усадки сварных швов и от приложенных нагрузок.

III. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

Анализ расчетной схемы

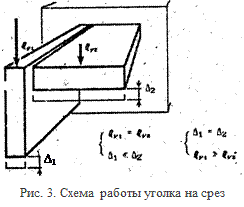Выбор сечения, обеспечивающего прочность и жесткость конструкций при минимальной массе, зависит от соотношения действующих на нее продольных и поперечных сил и моментов. При действии только продольной растягивающей силы P_z(см. рис. 1), приложенной по оси симметрии сечения, форма сечения может быть любой. Площадь сечения и масса конструкции, необходимые для обеспечения прочности, от формы сечения не зависят, так как напряжения по сечению распределены равномерно, и все части сечения одинаково участвуют в передаче, силы. При действии поперечной силы Q_y дело обстоит иначе. Рассмотрим стержень, выполненный в виде уголка из листовых элементов, один из которых обращен к линии действия силы Q_y ребром, а другой — плоскостью (рис.3). Жесткость этих элементов при сдвиге различна. При действии одинаковых касательных напряжений в сечении эле­мент, обращенный плоскостью к линии действия силы, прогнется сильнее, чем более жесткий, обращенный ребром к ней. Так как в действительности листовые элементы соединены между собой, образуют единое сечение и имеют одинаковый прогиб, то, следовательно, напряжения распределены неравномерно: основную часть силы Q_y воспринимает более жесткий элемент, в нем напряжения больше, и только от его сечения зависит прочность всей конструкции при работе на срез от силы Q_y.

При действии изгибающего момента важно не только, какие напряжения возникают в отдельных частях сечения, но и на каком расстоянии эти части сечения находятся от оси изгиба. Чембольше расстояние от оси, на котором находится некоторая часть сечения, тем больше плечо силы, передаваемой этой частью сечения и тем больше ее уча­стие в работе конструкции на изгиб. Однако сечение должно быть единым, поэтому нужен элемент, соединяющий части сечения, передающие изгибающий момент и разнесенные как можно дальше от оси. Примером наиболее эффективного сечения при изгибе является двутавр (см. рис. 2). Изгибающий момент передают полки двутавра, одна из которых растянута, а другая сжата. Стенка двутавра при чистом изгибе слабо нагружена, поэтому ее делают более тонкой, чем полки. При поперечном изгибе от действия силы Q_у (см. рис. 1) в сечениях возникают одновременно изгиб и срез. Изгиб воспринимают полки, а срез — стенка. Коробчатое сечение менее эффективно при изгибе, так как имеет две стенки, и, следовательно, его площадь больше. Однако оно эффективнее двутаврового при изгибе в двух направлениях вокруг осей х и у и при работе на кручение вокруг оси z.

Изгиб стержня возникает при действии поперечных сил, а также в случае внецентренного приложения продольной силы. При внецентренном растяжении деформация стержневой конструкции под нагрузкой приводит к уменьшению эксцентриситета, выпрямлению продольной оси стержня и приближению ее к линии действия силы. В случае сжатия эксцентриситет от искривления стержня увеличивается, что может вызвать потерю устойчивости всей конструкции или сжатых частей сечения, имеющих малую жесткость и сильно искривляющихся. Поскольку причиной потери устойчивости является изгиб, то меры для обеспечения устойчивости и жесткости те же, что и для обеспечения прочности при изгибе: части сечения должны быть разнесены как можно дальше от возможной оси изгиба. Это достигается при обеспечении общей устойчивости применением коробчатых и составных сечений, а при обеспечении местной устойчивости — усилением поперечными ребрами сжатых элементов сечения.

Приведенные соображения по выбору наилучшего сечения в зависимости от вида нагрузки показывают, что причины разрушения при растяжении, срезе, изгибе и сжатии различны, и объясняют, почему по СНиП для расчета одной и той же стержневой конструкции в этих случаях применяют разные формулы.

Растянутые стойки рассчитывают только на прочность, изогнутые и сжатые стойки— на прочность, жесткость и устойчивость. Как правило, действуют и продольная сила и изгибающий момент. В этом случае расчетную схему (стойки или балки) уточняют по относительному эксцентриситету, равному отношению напряжения от изгиба и напряжению от сжатия:

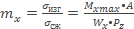, (1)

где A — площадь сечения, a W_x — момент сопротивления относительно оси х.

Для сплошного прямоугольного сечения

,

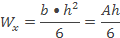для коробчатого или двутаврового сечения с толстыми полками и тонкими стежками

,

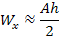для произвольного сечения

,

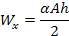где 0,33 ≤α<1. Чем выше α, тем лучше работает сечение на изгиб и устойчивость. Приняв
α ≈ 0,8, а h = h_max, можно по исходным данным найти т_х. Для определения M_{х maх} необходимо построить эпюру изгибающих моментов в стержне.

Аналогично рассчитывают относительный эксцентриситет т_у:

Если наибольший из относительных эксцентриситетов m_x и m_y имеет значение менее 0,1, то стойка по СНиП считается центрально сжатой (растянутой); если от 0,1 до 5 — внецентренно сжатой (растянутой); если т > 20, то стержневой элемент является изгибаемой балкой, растяжением и сжатием которой можно пренебречь; если т от 5 до 20, то растяжение или сжатие балки необходимо учитывать в расчете.

СПИСОК ЛИТЕРАТУРЫ

1. Строительные нормы и правила, Часть II. Гл. 23. Стальные конструкции
(СНиП II-23-81*) М.: НИТП Госстроя СССР, 1988. 96 с.

2. Николаев Г.А., Винокуров В.А. Сварные конструкции. Расчет и проектирование. М.: Высшая школа, 1990. 446 с.

3. Металлические конструкции. Общий курс. Учебник для вузов/Е.И. Беленя, В.А. Балдин, Г.С. Ведеников и др.; Под общ. ред. Е.И. Беленя. – 6-е изд., перераб. и доп. – М.: Стройиздат, 1986. – 560 с., ил.

ОГЛАВЛЕНИЕ

	Введение
I.	Исходные данные
II.	Задания
Ш.	Методика выполнения работы
1.	Анализ расчетной схемы
2.	Выбор типа поперечного сечения
3.	Определение размера сечения стойки
4.	Определение размера сечения балки.
5.	Проверочный расчет и» прочность
6.	Проверочный расчет общей устойчивости стоек
7.	Проверочный расчет общей устойчивости балки
8.	Проверочный расчет местной устойчивости элементов сечения
9.	Проектирование связей между ветвями составного сечения
10.	Проектирование прикрепления конструкции к стенке
11.	Определение прогиба стержневой конструкции
	Список литературы

ИСХОДНЫЕ ДАННЫЕ

Стержневая конструкция (см. рис. 1) одним концом жестко прикреплена к стенке, нагружена продольной силой Р_z и поперечной Q_y (x, y — главные оси поперечного сечения, z — продольная ось). Сила P_z приложена внецентренно, с эксцентриситетами e_x e_y (e_у > 0 при приложении силы Р ниже центра сечения). Значения силы P_z для разных вариантов задания приведены в табл.1, значения силы Q_y и эксцентриситетов — в табл. 2.

Предлагаемые типы поперечных сечений для разных вариантов задания представлены на рис. 2 и в табл.3. Поперечное сечение ограничено габаритами h_max и b_max , значения которых для двух подвариантов приведены в табл.4. Длина стержня L = 2 м. Материал — сталь ВСт.3сп.

Нагрузка циклическая, пульсирующая (с коэффициентом асимметрии цикла ρ = 0), число циклов за срок службы n = 10⁶. При работе на выносливость наибольшую концентрацию напряжений создают угловые швы, присоединяющие конструкцию к стенке (6-я группа по СНиП).

Максимальное поперечное перемещение свободного конца при расчете на жесткость .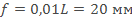

Таблица 1 Таблица 2

Варианты	Qy/Pz	ey, мм	ex, мм
1,4,7,10,13,16,19,22,25	0,4	-300
2,5,8,11,14,17,20,23,26	0,5
3,6,9,12,15,18,21,24,27

Вариант	Pz , кН
1…9
10…18
19…27

II. ЗАДАНИЯ

1-е задание

а. Построить эпюры изгибающих моментов и поперечных сил. Определить относительные эксцентриситеты приложенной нагрузки согласно СНиП и по их значениям установить, работает конструкция как балка или как стойка. В зависимости от этого выбрать тип поперечного сечения по табл. 3.

б. Подобрать размеры сечения, обеспечивающие прочность, устойчивость и жесткость конструкции при наименьшей массе. Определить массу конструкции, включая соединительные планки и ребра жесткости.

в. Подобрать размеры сечения с габаритами h_max и b_max, для подварианта А в 1,5 раза меньшими, а для подварианта Б в 1,5 раза большими, чем заданные в табл. 4. Сопоставить массу двух вариантов конструкции.

2-е задание

а. Спроектировать сварной узел, обеспечивающий прикрепление стержневой конструкции. Проверить прочность всех сварных швов.

Вариант	Тип сечения		Подвариант	hmax ,мм	bmax ,мм
стойки	балки
1…3, 10…12, 19…21	К	2Ш		А
4…6, 13…15, 22…24	4У	ДТ		Б
7…9, 16…18, 25…27	2Ш	К

б. Определить массу наплавленного металла.

в. Вычертить конструкцию в масштабе, в трех проекциях, с указанием размеров, с необходимыми разрезами и сечениями.

3-е задание

Определить перемещение свободного конца спроектированной конструкции от усадки сварных швов и от приложенных нагрузок.

III. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

Анализ расчетной схемы

Выбор сечения, обеспечивающего прочность и жесткость конструкций при минимальной массе, зависит от соотношения действующих на нее продольных и поперечных сил и моментов. При действии только продольной растягивающей силы P_z(см. рис. 1), приложенной по оси симметрии сечения, форма сечения может быть любой. Площадь сечения и масса конструкции, необходимые для обеспечения прочности, от формы сечения не зависят, так как напряжения по сечению распределены равномерно, и все части сечения одинаково участвуют в передаче, силы. При действии поперечной силы Q_y дело обстоит иначе. Рассмотрим стержень, выполненный в виде уголка из листовых элементов, один из которых обращен к линии действия силы Q_y ребром, а другой — плоскостью (рис.3). Жесткость этих элементов при сдвиге различна. При действии одинаковых касательных напряжений в сечении эле­мент, обращенный плоскостью к линии действия силы, прогнется сильнее, чем более жесткий, обращенный ребром к ней. Так как в действительности листовые элементы соединены между собой, образуют единое сечение и имеют одинаковый прогиб, то, следовательно, напряжения распределены неравномерно: основную часть силы Q_y воспринимает более жесткий элемент, в нем напряжения больше, и только от его сечения зависит прочность всей конструкции при работе на срез от силы Q_y.

При действии изгибающего момента важно не только, какие напряжения возникают в отдельных частях сечения, но и на каком расстоянии эти части сечения находятся от оси изгиба. Чембольше расстояние от оси, на котором находится некоторая часть сечения, тем больше плечо силы, передаваемой этой частью сечения и тем больше ее уча­стие в работе конструкции на изгиб. Однако сечение должно быть единым, поэтому нужен элемент, соединяющий части сечения, передающие изгибающий момент и разнесенные как можно дальше от оси. Примером наиболее эффективного сечения при изгибе является двутавр (см. рис. 2). Изгибающий момент передают полки двутавра, одна из которых растянута, а другая сжата. Стенка двутавра при чистом изгибе слабо нагружена, поэтому ее делают более тонкой, чем полки. При поперечном изгибе от действия силы Q_у (см. рис. 1) в сечениях возникают одновременно изгиб и срез. Изгиб воспринимают полки, а срез — стенка. Коробчатое сечение менее эффективно при изгибе, так как имеет две стенки, и, следовательно, его площадь больше. Однако оно эффективнее двутаврового при изгибе в двух направлениях вокруг осей х и у и при работе на кручение вокруг оси z.

Изгиб стержня возникает при действии поперечных сил, а также в случае внецентренного приложения продольной силы. При внецентренном растяжении деформация стержневой конструкции под нагрузкой приводит к уменьшению эксцентриситета, выпрямлению продольной оси стержня и приближению ее к линии действия силы. В случае сжатия эксцентриситет от искривления стержня увеличивается, что может вызвать потерю устойчивости всей конструкции или сжатых частей сечения, имеющих малую жесткость и сильно искривляющихся. Поскольку причиной потери устойчивости является изгиб, то меры для обеспечения устойчивости и жесткости те же, что и для обеспечения прочности при изгибе: части сечения должны быть разнесены как можно дальше от возможной оси изгиба. Это достигается при обеспечении общей устойчивости применением коробчатых и составных сечений, а при обеспечении местной устойчивости — усилением поперечными ребрами сжатых элементов сечения.

Приведенные соображения по выбору наилучшего сечения в зависимости от вида нагрузки показывают, что причины разрушения при растяжении, срезе, изгибе и сжатии различны, и объясняют, почему по СНиП для расчета одной и той же стержневой конструкции в этих случаях применяют разные формулы.

Растянутые стойки рассчитывают только на прочность, изогнутые и сжатые стойки— на прочность, жесткость и устойчивость. Как правило, действуют и продольная сила и изгибающий момент. В этом случае расчетную схему (стойки или балки) уточняют по относительному эксцентриситету, равному отношению напряжения от изгиба и напряжению от сжатия:

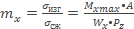, (1)

где A — площадь сечения, a W_x — момент сопротивления относительно оси х.

Для сплошного прямоугольного сечения

,

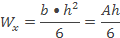для коробчатого или двутаврового сечения с толстыми полками и тонкими стежками

,

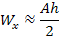для произвольного сечения

,

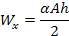где 0,33 ≤α<1. Чем выше α, тем лучше работает сечение на изгиб и устойчивость. Приняв
α ≈ 0,8, а h = h_max, можно по исходным данным найти т_х. Для определения M_{х maх} необходимо построить эпюру изгибающих моментов в стержне.

Аналогично рассчитывают относительный эксцентриситет т_у:

Если наибольший из относительных эксцентриситетов m_x и m_y имеет значение менее 0,1, то стойка по СНиП считается центрально сжатой (растянутой); если от 0,1 до 5 — внецентренно сжатой (растянутой); если т > 20, то стержневой элемент является изгибаемой балкой, растяжением и сжатием которой можно пренебречь; если т от 5 до 20, то растяжение или сжатие балки необходимо учитывать в расчете.

Выбор типа поперечного сечения

Для балок выбирают, как правило, сечение в виде двутавра (ДТ), двух швеллеров (2Ш) или коробчатое (К), (см. рис. 2), причем сечение располагают так, чтобы наибольший изгибающий момент действовал относительно оси х. Как отмечено в п. 1, двутавровое сечение имеет большую жесткость только относительно оси х, поэтому его следует применять, когда изгибающий момент М_у во много раз меньше, чем М_x . Такие же сечения применяют и для стоек, причем если сжатие стойки внецентренное (с изгибом), то сечение располагают так, чтобы изгиб происходил вокруг оси x (см. рис. 2). Но в большинстве случаев для стоек наиболее экономичными оказываются составные сечения из двух (2Ш) или четырех (4У) ветвей соединенных планками или решеткой из вспомогательных элементов. Увеличивая расстояния между ветвями, можно повысить жесткость сечения на изгиб без роста площади сечения. Однако при этом растут длина, сечение и масса вспомогательных элементов, соединяющих ветви, причем их суммарная масса может превысить массу ветвей сечения, особенно при значительной поперечной силе Q_y. Балки всегда имеют в сечении стенку, соединяющую полки, т. е. ось х у балки является материальной, а свободной может быть только ось у (ДТ, 2Ш, К на рис.2). Это связано с тем, что балки применяют при действии существенной поперечной силы Q_у и сосредоточенных поперечных сил (например, от тележки крана, перемещающейся по полке балки);

В исходных данных работы выбор типа сечения ограничен. Для каждого варианта предложен один тип сечения, если конструкция является стойкой, и другой — если она работает как балка (см. п. 1). Сечение следует расположить так, чтобы ось, обозначенная х на рис.2, совпадала с осью наибольшего изгибающего момента М_max, определяемого по эпюре. Расчет размеров сечения является весьма сложной операцией и в некоторых случаях осуществляется методом перебора: задают произвольные размеры сечения и проводят проверку конструкции на прочность и жесткость. Если прочность и жесткость не обеспечены, то увеличивают размеры сечения, а если обеспечены с большим запасом — уменьшают. Для сокращения числа попыток желательно подобрать сразу сечение, близкое к необходимому. Для этого при про­ектировании балок и стоек используют различные приемы.