Медиана: расчет для дискретных и интервальных вариационных рядов.

Медиана ( 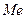) – значение признака у серединной единицы ранжированного вариационного ряда. Медиана делит вариационный ряд на две равные по числу единиц части.

Для определения данного показателя сначала рассчитывается порядковый номер медианы ( ):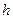

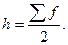
Далее по ряду накопленных частот определяется в дискретном вариационном ряду значение медианы, а в интервальном – медианный интервал. Определение медианного интервала позволяет рассчитать медиану в интервальном вариационном ряду по формуле:

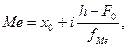
где 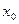– нижняя граница медианного интервала;

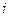– величина медианного интервала;

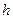– порядковый номер медианы;

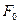– накопленная частота интервала, предшествующего медианному;

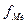– частота медианного интервала.

Графическое изображение вариационных рядов.

Анализ вариационных рядов распределения можно наглядно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, кумуляту и огиву распределения.

Полигон распределения используется для графического изображения дискретного вариационного ряда.

Гистограмма– столбиковая диаграмма, которую строят для графического изображения интервального вариационного ряда.

Кумулята представляет собой графическое изображение ряда накопленных частот.

Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получится огива.

Мода и медиана могут быть определены графически: мода в дискретном ряду – по полигону распределения, в интервальном ряду – по гистограмме; медиана – по кумуляте.

Понятие вариации признака, показатели вариации.

Для характеристики размера и интенсивности вариации изучаемого признака в совокупности используются показатели вариации:

Показатель вариации	Формула
простая	взвешенная
1. Размах вариации – разность между максимальным и минимальным значениями признака в совокупности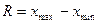
2. Среднее линейное отклонение показывает, насколько в среднем значение признака у каждой единицы совокупности отличается от среднего значения признака в совокупности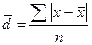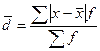
3. Среднее квадратическое отклонение показывает, насколько в среднем значение признака у каждой единицы совокупности отличается от среднего значения признака в совокупности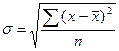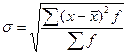
4. Дисперсия – квадрат среднего квадратического отклонения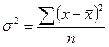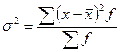
5. Коэффициент вариации – относительный показатель вариации, характеризующий степень однородности совокупности (совокупность считается количественно однородной, если коэффициент вариации не превышает 33%)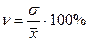

Расчет среднего квадратического отклонения и коэффициента вариации.

6. Среднее квадратическое отклонение показывает, насколько в среднем значение признака у каждой единицы совокупности отличается от среднего значения признака в совокупности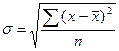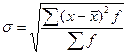