Вероятности некоторых нардовых событий.

Перейти к таблицам Вернуться в начало.

1. ВСТУПЛЕНИЕ

На нардовых сайтах часто спорят о вероятностях различных событий на нардовой доске. И самый первый тезис, с которым сталкиваешься и часто слышишь, звучит примерно так:

Последовательности 1234215 и 55554666 равновероятны и между ними нет никакой разницы. Все последовательности уникальны и у всех одинаковая вероятность выпадения.

Это утверждение верно.

Но неправильное его (утверждения) понимание ведет к большой путанице и многочисленным заблуждениям.

Приведу один ПРИМЕР.

Рассматривается вопрос: если 5 бросков подряд не выпадала четверка ни на одном заре, какова вероятность увидеть, хоть одну четверку в шестом броске?

Первый вариант ответа дают сторонники «уникальности всех последовательностей»:

Зары не имеют памяти, и не имеет значение, что выпадало до того. Вероятность увидеть четверку на одном из зар равна 11 из 36, 11/36 = 30,56%. Такая же вероятность будет, если до этого четверка не выпадала хоть 15 раз подряд!

Отметим, что на вопрос: какова вероятность увидеть хоть одну четверку в одном броске, ответ 11/36 совершенно верен. Но вопрос был про 6 бросков подряд, из которых в первых пяти четверки не было. А потому на заданный вопрос ответ 30,56% - неверен.

Второй вариант ответа звучит иначе:

Вероятность бросить одну четверку в одном броске зар действительно равна 11/36. Вероятность НЕ бросить ее равна 36/36 - 11/36 = 25/36. В последовательности из 6 бросков вероятность НЕ выбросить ни одной четверки, равна: (25/36)⁶ = 11,22%

Как видите, разница в 3 раза. А причина такого расхождения в том, что расчет вероятностей – очень деликатный и непростой вопрос. Он требует хорошего знания математики и очень корректной постановки вопроса.

«Нардовых» событий в длинных нардах может быть много, но мы рассмотрим только два случая:

- вероятность броска (бросков) зар;

- вероятность какого-то условия на броске (бросках) зар.

Короткие нарды мы не рассматриваем. Там есть еще дополнительная специфика вероятностей разных событий, связанная с боем шашек, выходом с бара и прочее.

Итак. В чем же специфика «нардовых» событий и почему позиция «уникальных последовательностей» приводит применительно к нардам к множеству ошибок?

1. СПЕЦИФИКА СОБЫТИЙ В ДЛИННЫХ НАРДАХ.

Никаких тайн, ни каких сложностей. На самом деле специфика «нардовых» событий, это всего лишь 2 пункта.

А) Бросок зар – это всегда две цифры от 1 до 6. Т.е. нардовые события это вероятности только парных сочетаний цифр от 1 до 6. Все остальное разнообразие многомерной комбинаторики нас не интересует, и мы будем рассматривать только парные броски зар.

Б) Для игры в длинные нарды, бросок 1:2 и 2:1 – это одно и то же. В отличие от нард, в комбинаторике 12 и 21 - две разные комбинации! Вот это и есть главное и критически важное отличие.

Весь дальнейший материал базируется на этой специфике.

1. ВЕРОЯТНОСТЬ БРОСКА ЗАР.

Вспомним классическую формулу вероятности события:

_{Количество благоприятных событий}

Вероятность какого-либо условия = ---------------------------------------------------------

^{Общее число всех возможных событий}

Начнем с одного броска зар. Это базовое, фундаментальное событие и знание вероятностей, связанных с одним броском необходимо для правильного восприятия игры длинные нарды.

Всего бросков зар может быть 6*6=36 вариантов, по 6 вариантов второго зара на каждую цифру первого зара (1-*, 2-*, 3-*, 4-*, 5-*, 6-*).

Разделим броски на два типа:

ОБЫЧНЫЙ бросок – цифры на зарах не равны, вероятность каждого конкретного такого броска равна 2 из 36, т.е. 2/36 или примерно 5,55%

Примеры:

- вероятность броска 4:5 равна 2 из 36, т.к. благоприятных событий два: бросок 4:5 и бросок 5:4, а всего возможных событий 36.

- вероятность броска 2:1 равна 2 из 36, т.к. благоприятных событий два: бросок 2:1 и бросок 1:2, а всего возможных событий 36.

- вероятность броска 4:6 равна 2 из 36, т.к. благоприятных событий два: бросок 4:6 и бросок 6:4, а всего возможных событий 36.

И т.д.

ПАРНЫЙ бросок илиКУШ – цифры на зарах равны, вероятность каждого конкретного такого броска равна 1 из 36, т.е. 1/36 или примерно 2,78%

Примеры:

- вероятность броска 5:5 равна 1 из 36, т.к. благоприятное событие всего одно: бросок 5:5, а всего возможных событий 36.

- вероятность броска 4:4 равна 1 из 36, т.к. благоприятное событие всего одно: бросок 4:4, а всего возможных событий 36.

- вероятность броска 1:1 равна 1 из 36, т.к. благоприятное событие всего одно: бросок 1:1, а всего возможных событий 36.

Ну и т.д.

ИТОГО. Вероятности:

Какого-либо конкретного обычного броска	2/36= 5,55%.
Какого-либо конкретного куша	1/36= 2,78%

1. ВЕРОЯТНОСТЬ КАКОГО-ТО УСЛОВИЯ НА БРОСКЕ (БРОСКАХ) ЗАР.

Здесь может быть много разных и в большинстве своем важных с точки зрения практической игры вероятностей.

Начнем по порядку.

А) Вероятность какого-нибудь (любого) куша, независимо какого именно:

Кушей всего 6 (1:1,2:2,3:3,4:4,5:5,6:6). Значит, вероятность равна 6/36=16,67%

Б) Вероятность обычного броска (НЕ КУШ), не зависимо от того, что именно выпадет на зарах. Вероятность, что бросок будет куш, как мы выяснили выше – 6 из 36, значит вероятность обычного броска равна 36/36-6/36=30/36=83,33% (100%-16,67%).

В) Вероятность, что в броске будет какая-то конкретная (как правило, очень нужная или наоборот очень не нужная) цифра, независимо от того, какая цифра вторая. Рассмотрим на примере вероятности выпадения хотя бы одной Четверки.

Всего бросков 36: 1-*, 2-*, 3-*, 4-*, 5-*, 6-*. В бросках 4-* - 6 благоприятных вариантов (4-1,4-2, 4-3, 4-4, 4-5, 4-6), каждом из остальных пяти бросков по одному (1-4,2-4, 3-4, 5-4, 6-4). Итого 11 вариантов из 36. Вероятность того, что в броске будет хотя бы одна Четверка = 11/36=30,56%. С остальными цифрами все точно так же.

Итак: вероятность броска какой-то конкретной цифры хотя бы на одном из зар равна 11/36или 30,56%

Г) Вероятность, что в броске НЕ будет какой-то конкретной (одной) цифры.

Как мы выяснили выше, вероятность, что хоть одна цифра выпадет, равна 11 из 36. Значит вероятность, что она НЕ выпадет, равна (36-11=25) из 36.

Итак: вероятность броска, в котором не будет какой-то конкретной цифры равна 25/36 или 69,44%

Это наиболее важные и постоянно применяемые в практике для расчетов в игре случаи.

Рассмотрим из остального многообразия еще несколько отдельных случаев.

ПРИМЕЧАНИЕ. Во избежание путаницы. В дальнейшем мы рассматриваем вероятности событий с шестеркой, но вероятности таких же событий с другими КОНКРЕТНЫМИ цифрами ровно такие же. Шестерка рассмотрена для примера.

a) Какова вероятность того, что ДВА броска подряд ни разу НЕ выпадет шестерка?

Вероятность НЕ выпадения шестерки в каждом броске равна 25/36. Значит, в двух бросках НЕ выпадение будет равно 25/36*25/36=625/1296=48,23%

b) Какова вероятность того, что в двух бросках подряд выпадет хотя бы одна шестерка?

Вероятность НЕ выпадения шестерки в 2 бросках подряд 48,23% (см. выше). Отсюда получаем, что вероятность выпадения хотя бы одной шестерки в хотя бы одном из двух подряд бросков равна 100%-48,23%=51,77%

c) Какова вероятность того, что N бросков подряд ни разу НЕ выпадет шестерка?

Вероятность НЕ выпадения шестерки в каждом броске равна 25/36. Значит, в N бросках НЕ выпадение будет равно (25/36)^ N

b) Какова вероятность того, что в N бросках подряд выпадет хотя бы одна шестерка? Вероятность НЕ выпадения шестерки хотя бы в одном из N бросков подряд равна (25/36)^ N, значит, вероятность выпадения равна 1-(25/36)^ N

Этот ответ будет правильным для любой конкретной цифры, например для четверки:

Количество подряд бросков N	Вероятность того, что, в каком-нибудь из N бросков подряд выпадет хотя бы одна шестерка (или любая другая конкретная цифра)	Вероятность того, что, N бросков подряд НЕ выпадет ни одна шестерка (или любая другая конкретная цифра)
	30,56%	69,44%
	51,77%	48,23%
	66,51%	33,49%
	76,74%	23,26%
	83,85%	16,15%
	88,78%	11,22%
	92,21%	7,79%
	94,59%	5,41%
	96,24%	3,76%
	97,39%	2,61%

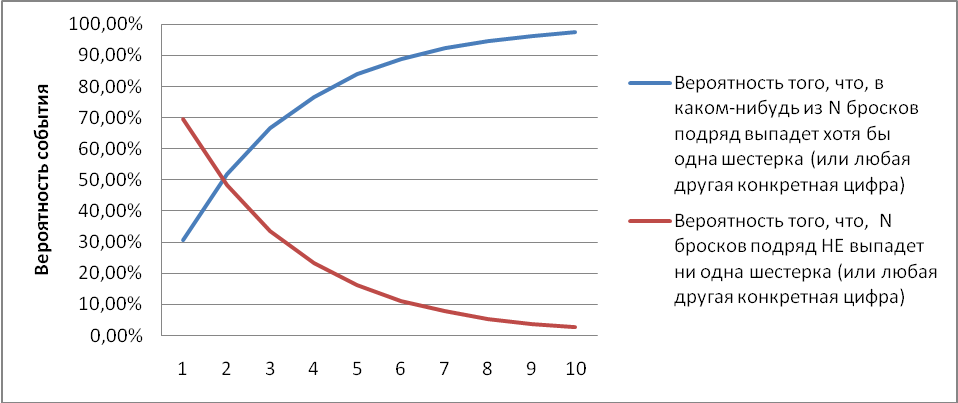
Еще несколько вероятностей, которые бывают нужны:

1. Какова вероятность, что выпадет 4 или 6 (хотя бы одна из двух цифр)?

Вероятность выпадения 4 равна 11 из 36, столько же для 6. Всего уже 22 из 36. Но считая варианты для 4, мы в т.ч. рассмотрели случаи 4-6 и 6-4, и то же самое сделали в расчете для 6. Значит, эти два случая посчитаны дважды. Вычитаем 2 из 22 и получаем ответ:

20/36или 55,56%

Этот ответ будет правильным для любых двух разных цифр на зарах.

2. Какова вероятность, что выпадет 2, 4 или 6 (хотя бы одна из трех цифр)?

Вероятность выпадения 4 равна 11 из 36, столько же для 6 и для 2. Всего уже 33 из 36. Дважды посчитанные варианты: 2-4, 4-2, 2-6, 6-2, 4-6, 6-2. Вычитаем 6 из 33 и получаем ответ: 27/36или 75,00%

Этот ответ будет правильным для любых трех разных цифр на зарах.

3. Какова вероятность, что выпадет два раза подряд один и тот же куш (например, 6:6)?

Вероятности в данном случае умножаются: (1/36)*(1/36)=(1/1296) или 0,077%

Вероятность бросить 3раза подряд 6:6 равна (1/36)*(1/36)*(1/36)=(1/45565) или 0,0021%

Вероятность бросить 4раза подряд 6:6 равна (1/36)*(1/36)*(1/36)*(1/36)=(1/1679616) или 0,00006%

Этот ответ будет правильным для любого конкретного куша.

4. Какова вероятность, что выпадет два раза подряд какой-нибудь куш (любой)?

Вероятности в данном случае умножаются: (1/6)*(1/6)=(1/36) или 2,77%

Вероятность бросить 3раза подряд какой-нибудь куш равна (1/6)*(1/6)*(1/6)=(1/216) или 0,46%

Вероятность бросить 4раза подряд какой-нибудь куш равна (1/6)*(1/6)*(1/6)*(1/6)=(1/1296) или 0,077%

5. Какова вероятность, что выпадет какой-нибудь (любой) куш хотя бы один раз из двух подряд бросков?

Вероятность, что не выпадет никакой куш, равна 5/6, что в двух подряд бросках не будет ни одного куша (5/6)*(5/6)=(25/36), значит, вероятность, что хоть раз выпадет, равна 1-(25/36)=(11/36) или 30,56%

Вероятность бросить хотя бы один раз какой-нибудь куш в одном из 3бросков подряд равна 1-(5/6)³ или 42,13%

Вероятность бросить хотя бы один раз какой-нибудь куш в одном из 4бросков подряд равна 1-(5/6)⁴ или 51,77%.

Вероятность бросить конкретный куш хотя бы раз из N бросков: 1 - (35/36) ^ N

Этот ответ будет правильным для любого конкретного куша.

СВОДНАЯ ТАБЛИЦА ВЕРОЯТНОСТЕЙ БАЗОВЫХ НАРДОВЫХ СОБЫТИЙ.

№	ВЕРОЯТНОСТЬ	Доли	%%
	Какой-либо конкретный куш	1 /3 6	2,78%
	Какой-либо конкретный обычный бросок	2 / 36	5,56%
	Какой-нибудь (любой) куш, не зависимо какой именно	6 / 36	16,67%
	Обычный бросок - НЕ КУШ, какой-нибудь	30 / 36	83,33%
	В броске будет какая-то конкретная цифра	11 / 36	30,56%
	В броске НЕ будет какой-то конкретной (одной) цифры	25 / 36	69,44%
	ДВА броска подряд ни разу НЕ выпадет конкретная цифра	625/1296	48,23%
	В двух бросках подряд выпадет хотя бы одна конкретная цифра	671/1296	51,77%
	Выпадет 4 или 6 (какая-то из двух заданных цифр)	20 / 36	55,56%
	Выпадет 2, 4 или 6 (какая-то из трех заданных цифр)	27 / 36	75,00%
	Выпадет два раза подряд один и тот же куш	(1/36)^2	0,07716%
	Выпадет три раза подряд один и тот же куш	(1/36)^3	0,00214%
	Выпадет четыре раза подряд один и тот же куш	(1/36)^4	0,00006%
	Выпадет два раза подряд какой-нибудь куш (любой)	(1/6)^2	2,78%
	Выпадет три раза подряд какой-нибудь куш (любой)	(1/6)^3	0,46%
	Выпадет четыре раза подряд какой-нибудь куш (любой)	(1/6)^4	0,07716%
	Выпадет какой-нибудь (любой) куш хотя бы один раз из двух подряд бросков?	1-(5/6)^2	30,56%
	Выпадет какой-нибудь (любой) куш хотя бы один раз из трех подряд бросков?	1-(5/6)^3	42,13%
	Выпадет какой-нибудь (любой) куш хотя бы один раз из четырех подряд бросков?	1-(5/6)^4	51,77%

Еще две интересные вероятностиот Олега (ник os2006, данные с форума fpclub ):

1. В партии, с количеством ходов N, вероятность получить К кушей (например, куша 66) имеет вид: N! / (N-K)! / K! * 35^(N - K) / 36^N. Для средней партии в длинные нарды получим таблицу и график ниже:

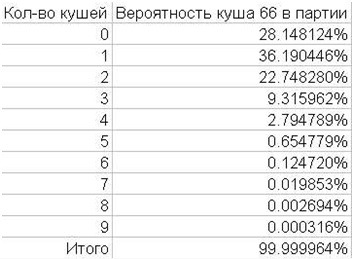
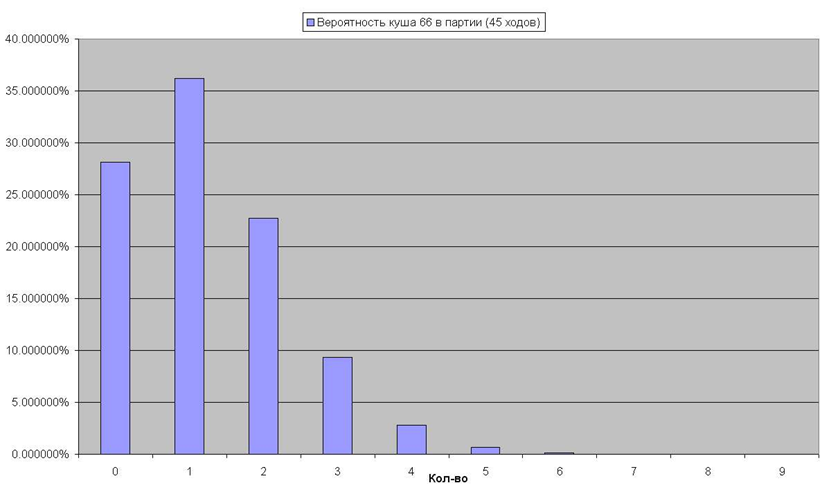
1. Также достойна внимания таблица:

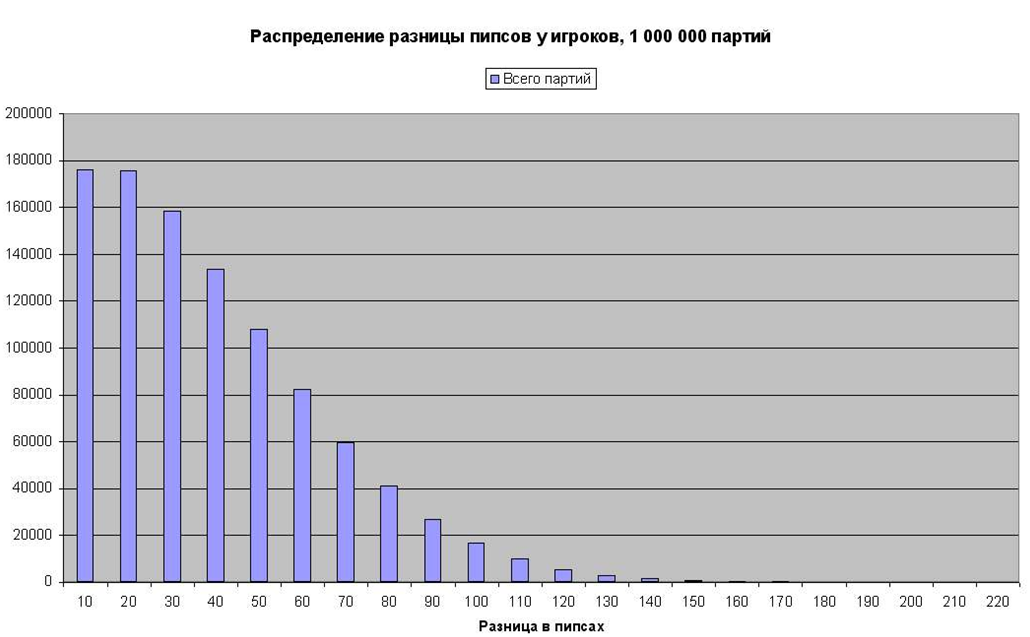
Как часто партия должна заканчиваться с разницей в пипсах всего 10 (в пределах 1 броска)? А с разницей 20 пипсов? Смотрите ниже таблицу и график.

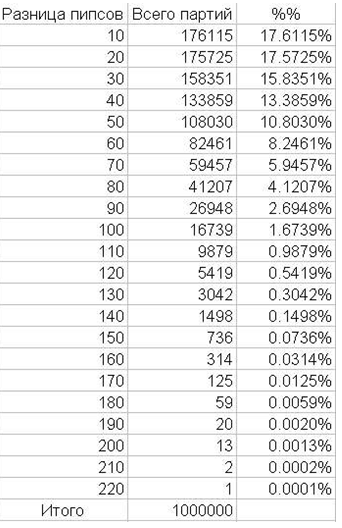
Пятая строка этой таблицы говорит о том, что каждая десятая партия должна заканчиваться с разницей в пипсах 50 очков. А первая строка должна вас приучить к тому, что примерно одинаково обоим игрокам (в пределах 10 пипсов разница) бывает только в каждой третьей партии. А в 2 из 3 партий разница будет больше.

Еще одна забавная цифра: если вы сыграете 200 партий, то 3 из них закончастя с разницей в пипсах около 100 очков.

Ну и, наконец, еще одна полезная таблица вероятностей.

Вероятность выбросить оставшиеся 2 шашки в самом конце игры:

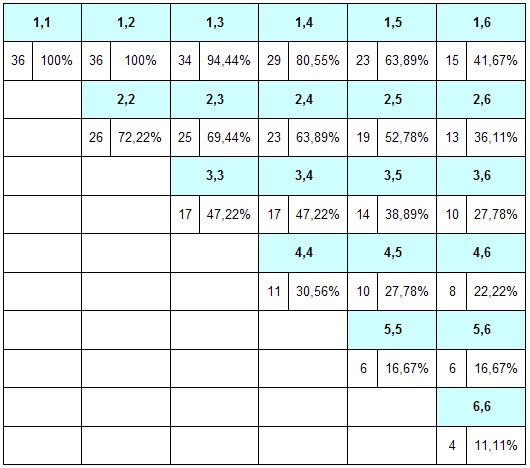
Для того, чтобы таблица стала понятнее, несколько картинок с шашками:

1,1 – две шашки на выброс в пункте 24 (последняя позиция доски для белых).

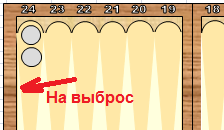
2,5 – одна шашка в пункте 23 (предпоследняя позиция) и одна в пункте 20.

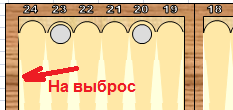
Взято с форума nardy.info.

НАРДОВАЯ ТОПОЛОГИЯ

Перейти к выводам. Вернуться в начало.

Движение шашек по нардовой доске имеет свою, ярко выраженную специфику и сильно отличается от законов движения тел, усвоенных нами еще со школы. Для тех, кто только начинает играть в нарды, очень важно обратить внимание на эту особенность. Она вызвана в основном несколькими факторами:

1. Длина пути шашки – конечная. Нардовая доска состоит из 24 пунктов, которые должна пройти каждая шашка, для того, чтобы выйти за пределы доски. Не забываем также, что по Правилам, шашка может встать лишь на тот пункт, который не занят шашкой соперника.

1. Движение шашек по нардовому полу дискретно. За один и тот же игровой темп (одно движение) шашка может передвигаться и на 1 пункт и на 6 пунктов.

В этом главная, фундаментальная особенность нардовой топологии: