Свободное и несвободное тело. Связи и их реакции. Принцип освобождаемости от связей. Основные виды связей.

Аксиомы статики

А1(1 з-н Ньютона) Аксиома инерции:

Тело сохраняет первоначальное состояние покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния.

А2 (3 з-н Ньютона) Аксиома взаимодействия:

Силы взаимодействия 2 тел равны по величине и направлены по одной прямой в противоположные стороны.

А3 Условия равновесия двух сил:

Для равновесия тела, находящегося под действием 2 сил, необходимо и достаточно, чтобы эти силы были равны по величине и направлены по одной прямой в противоположные стороны.

А4 Аксиома присоединения:

Система уравновешенных сил механического состояния твердого тела не изменит, если к нему присоединить или удалить систему уравновешенных сил.

А5 Аксиома параллелограмма:

Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложенных в этой же точке.

А6 Аксиома затвердевания:

Любое тело не изменит свое механическое состояние при переходе в абсолютно твердое.

Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Теорема о трех непараллельных силах.

Геометрическое условие равновесия:

Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого.

Аналитическое условие равновесия:

Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0).

Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0).

Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат.

Теорема о трех непараллельных силах:

Используется когда известны величина и направление одной силы, линия действия другой и точка приложения третьей.

Линии действия трех непараллельных уравновешенных сил, лежащих в одной плоскости, пересекаются в одной точке.

R12=F1+F2

Равновесие равнодействующей R12 сил F1 и F2 возможно только в том случае, если третья сила F3 будет направлена по линии действия R12 противоположно ей, т.е. проходить через точку пересечения линии действия сил F1 и F2.

Сложение параллельных сил.

Равнодействующая двух параллельных сил, направленных в одну сторону равна алгебраической сумме модулей составляющих сил. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Две параллельные, противоположно направленные силы, не равные по модулю, эквиваленты равнодействующей, модуль которой равен разности модулей слагаемых сил и направлены в сторону большей силы. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Если модули противоположно направленных сил равны, то такая система не имеет равнодействующей, она сообщает свободному телу вращательное движение и называется парой сил.

Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно точки.

Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (F x r). Получаем, что векторный момент силы относительно точки – векторная величина.

Связь между моментом силы относительно оси и векторным моментом силы относительно точки.

Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

Распределённые нагрузки.

Распределённые нагрузки:

Помимо сосредоточенных сил (приложенных в точке) встречаются случаи действия на тело нагрузок распределенных по объёму, поверхности или прямой линии. Такие нагрузки называются распределенными, и они характеризуются интенсивностью

q(кН/м;кН/м2;кН/м3). Распределённые нагрузки, как правило, заменяют сосредоточенными силами.

Распределённые нагрузки бывают двух видов:

равномерно распределённые (рисунок)

Q=qe

неравномерно распределённые (рисунок)

Q=1/2qe

Трение качения.

Трение качения

При решении задач обычно силы нормальной реакции прикладывают посередине площадки по которой происходит смятие, а трение качения учитывает пары сил с моментом трения, направленным противоположно возможному движению.

Аксиомы статики

А1(1 з-н Ньютона) Аксиома инерции:

Тело сохраняет первоначальное состояние покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния.

А2 (3 з-н Ньютона) Аксиома взаимодействия:

Силы взаимодействия 2 тел равны по величине и направлены по одной прямой в противоположные стороны.

А3 Условия равновесия двух сил:

Для равновесия тела, находящегося под действием 2 сил, необходимо и достаточно, чтобы эти силы были равны по величине и направлены по одной прямой в противоположные стороны.

А4 Аксиома присоединения:

Система уравновешенных сил механического состояния твердого тела не изменит, если к нему присоединить или удалить систему уравновешенных сил.

А5 Аксиома параллелограмма:

Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложенных в этой же точке.

А6 Аксиома затвердевания:

Любое тело не изменит свое механическое состояние при переходе в абсолютно твердое.

Свободное и несвободное тело. Связи и их реакции. Принцип освобождаемости от связей. Основные виды связей.

Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены.

В любом другом случае тело является несвободным.

Связи – ограничения, налагаемые на свободу любого несвободного тела.

Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Принцип освобождаемости от связей:

Всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их реакциями.

Виды связей:

ü Гладкая поверхность (опора без трения)

ü Шероховатая поверхность

ü Цилиндрический шарнир (подшипник)

ü Сферический шарнир

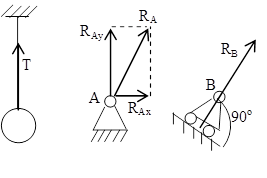
ü Гибкая нить

ü Невесомый стержень

ü Жесткая заделка (защемление)

ü Опорные реакции балок

Ø Шарнирно-подвижная опора

Ø 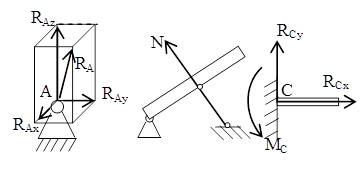Шарнирно-неподвижная опора

Ø 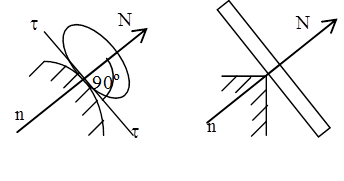Жесткая заделка

4) Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей.

Сходящимися называются силы, линии действия которых пересекаются в одной точке.

Если у такой системы сил л.д. расположены в одной плоскости, то она называется плоской системой сходящихся сил. В любом другом случае система сходящихся сил пространственная.

Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения 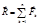. Равнодействующая может быть найдена геометрическим способом – построением силового (векторного) многоугольника или аналитическим способом, проектируя силы на оси координат.

Геометрический способ:

Теорема: любая система сходящихся сил приводится к равнодействующей, равной геометрической сумме составляющих сил и приложенных в точках пересечения линий их действия.

Сложность данного подхода в сложности геометрических построений.

Для упрощения построений сложим геометрически силы следующим образом: конец предыдущей силы должен совпадать с началом следующего, а л.д. сил должны быть параллельны заданным.

Замыкающая, полученная таким образом, и будет являться вектором равнодействующей, причем он должен быть направлен то начала к концу.

Аналитический способ:

Проекцией силы на ось называется направленный отрезок, заключенный между перпендикулярами, проведенными к соответствующей оси из начала к концу вектора силы.

В случае пространственной системы сил используется метод двойного проецирования: сначала сила проецируется на плоскость, а затем определяются проекции полученной проекции на осях координат.