Для выполнения лабораторных работ

По курсу СТАТИСТИКА

Для выполнения лабораторных работ

ПРЕДИСЛОВИЕ

Данные методические материалы по курсу «Статистика» предназначены для студентов всех форм обучения.

Курс «Статистика» позволяет обучающимся овладеть основами статистической методологии, а также элементарными навыками расчета и анализа экономических показателей.

Программа курса состоит из двух разделов: общей теории статистики и статистики в прикладных исследованиях.

Задания включают три раздела: - задания практических работ; - задания лабораторных работ; задания для самостоятельной исследовательской работы студента.

1. ЛАБОРАТОРНЫЕ РАБОТЫ

Выполнение лабораторных работ по статистике предполагает использование вычислительной техники и программных технологий для вычислений.

Правила оформления лабораторных работ:

Лабораторные работы выполняются согласно учебного плана. Ход и результаты работы должны быть оформлены в отдельной тетради в виде отчета.

Отчет должен содержать пункты:

1. Тема

2. Цель

3. Задание

4. План

5. Ход работы

6. Выводы

Объем отчета не должен превышать 1,5 – 2 листа.

Лабораторная работа №1

Тема: Правила построения таблиц

Цель работы: Получить навыки разработки таблиц.

План:

1. Разработка структуры таблицы.

2. Типы данных в таблице.

3. Запись формул в таблице.

4. Размещение таблиц в документе.

Задание: Разработать и построить таблицу начисления заработной платы по предприятию, используя исходные данные первой практической работы «Построение бизнес-плана нового предприятия».

Теоретический материал:

Для выполнения 1-2 пунктов рекомендуется использовать электронные таблицы Microsoft EXCEL для OFFICE 97,98,2000.

Структура таблицы:

- «Заголовок» таблицы полностью отражает ее содержание (цель исследования, место, время, основание, источник данных, главную единицу измерения); заголовок размещается по центру таблицы, без переносов и сокращений. Если текст заголовка получается громоздким, то можно дать ключевое определение, всю остальную информацию оформив комментарием внизу таблицы или сноской внизу текущего листа.

- «Шапка» таблицы состоит из колонок (столбцов, граф). Графы могут иметь простую и сложную структуру построения. Заголовки граф могут иметь переносы и сокращения по правилам русского языка, располагаются по центру клеток шапки. Заголовки простых либо главных клеток шапки пишутся с прописной буквы, заголовки подклеток – со строчной буквы. Для каждой колонки в шапке указывается единица измерения. Шапка является самым главным элементом построения таблицы. В первой графе размещается изучаемый показатель или подлежащее таблицы простого или сложного построения; как правило, подлежащее – это одна графа. Все остальные колонки – это сказуемое таблицы. Колонки сказуемого располагают в порядке:

1. результаты наблюдения (оперативная информация), группировки – эмпирические данные;

2. дополнительная информация для расчетов – данные априори;

3. расчеты по логике их выполнения.

Шапка таблицы вычерчивается полностью. Колонка с нумерацией строк не является обязательной и не входит в состав таблицы.

- «Строка Инициализации» содержит обозначение колонок таблицы. Подлежащее обозначается литерами (Заглавные буквы алфавита), колонки сказуемого нумеруются. В указанной строке допускается запись алгоритма расчетных колонок

- «Тело» таблицы содержит строки информации. Строки не вычерчиваются. Вертикально в теле таблицы проводятся основные конструктивные линии. При внесении эмпирических данных в таблицу, предусматриваются следующие правила:

1. если событие не произошло, то пишется слово «НЕТ»;

2. если данные отсутствуют, то ставится прочерк «-»;

3. если событие невозможно по логике вещей, то клетка перечеркивается Х.

Расчеты должны быть округлены: коэффициенты – до третьего знака после десятичной точки; проценты – до десятых; вычисляемые показатели – до сотых.

- «Сводка» – итоговая строка таблицы, ее результаты рассчитываются как суммы по соответствующим колонкам. Сводная строка вычерчивается.

Типы данных:

В электронных таблицах используем действительные, целые числа; текстовую информацию, даты – все эти типы устанавливаются через команду «ФОРМАТ» – «ЯЧЕЙКИ». Отображение данных на экране также может регулироваться кнопками панели инструментов «ФОРМАТИРОВАНИЕ»

Расчеты:

Алгоритм расчета начинается со знака «=» в ячейке, где мы ожидаем результат. Алгоритм ячейки представляет собой выражение, содержащее константы, имена переменных, имена встроенных и пользовательских функций, соединенных между собой математическими операциями и знаками приоритетов. Имена переменных представляют собой динамические и абсолютные адреса ячеек таблицы. Динамические адреса предполагают ссылку на текущие книгу, лист, строку и столбец. Абсолютные адреса фиксируют каждую ссылку знаком “$”. Встроенные функции вызываются ключевым словом и списком параметров в скобках, параметры функции разделяются «;». В качестве параметра может выступать другая функция

Размещение таблиц в документе:

В документе таблицы должны быть пронумерованы. Нумерация может быть сквозной или структурной. В сквозной нумерации проставляется порядковый номер таблицы в документе, в структурной указывается структурный номер раздела в документе и к нему добавляется текущий номер таблицы в данном разделе документа.

В разделе, где располагается таблица обязательно должна быть ссылка на нее.

Если к таблице идет обращение из нескольких разделов документа, то ее лучше поместить в приложение.

Если таблица не умещается на один лист, необходимо следить за тем, чтобы за шапкой следовало либо перед итогами располагалось не менее трех информационных строк.

Продолжение таблицы на новом листе оформляется сообщением о продолжении таблицы и переносом на новый лист строки инициализации.

Ссылки в таблице комментируются на том же листе, где они появились. Оформляются ссылки либо в нижнем колонтитуле, либо в специально выделенной строке внизу таблицы.

Таблица должна иметь внешнюю рамку по периметру, внутри таблицы размер шрифта допускается на разряд ниже, интервал строк в таблице одинарный.

Логические операции

Логические операции в электронных таблицах выполняются с помощью встроенной логической функции «ЕСЛИ» от трех аргументов.

Первый аргумент – логическое условие (>, <, =) в выражении.

Второй аргумент – алгоритм вычисления (формула) по ветке «ИСТИНА» логической операции.

Третий аргумент - алгоритм вычисления (формула) по ветке «ЛОЖЬ» логической операции.

Например:

Известно: - совокупный доход работника за месяц,

- количество льгот, необлагаемая сумма, тогда расчет подоходного налога должен быть выполнен по алгоритму:

1) «База для налога» = «доход» - «количество льгот» * «необлагаемая сумма»

2) Условие сравнения – «База для налога»>0

3) = ЕСЛИ(«База для налога»>0;округл(«база для налога»*0,13;0);0)

Расчет заработной платы

Данные для расчета взять и штатного расписания бизнес-плана предприятия, созданного вами на практических занятиях..

Внешние константы расчета: количество рабочих дней в месяце, необлагаемый налогом минимум.

1.1 Подлежащее таблицы: Реквизиты работника (табельный номер, ФИО).

2 Сказуемое.

2.1 Исходные данные:

- оклад;

- отработано дней;

- дней по больничному листу;

- % оплаты табличного листа;

- % премии;

- количество льгот подоходного налога;

2.2 Расчет

2.2.1 Начисления:

- начислено за рабочие дни;

- начислено за больничные дни;

- начислена премия;

- районный коэффициент;

- начислено итого

2.2.2 Удержания:

- удержан подоходный налог;

- удержаны перечисления;

- удержаны промежуточные выплаты;

- удержаны алименты;

- удержано итого.

2.2.3 Результат расчета (Сумма к получению).

Правила расчета:

1. Оплата повременная.

2. Премия начисляется только на отработанные дни.

3. Процент оплаты больничного листа: если непрерывный стаж работника меньше пяти лет, то процент оплаты – 0,6; если непрерывный стаж больше пяти лет и меньше восьми лет, то процент оплаты – 0,8; если непрерывный стаж больше восьми лет, то процент оплаты – 1.

Замечание 1: больничный лист по уходу за ребенком имеет более сложную дифференцированную систему коэффициентов.

4. Районный коэффициент начисляется на оплату рабочих и больничных дней, его величина в г.Бийске – 15% (или 0,15).

5. Если базовая сумма для начисления подоходного налога меньше 0, то подоходный налог не взимается.

Замечание 2. Здесь приведена упрощенная схема вычисления налога. В действительности налог удерживается не с ежемесячного начисления отдельно, а с совокупного дохода за год. Если совокупный доход превышает определенную границу, то подоходный налог удерживается в любом случае и ставка его увеличивается. Граница совокупного дохода достаточно высока, поэтому данное замечание в алгоритме учитывать не будем.

Лабораторная работа №2

Тема:Виды и формы статистического наблюдения

Цель: получить навыки работы по сбору и оформлению информации.

Задание:

1. Построить алгоритм расчета для полного списка работников.

2. Провести наблюдение. Заполнить таблицу.

3. Выполнить сортировку информации (по алфавиту сотрудников).

4. Построить сравнительную диаграмму окладов и итоговой суммы работников.

5. Составить пояснительную записку о выполненном расчете, приложить ведомость начисления.

Теоретический материал:

Для выполнения работы рекомендуется использовать электронные таблицы Microsoft EXCEL, Microsoft Word для OFFICE 97,98,2000 и созданную в предыдущей работе таблицу.

Расчет заработной платы является частью бухгалтерского учета предприятия, следовательно, – сплошным периодическим наблюдением. Начисление заработной платы происходит в определенный период месяца по штатному расписанию, приказу на начисление, данным отдела кадров, то есть имеет организованную форму. Устанавливаются критические сроки подачи сведений для расчета. Условия начисления заработной платы оговариваются в Уставе предприятия, бизнес-план которого вы разработали.

Сортировка.

Сортировка – это перестановка строк таблицы по возрастанию или убыванию признака (показателя), который в данный момент вы анализируете. Этот признак называется «Ключ сортировки».

Для перемещения информации в таблице в нужном ключе необходимо указать блоком строки целиком, подлежащие перемещению.

Если шапка таблицы простейшего построения (нет подколонок), то включите и ее в выбираемый блок таблицы, тогда при сортировке вам будут предложены ключи из названий шапки, - это очень удобно.

Если в шапке есть структурные колонки, то перед сортировкой добавьте в таблице после шапки пустую строку. Включите и ее в выбираемый блок таблицы, тогда при сортировке вам будут предложены ключи из литерных обозначений колонок, вам придется самим сопоставлять обозначения и названия показателей.

Выполнение сортировки возможно двумя способами: 1) с помощью кнопок на панели инструментов, но их ключ - только первая колонка выбранного блока; 2) через команду «Данные» - «СОРТИРОВКА» – самый грамотный вариант работы.

Замечание 2. Сортировка информации является очень рискованным мероприятием, поэтому перед началом такой работы сохраните таблицу, желательно и на дискету тоже, и дискету уберите в несгораемый сейф.

Диаграммы.

Для построения диаграмм необходимо решить для себя два ключевых вопроса:

- какие данные хотим иллюстрировать?

- Какая диаграмма для этого более всего подходит?

Колонки с исходными данными(оклад, отработано дней, дней по больничному листу) и промежуточными расчетами лучше всего изображать столбиковыми гистограммами, так как данная информация является первичной и дискретной.

Данные для диаграммы отмечаются блоком и вызывается «Мастер диаграмм».

Для правильного оформления необходимо пройти все этапы построения диаграммы. Если пунктов анализа много – более 30, то имеет смысл поместить диаграмму на отдельном листе расчетной книги, но не забывать об этом при печати.

Замечание 3. При построении столбиковых гистограммах важно помнить, что таблица и диаграмма обладают прямой и обратной связью: с одной стороны изменение исходных данных таблицы, влечет ее перерасчет и изменение внешнего вида иллюстрации; с другой – изменение величины столбиков рисунка вносит коррективу в исходные данные таблицы, меняет результат расчетов. Поэтому будьте осторожны при оформлении внешнего вида вашей диаграммы.

Для построения сравнительной диаграммы двух и более показателей (например сравнение оклада и суммы к получению) разрозненные колонки таблицы отмечаются сочетанием: клавиша CTRL и указатель мышки.

Пояснительная записка к расчету составляется в текстовом редакторе. Она содержит сообщение кем, когда и где выполнен расчет, на основании каких документов и распоряжений.

К пояснительной записке должна быть приложена ведомость начисления, содержащая графы:

- Табельный номер;

- ФИО;

- Сумма к получению;

- Подпись лица, получившего деньги в кассе.

Желаю успеха!

Лабораторная работа №3

Тема:Средние величины в статистике

Цель работы: получить навыки построения рядов распределения и расчета средних величин.

План:

1. Рассмотреть виды распределений.

2. Структурные средние величины.

3. Средние арифметические.

4. Средние гармонические.

5. Средние геометрические

6. Средние геометрические.

Задание:

1. Построить дискретный ряд распределения сотрудников предприятия по группам начисления, распределив сотрудников в группах по величине оклада. Провести полное исследование ряда. Рассчитать средний оклад по предприятию и по каждой группе. Снабдить расчеты иллюстрациями и комментариями.

2. Построить дискретный ряд распределения по возрастанию совокупного начисления сотрудникам предприятия, образовав пять равных интервалов. Провести полное исследование ряда. Рассчитать средний оклад по предприятию и по каждой группе. Снабдить расчеты иллюстрациями и комментариями.

Теоретический материал:

Для выполнения работы рекомендуется использовать электронные таблицы Microsoft EXCEL, Microsoft Word для OFFICE 97,98,2000 и созданную в предыдущей работе таблицу.

Группировка – разбиение элементов генеральной совокупности на основании главного изучаемого признака с дальнейшим объединением элементов в группы по тому же признаку.

Ряд распределения – это сгруппированная упорядоченная информация по главному изучаемому признаку.

Если подлежащее группировки – альтернативный признак, то ряд распределения – дискретный, иначе – если показатель непрерывный или множественный, то ряд распределения для него – интервальный.

Ряды распределения оформляются в таблице и иллюстрируются графиками.

Подлежащим ряда является группировочный признак, обозначается в расчетах переменной x_i,где i – счетчик групп, количество которых обозначим переменной целой n. Следующий показатель ряда – это количество элементов генеральной совокупности, попавших в ту или иную группу (частота), обозначим переменной f_i. Перечисленные выше показатели являются абсолютными статистическими величинами, так как выражаются в принятых единицах измерения.

Следующий показатель – это показатель структуры – доля (или частость) численности элементов каждой группы в общем объеме распределения. Если численность элементов каждой текущей группы - f_i, количество групп - n, общая численность элементов 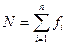, то доля текущей группы - 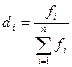- безразмерная величина, может быть выражена в долях. Тогда общее множество составляет 1, либо в процентах, тогда общее число элементов – 100%. Результаты долевых расчетов необходимо округлять очень аккуратно так, чтобы сумма всех долей равнялась точно единице. В большую сторону округлять имеет смысл наименьшие результаты, а в меньшую – наибольшие.

Структуру экономического процесса наилучшим образом иллюстрирует круговая диаграмма, где можно особо указать долю альтернативного признака.

Альтернативный признак – это совокупность значений изучаемого показателя, удовлетворяющих определенному условию либо вызывающих особый интерес у исследователя. Например, среди всех студентов, сдавших сессию с различными результатами, наибольший интерес у деканата вызывают студенты, сдавшие сессию на «хорошо» и «отлично».

Интенсивность нарастания элементов генеральной совокупности по нарастанию изучаемого признака показывает кумулята процесса – абсолютная статистическая величина, которая для каждой текущей группы рассчитывается как сумма всех предыдущих частот, включая частоту текущей группы. Кумулята – непрерывный показатель, потому ее изображают непрерывной ломаной линией.

Структурные средние величины распределения позволяют проанализировать его нормальность: чем ближе друг к другу мода, медиана и средняя арифметическая, тем ближе исследуемый ряд распределения к нормальному.

Мода – значение изучаемого признака в распределении с наивысшей частотой. Если наибольшую частоту имеют две и более группы, то распределение называется бимодальным.

Медиана – значение изучаемого признака, которое имеет средний по распределению элемент.

Средняя арифметическая величина - одна из разновидностей средних степенных, когда показатель степени равен единице. По генеральной совокупности в целом используется простая средняя арифметическая: 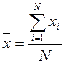. В дискретных рядах используется средняя арифметическая взвешенная: 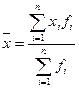. Перечисленные формулы используются, если информация представлена в явном виде.

Если известны обратные величины анализируемому показателю, то используется формула средней гармонической и средней гармонической взвешенной. Этот показатель рассчитывается из общей формулы средней степенной при показателе степени к=-1. Для генеральной совокупности в целом: ,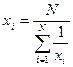

для дискретного ряда распределения - .

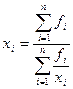В интервальных рядах распределения очень важно правильно выбрать количество интервалов. Для небольшой численности генеральной совокупности (N<200), число интервалов n должно находиться в диапазоне от 4 до 7. При N>200 полезно пользоваться формулой Стерджесса сглаженного роста числа интервалов относительно роста численности элементов исследования: n = 1 + 3,322LgN.

Длина интервалов может быть величиной постоянной, в этом случае ряд распределения равномерный. Пустые интервалы в распределении не допускаются, в случае такой ситуации выбирается новое число интервалов либо границы интервалов раздвигаются, и распределение становится неравномерным. В таблицу распределения кроме частоты добавляются колонки с длинами интервалов и их центрами.

Крайние интервалы могут быть неопределенными без четкой нижней или верхней границы. Параметры таких интервалов рассчитываются через определенные рядом стоящие.

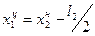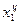Например, центр первого неопределенного интервала: , где - центр первого (младшего или нижнего интервала); 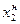- нижняя граница второго интервала, l₂ – длина второго интервала.

Для интервальных рядов распределения кроме частости рассчитывается плотность распределения как отношение частоты к длине интервала; плотность показывает концентрацию элементов совокупности по интервалам.

Замечание 1. По правилам умолчания интервалы распределения являются полуоткрытыми: нижняя граница включается в интервал, а верхняя – исключается. В процессе распределения единиц по интервалам, значение, попавшее на границу, относится к старшему (следующему) интервалу.

Замечание 2. Важно следить за тем, что бы критическое значение изучаемого признака выходило на границу интервала. Например, 100% выполнения плана должно быть нижней границей верхнего интервала.

Структурные средние величины рассчитываются по формулам:

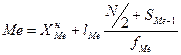, где S_Mе-1 – значение кумуляты на предыдущем перед медианным интервале.

.

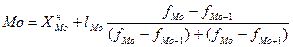Структурные средние величины могут быть найдены из графиков, но для этого очень важно подобрать масштаб и вычертить функции четко.

Средняя арифметическая в интервальных рядах рассчитывается через центры интервалов: 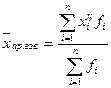; гармоническая взвешенная: .

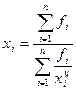Средняя геометрическая используется для усреднения относительных величин, таких как темпы роста, темпы прироста, индексы. Пример их вычислений рассмотрим в лабораторной работе №6.

Средняя квадратическая используется для оценки качества средней арифметической величины, и ее использование будет рассмотрено в следующей работе

Удачи в расчетах!

Лабораторная работа №4

Лабораторная работа №5.

Теоретический материал.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. Обычно это до 5 – 10%, реже до 15 – 25%. В основе выбора единиц для обследования положены принципы равных возможностей попадания в выборку каждой единицы генеральной совокупности. Это исключает тенденциозные ошибки и делает выборку репрезентативной.

Поскольку сама генеральная совокупность состоит из единиц с варьирующими признаками, то состав выборочной совокупности может в той или иной мере отличаться от состава генеральной. Это расхождение составляет ошибку выборки.

Применяя выборочный метод в экономических расчетах, обычно используют два основных вида обобщающих показателей: относительную величину альтернативного признака и среднюю величину количественного признака.

Для генеральной совокупности эти величины называются «генеральная средняя», (обозначается - 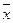) и генеральная доля (обозначается – р).

Для выборки – выборочная средняя (обозначается - 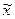), выборочная доля (обозначается - w). Выборочная доля или частость определяется из отношения числа выбранных единиц, обладающих изучаемым признаком, к численности выборки: .

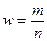Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки m. В математической статистике доказывается, что значения средней ошибки определяются по формулам: 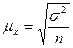- ошибка средней величины, 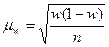- ошибка выборочной доли. Следует помнить, что отбор может быть повторным и бесповторным. Сущность повторного отбора состоит в том, что опрошенная единица после фиксации значения возвращается в генеральную совокупность и может быть опрошена снова. Вероятность быть опрошенной сохраняется постоянной у всех вариант.

При бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, вероятность быть опрошенными у оставшихся элементов возрастает, ошибки выборки уменьшаются на долю неопрошенных вариант. Ошибки бесповторного отбора рассчитываются по формулам:

, .

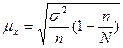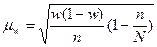Такие ошибки можно гарантировать не с абсолютной достоверность††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††. Вероятность суждения можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в t раз.

В практических экономических расчетах обычно ограничиваются значениями t, не превышающими двух-трех единиц. При этом выбор той или иной доверительной вероятности зависит от того, с какой степенью достоверности требуется гарантировать результаты выборочного обследования. Приведем часть таблицы распределения вероятностей:

Вероятность F(t)	0.000	0.0797	0.3829	0.6827	0.8664	0.9545	0.9876	0.9907	0.9973	0.99994
Кратность ошибки t	0.0	0.1	0.5	1.0	1.5	2.0	2.5	2.6	3.0

Предельные ошибки выборки рассчитываются по формулам:

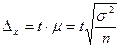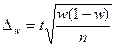, - - для повторного,

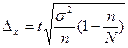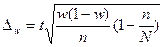, - для бесповторного отборов.

, .

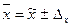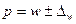Обратная задача выборочного наблюдения состоит в определении оптимальной численности выборки при условии, что заданы границы ошибок выборки и определен размер дисперсий. Формулы расчета численности студентам предлагается вывести самим.

Значения предельной ошибки и кратности ошибки определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки и наоборот. Вариация признака (дисперсия) существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно дисперсию определяют следующими способами:

1) берут из предыдущих исследований;

2) по правилу «трех сигм» общий размах вариации укладывается в 6 сигм (R @ 6s, отсюда s @ R/6). Для большей точности размах делят на 5;

3) Если хотя бы приблизительно известна средняя величина изучаемого признака, то s @ х_{ар.средн.}/3;

4) при изучении альтернативного признака, если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, берется максимально возможная величина дисперсии, равная 0,25.

При серийном отборе общее число отбираемых единиц делится на количество групп.

При стратифицированном отборе число наблюдений по каждой группе берется пропорционально структуре генеральной совокупности:

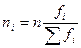, где n – численность выборки, n_i – число выбираемых элементов из одной подгруппы.

ЗАДАЧИ:

Задача 1.

На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.

Размер допустимой (предельной) ошибки – 1% или 0,01; принятая вероятность 0,95.

Задача 2.

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:

Месячный доход, руб.	600 - 1000	1000 - 1400	1400 – 1800	1800 – 2200
Число рабочих

Определить:

1) Среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997.

2) Долю рабочих предприятия, имеющих месячный доход 1400 руб. и выше, гарантируя результат с вероятностью 0,954.

3) Необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 50 руб.

По условию задачи известны:

При вероятности Р=0,954; t=2;

1) 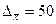руб.; s 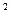=93184.

4) Необходимую численность выборки при определении доли рабочих с размером месячного дохода 1400 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

По условию задачи известны:

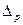=2%, или 0,02; при вероятности Р = 0,954; t = 2;

w=0,28.

Задача 3.

Операция шлифования при обработке детали № 312 производится в цехе на трех станках. Для определения процента брака для всей партии продукции, выработанной за день, проведено расслоение 10%-ной выборки. Отбор деталей из выработки каждого станка – случайный бесповторный; объем выработки пропорционален размеру выпуска. На первом станке было обработано 1700 деталей, на втором – 1000, на третьем –1800. Число забракованных деталей в выборке: по первому станку –2, по второму – 3, по третьему – 3.

Определить:

1) Доверительные интервалы, в которых с вероятностью 0,95 заключен процент брака для всей партии продукции.

2) Вероятность того, что процент брака для всей партии продукции отличается от полученного по выборке не более чем на 0,6%.

Для решения второго задания известна допустимая ошибка 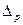=0,6%, или 0,006.

Задача 4.

При контрольной проверке качества апельсинов проведена 10%-ная серийная выборка. Из партии, содержащей 50 ящиков апельсинов (вес ящиков одинаков), методом механического отбора взято 5 ящиков. В результате сплошного обследования находящихся в ящике апельсинов получили данные об удельном весе бракованных апельсинов. Результаты следующие:

№ ящика, попавшего в выборку
Удельный вес бракованной продукции	1,2	1,8	2,0	1,0	1,5

Требуется с вероятностью 0,95 установить доверительные интервалы удельного веса бракованной продукции для всей партии апельсинов.

При вероятности Р=0,95; t = 1,96.

Задача 5.

Из партии электроламп произведена малая выборка (отбор случайный, бесповторный) для определения продолжительности службы ламп. Результаты выборки следующие:

№ лампы
Срок горения, час.

На основе приведенных данных требуется:

1) Определить доверительные интервалы, в которых заключена средняя продолжительность службы ламп для всей партии, гарантируя результат с вероятностью 0,99.

2) Определить вероятность того, что средний срок службы ламп для всей партии отличается от полученного по выборке не более чем на 40 часов.

Задача 6.

Обработка детали № 427производится в цехе на двух однотипных станках. При выборочном наблюдении (механический отбор единиц) были зарегистрированы следующие затраты на обработку одной детали:

Затраты времени на одну деталь, мин	Число деталей
Станок № 1	Станок № 2
1,5 - 2,5		-
2,5 - 3,5
3,5 - 4,5
4,5 - 5,5
Итого:

На основе приведенных данных определить, существенно ли расхождение в затратах времени на обработку одной детали для этих двух станков, гарантируя результат с вероятностью 0,95 [1,129].

Задача 7.

Из общего количества рабочих предприятия была проведена 30%-ная случайная бесповторная выборка с целью определения затрат времени на проезд к месту работы. Результаты выборки следующие:

Затраты врем. на проезд, мин.	До 30	30 - 40	40 - 50	50 - 60	60 – 70
Число рабочих

Определить: 1) средние затраты времени на проезд к месту работы у рабочих данного предприятия, гарантируя результат с вероятностью 0,997;

3) долю рабочих предприятия, у которых затраты времени на проезд к месту работы составляют 60 мин. И более, гарантируя результат с вероятностью 0,954.

Задача 8.

Выходной контроль качества поступающих на предприятие комплектующих изделий, осуществляемый в порядке механической выборки, дал результаты:

Отклонение размера изделия от принятого по ГОСТу, %	Число изделий
От -2,0 до -3,0 -1,0 до –2,0 0,0 до -1,0 1,0 до 0,0 2,0 до 1,0 3,0 до 2,0 4,0 до 3,0 5,0 до 4,0

Определить: 1) пределы значений среднего отклонения размера изделий от стандарта по ГОСТу с вероятностью 0,997;

3) пределы долей изделий с отрицательным отклонением в общей совокупности изделий с вероятностью 0,954.

Задача 9.

Произведен пропорциональный отбор рабочих со сдельной и повременной системами оплаты труда для изучения показателей выполнения сменного задания. Отбор единиц в каждой группе бесповторный. Выборка дала следующее распределение численности рабочих по проценту выполнения норм выработки:

Группы рабочих по оплате труда	Группы рабочих по проценту выполнения сменного задания	Итого рабочих
До 100	100-120	120-140	140 и выше
Рабочие – сдельщики
Рабочие – повременщики
Итого:

Определить:

1) Доверительные интервалы, в которых с вероятностью 0,954 заключен средний процент выполнения сменного задания для всех рабочих предприятия;

2) Возможные пределы доли рабочих, выполняющих сменное задание не менее чем на 120% (с вероятностью 0,954);

3) Необходимую численность выборки при определении доли рабочих, выполняющих сменное задание не менее чем на 120%, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 3%.

Задача 10.

В ООО «Прогресс» работает 3000 человек. Методом случайной бесповторной выборки обследовано 1000 человек, из которых 820 выполняли и перевыполняли дневную норму выработки.

Определить: 1) долю рабочих, не выполняющих норму выработки, по данным выборочного обследования;

2) долю всех рабочих акционерного общества, не выполняющих норму (с вероятностью 0,954).

Задача 11.

Из партии изготовленных изделий общим объемом 2000 единиц проверено посредством механической выборки 30% изделий, из которых бракованными оказались 12 изделий.

Определить:

1) долю бракованных изделий по данным выборки;

2) пределы, в которых находится процент бракованных изделий, для всей па