Тема: Системы линейных уравнений

Тема: Обратная матрица

Для матрицы 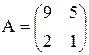обратная матрица 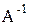имеет вид …

Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть
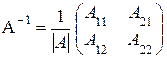– обратная матрица. Вычислим последовательно

,

,

,

,

.

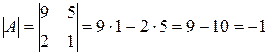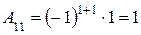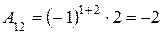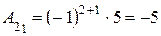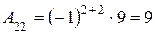Тогда .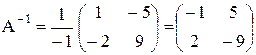

21. Тема: Обратная матрица
Для матрицы 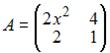не существует обратной, если значение x равно …

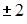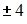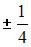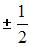Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

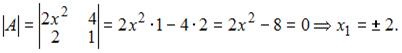
22. Тема: Обратная матрица
Для матрицы A существует обратная, если она равна …

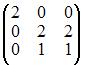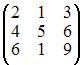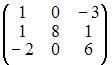Решение:
Всякая невырожденная квадратная матрица имеет обратную матрицу, то есть матрица имеет обратную, если определитель матрицы не равен нулю. Тогда вычислим определители 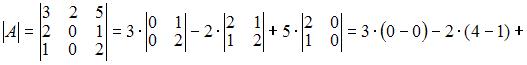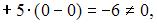то есть для матрицы 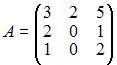существует обратная.
Так как определители остальных матриц равны нулю, то для них обратной матрицы не существует.

23. Тема: Обратная матрица
Для матрицы 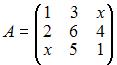не существует обратной, если значение x равно …

			– 2
			– 1

Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

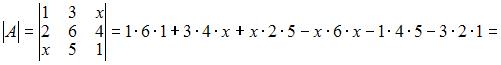
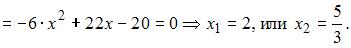
Тема: Обратная матрица
Для матрицы 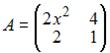не существует обратной, если значение x равно …

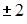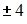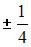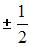Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

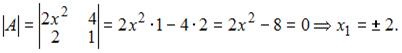
24. Тема: Обратная матрица
Для матрицы A существует обратная, если ее определитель …

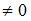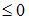			=0

Решение:
Для матрицы существует обратная, если определитель матрицы не равен нулю.

25. Тема: Обратная матрица

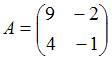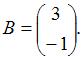Даны матрицы и Тогда решение матричного уравнения 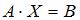имеет вид …

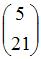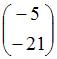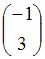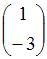Решение:
Решение матричного уравнения имеет вид 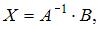где
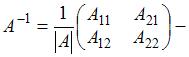обратная матрица.
Вычислим последовательно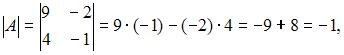




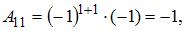
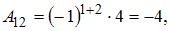
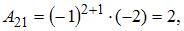
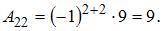
Тогда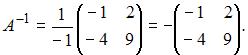
Следовательно,

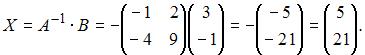
26. Тема: Обратная матрица

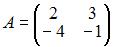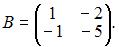Даны матрицы и Тогда решение матричного уравнения 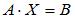имеет вид …

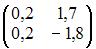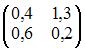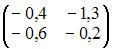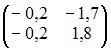Решение:
Решение матричного уравнения имеет вид: 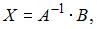где
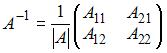– обратная матрица.
Вычислим последовательно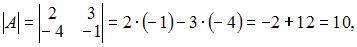




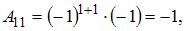
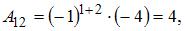
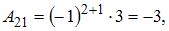
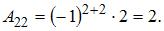
Тогда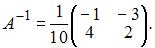
Следовательно,

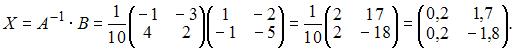
27. Тема: Обратная матрица

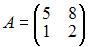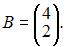Даны матрицы и Тогда решение матричного уравнения 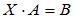имеет вид …

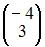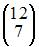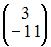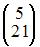Решение:
Решение матричного уравнения имеет вид 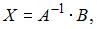где
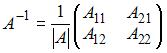– обратная матрица.
Вычислим последовательно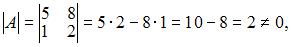




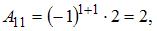
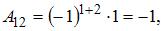
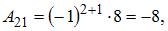
Тогда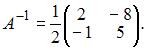
Следовательно,

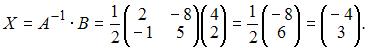
28. Тема: Обратная матрица

Для матрицы 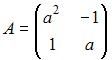существует обратная, если a равно …

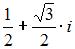			– 1

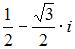Решение:
Матрица имеет обратную, если определитель матрицы не равен нулю, то есть 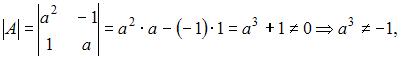тогда обратная матрица существует при 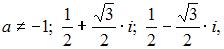например при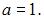

29.

29.
Тема: Обратная матрица

Дана матрица 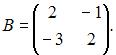Тогда обратной для матрицы 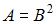является матрица …

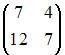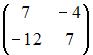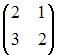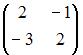Решение:
Вычислим 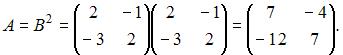Так как обратная матрица вычисляется по формуле 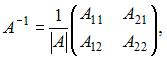то вычислим последовательно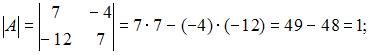


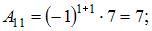
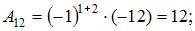
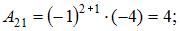
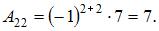
Тогда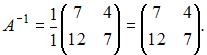

Тема: Ранг матрицы
Матрица, ранг которой равен единице, может иметь вид …

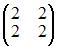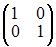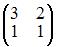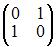Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Вычислим ранг каждой матрицы.
1) 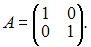Так как существует ненулевой минор второго порядка 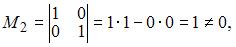то ранг матрицы равен двум.
2) 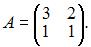Так как существует ненулевой минор второго порядка 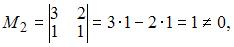то ранг матрицы равен двум.
3) 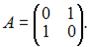Так как существует ненулевой минор второго порядка 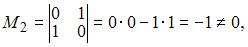то ранг матрицы равен двум.
4) 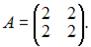Так как существует ненулевой минор первого порядка, например 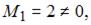а минор второго порядка 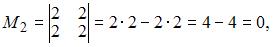то ранг матрицы равен единице.

Тема: Ранг матрицы
Ранг матрицы 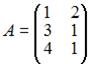равен …

Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Существуют ненулевые миноры второго порядка, например:

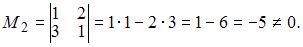
Следовательно, ранг равен двум.

30. Тема: Системы линейных уравнений
Методом Крамера не может быть решена система линейных уравнений …

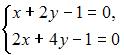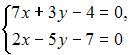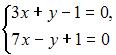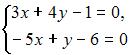Решение:
Систему линейных алгебраических уравнений можно решить методом Крамера, если ее определитель не равен нулю.
1. Из системы 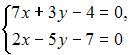получим 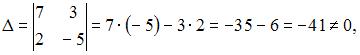следовательно, система может быть решена методом Крамера.
2. Из системы 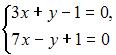, получим 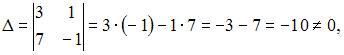следовательно, система может быть решена методом Крамера.
3. Из системы 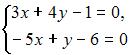получим 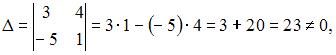следовательно, система может быть решена методом Крамера.
4. Из системы 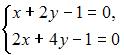получим 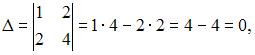следовательно, система не может быть решена методом Крамера.

31. Тема: Системы линейных уравнений

Методом Крамера не может быть решена система линейных уравнений …

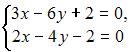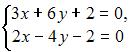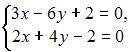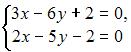Решение:
Систему линейных алгебраических уравнений можно решить методом Крамера, если ее определитель не равен нулю.
1. Из системы 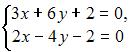получим 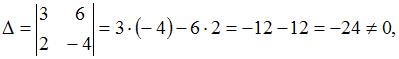следовательно, система может быть решена методом Крамера.
2. Из системы 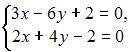получим 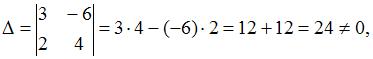следовательно, система может быть решена методом Крамера.
3. Из системы 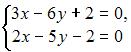получим 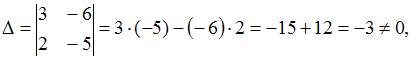следовательно, система может быть решена методом Крамера.
4. Из системы 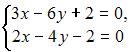получим 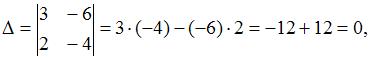следовательно, система не может быть решена методом Крамера.

32. Тема: Системы линейных уравнений

Задание 3 (

– выберите один вариант ответа).

Система линейных уравнений 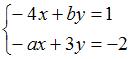имеет решение 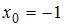, 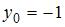при …

Варианты ответов:

• 1)
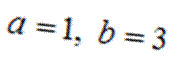
• 2)
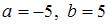
• 3)
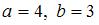
• 4)

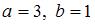
33. Тема: Системы линейных уравнений

Задание 3 (

– установите соответствие между элементами двух множеств).

Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1.
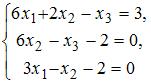
2.
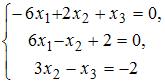
3.
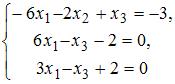
4.

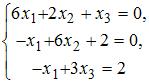
Варианты ответов:

• 1)
• 2)
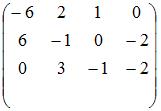
• 3)
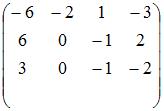
• 4)
• 5)

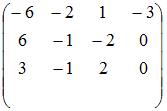
6)

34. Тема: Системы линейных уравнений
Матричным методом может быть решена система линейных уравнений …

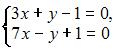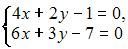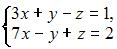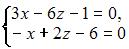Решение:
Систему линейных алгебраических уравнений можно решить матричным методом, если ее определитель не равен нулю.
1. Из системы 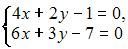получим 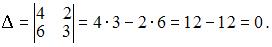Следовательно, система не может быть решена матричным методом.
2. Система 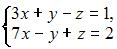не может быть решена матричным методом, так как количество переменных превышает число уравнений.
3. Из системы 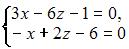получим 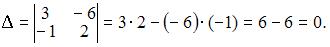Следовательно, система не может быть решена матричным методом.
4. Из системы 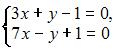получим 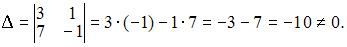Следовательно, система может быть решена матричным методом.

35. Тема: Системы линейных уравнений
Матричным методом не может быть решена система линейных уравнений …

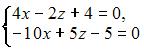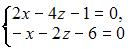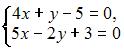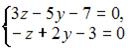Решение:
Систему линейных алгебраических уравнений можно решить матричным методом, если ее определитель не равен нулю.
1. Из системы 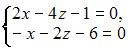получим 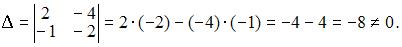Следовательно, система может быть решена матричным методом.
2. Из системы 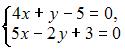получим 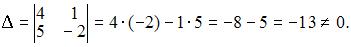Следовательно, система может быть решена матричным методом..
3. Из системы 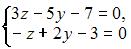получим 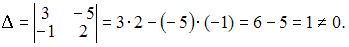Следовательно, система может быть решена матричным методом.
4. Из системы 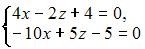получим 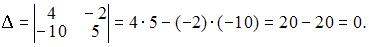Следовательно, система не может быть решена матричным методом.

Тема: Обратная матрица

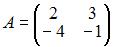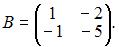Даны матрицы и Тогда решение матричного уравнения 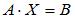имеет вид …

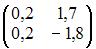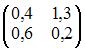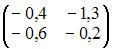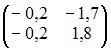Решение:
Решение матричного уравнения имеет вид: 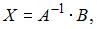где
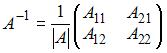– обратная матрица.
Вычислим последовательно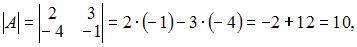




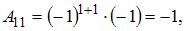
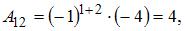
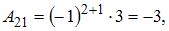
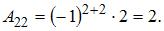
Тогда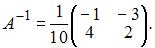
Следовательно,

36.

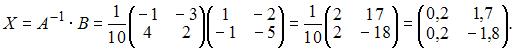
36.Тема: Системы линейных уравнений

Базисное решение системы 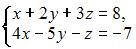может иметь вид …

			(2; 3; 0)
			(– 2; – 3; 0)
			(3; 2; 0)
			(– 3; – 2; 0)

Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
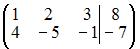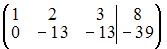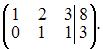~ ~ Следовательно, система может быть записана в виде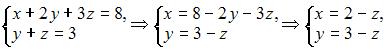
где 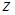– свободная переменная, а 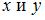– базисные. Общее решение будет иметь вид 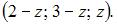Базисным решением называется всякое решение системы, в котором свободные переменные имеют нулевые значения. Значит,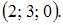

37.

37.
Тема: Системы линейных уравнений

Однородная система 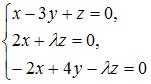имеет только одно нулевое решение, если 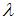принимает значения не равные …

			– 2
			– 1

Решение:
Система линейных однородных уравнений 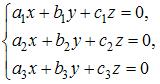имеет только одно нулевое решение, если определитель матрицы системы не равен нулю:

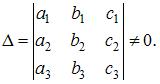
Тогда

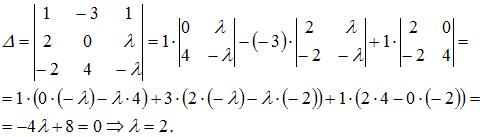
Значит, если 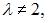то у данной системы будет единственное нулевое решение.

38. Тема: Системы линейных уравнений

Однородная система 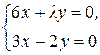имеет единственное решение, если 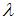принимает значения не равные …

Решение:
Система линейных однородных уравнений 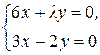имеет только одно нулевое решение, если определитель матрицы системы не равен нулю:
.

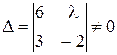Тогда

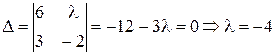
Зн Однородная система 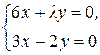имеет ачит, если 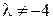, то у данной системы будет единственное нулевое решение.

39. Тема: Системы линейных уравнений

40.

Фундаментальное решение может быть вычислено для системы вида …

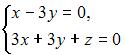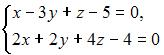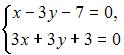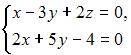Решение:
Фундаментальное решение может быть вычислено для однородной системы линейных алгебраических уравнений. Однородной системой линейных алгебраических уравнений называется система, все свободные члены которой равны нулю, например, система

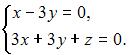
41. Тема: Системы линейных уравнений

Решение системы линейных уравнений 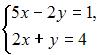методом Крамера может иметь вид …

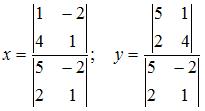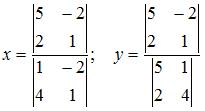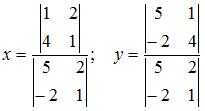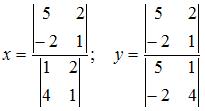Решение:
Решение системы n линейных уравнений с n неизвестными определитель которой 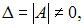находится по формулам Крамера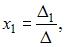
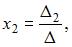
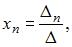
где 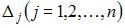– определитель, полученный из определителя системы заменой j-го столбца столбцом свободных членов. То есть

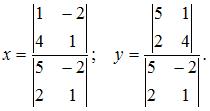
Тема: Системы линейных уравнений
Единственное решение имеет однородная система линейных уравнений …

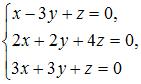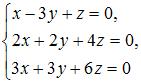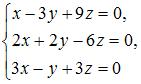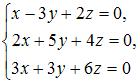Решение:
Однородная система линейных алгебраических уравнений имеет одно единственное решение, если ее определитель не равен нулю.
1. Из системы 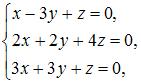получим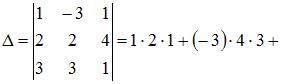

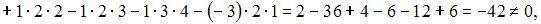
следовательно, система имеет единственное решение.
2. Из системы 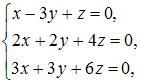получим так как последние две строки пропорциональны.
3. Из системы 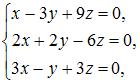получим 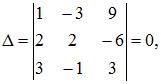так как последние два столбца пропорциональны.
4. Из системы 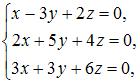получим так как первый и третий столбцы пропорциональны.

Тема: Прямая на плоскости

1. Уравнение прямой, проходящей через точку 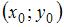с угловым коэффициентом 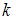, имеет вид: .

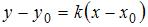2. Прямая, проходящая через две данные точк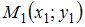и и 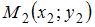, задается уравнением вида: .

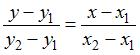Тема: Прямая на плоскости
Прямая линия проходит через точк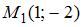и и 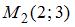. Тогда она пересекает ось 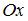в точке …

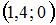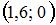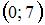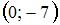Решение:
Прямая, проходящая через две данные точк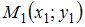и и 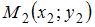, задается уравнением вида: 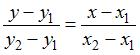. Тогда 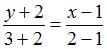, или 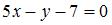. Точка, лежащая на оси 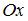, имеет координаты 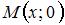. Тогда 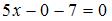и .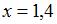

Тема: Прямая в пространстве

Возьмем произвольную прямую (рис. 1) и вектор 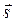={m; n; p}, параллельный ей. Вектор 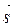называется направляющим вектором прямой. Пусть

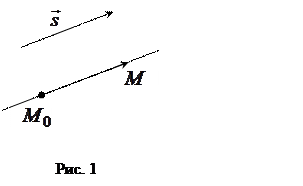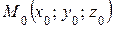- точка, лежащая на прямой. Другая точка 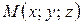принадлежит прямой тогда и только тогда, когда векторы 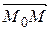и 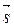коллинеарны, и, следовательно их координаты пропорциональны:

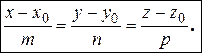(1)

Полученные уравнения (1) называют каноническими уравнениями прямой в пространстве.

Обозначив коэффициент пропорциональности в соотношении (1) через 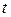, получим параметрические уравнения прямой в пространстве:

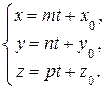
Тема: Обратная матрица

Для матрицы 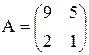обратная матрица 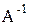имеет вид …

Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть
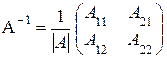– обратная матрица. Вычислим последовательно

,

,

,

,

.

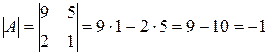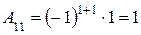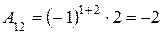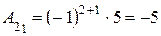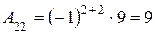Тогда .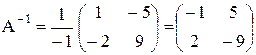

21. Тема: Обратная матрица
Для матрицы 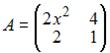не существует обратной, если значение x равно …

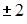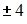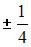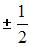Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

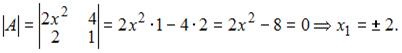
22. Тема: Обратная матрица
Для матрицы A существует обратная, если она равна …

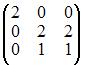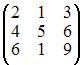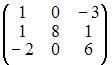Решение:
Всякая невырожденная квадратная матрица имеет обратную матрицу, то есть матрица имеет обратную, если определитель матрицы не равен нулю. Тогда вычислим определители 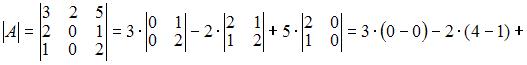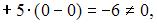то есть для матрицы 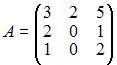существует обратная.
Так как определители остальных матриц равны нулю, то для них обратной матрицы не существует.

23. Тема: Обратная матрица
Для матрицы 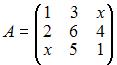не существует обратной, если значение x равно …

			– 2
			– 1

Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

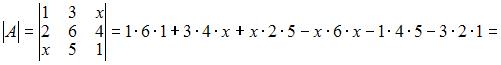
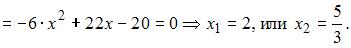
Тема: Обратная матрица
Для матрицы 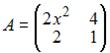не существует обратной, если значение x равно …

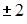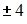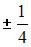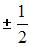Решение:
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть

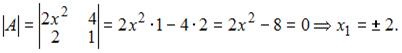
24. Тема: Обратная матрица
Для матрицы A существует обратная, если ее определитель …

Наши рекомендации Системы линейных уравнений. Определение 21:Системой m линейных уравнений с n неизвестными называется система вида: Системы линейных уравнений. Задание 18. Записать систему линейных уравнений Решение систем линейных алгебраических уравнений. Системы линейных алгебраических уравнений можно решать также, используя команду solve Системы линейных уравнений. Совместимость. Определенность. Равносильность. Формулы Крамера решения системы линейных уравнений Тема 2. Системы линейных уравнений Тема 2. Системы линейных уравнений Тема 2. Системы линейных уравнений Тема 2. Системы линейных уравнений Система линейных уравнений. Абсолютная погрешность и невязка решения системы линейных уравнений Тема 6. Системы линейных уравнений ← Предыдущая страница | Следующая страница →