Теоремы сложения и умножения. независимость событий. вероятность наступления хотя бы одного события из нескольких независимых

Пусть А и В два события. Тогда

Р (А +В) = Р(А) +Р(В) - Р(АВ) (3.1)
Для несовместных событий Р(А+В)=Р(А)+Р(В).
В случае трех событий А,В, С

Р(А +В+С) =Р(А) +Р(В) +Р(С) – Р(АВ) – Р(ВС) – Р(СА) + Р(АВС) (3.2)

Для попарно несовместных событий А,В,С Р(А+В+С)=Р(А)+ Р(В)+ Р(С).

Для двух событий А и В (Р(В)>0) вероятность наступления события А при условии, что произошло событие В, определяется равенством

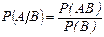(3.3)

Для 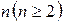событий 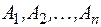справедливо соотношение, называемое формулой умножения событий:

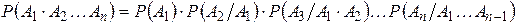(3.4)

Два события А и В называются независимыми, если выполняется равенство

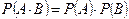(3.5)

События 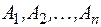называются попарно независимыми, если для любых двух событий А_i и А_j выполняется равенство

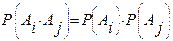(3.6)

т.е. А_i и А_j независимы (i¹j).

События 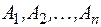взаимонезависимы, или независимы в совокупности, если для любых целых k и 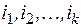таких, что 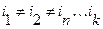, справедливо равенство

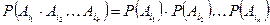(3.7)

ЗАДАЧИ

1. Монету подбросили три раза. Событие А - первый раз выпал герб. Событие В - число выпавших гербов больше числа выпавших цифр. Найти вероятность этих событий и проверить независимы ли они.

2. В группе 20 студентов, из них 15 человек получают стипендию. На дежурство по жребию отобрали двух студентов. Событие А - оба получают стипендию, В - первый из отобранных получает стипендию. Определить, зависимы ли события А и В и найти их вероятности.

3. В урне 10 белых и 5 черных шаров. Вытаскивают 3 шара случайно и без возвращения. Какова вероятность того, что они все одного цвета ? Какова вероятность того, что первый шар белый ? Зависимы ли события ?

4. События А и В несовместны, Р(А)¹0, Р(В)¹0. Зависимы ли данные
события ?

5. Студент знает 10 из 30 вопросов программы. Используя теорему умножения вероятностей, определить вероятность того; что из трех предложенных ему экзаменатором вопросов студент знает а) все три вопроса; б) хотя бы один вопрос.

6. На одиннадцати карточках написано слово «производная». По одной выбирают четыре карточки. Какова вероятность того, что в порядке выхода можно прочитать слово «овод» ?

7. В коробке 9 новых теннисных мячей. Для игры берут три новых мяча. После игры их возвращают обратно. При выборе мячей новые от бывших в игре не отличаются. Какова вероятность того, что после трех игр в коробке не останется новых мячей?

8. В новогодней лотерее 20 билетов, из которых 10 выигрышных. Студент купил два билета какова вероятность того, что оба выиграют? Хотя бы один выиграет?

9. Два пеленгатора с целью обнаружить радиостанцию осуществляют независимо одновременную разведку сигналов этой станции с различных направлений на установленной ранее частоте. Определить вероятность удачного исхода разведки одновременно с двух направлений, если вероятность определения пеленга с одного направления равна 0,6 и с другого 0,7 ?

10. Вероятность того, что в электроцепи напряжение превысит номинальное значение равна 0,9. При повышенном напряжении вероятность отказа прибора равна 0,8. Определить вероятность отказа вследствие повышения напряжения.

11. При браковке деталей обнаружено, что первый дефект присутствует в среднем в двух деталях из каждых 25. В случае его отсутствия, второй присутствует в трех деталях из каждых 50. Какова вероятность взять бракованную деталь?

12. Вероятность занятости первой линии связи 0,3 , второй - 0,6 , третьей - 0,2. Какова вероятность того, что все три линии свободны?

13. На заводе три цеха. Вероятность того, что первый цех выполнит месячный план - 0,9 , второй - 0,8 , третий - 0,95. Завод выполнит план, если план выполнят хотя бы два цеха. Какова вероятность того, что завод выполнит план?

14. Два стрелка стреляют по мишеням по одному разу. Вероятность того, что попадет первый стрелок - 0,9 , второй - 0,6. Второй стрелок получает приз, если его результат не хуже, чем у первого. Какова вероятность того, что он получит приз ?

15. В цехе имеются два станка, вероятность занятости каждого из них равна 0,7. Какова вероятность, что один занят, а другой нет?

16. В блоке, содержащем 24 лампы, отказала одна лампа. Неисправность отыскивается путем поочередной проверки. Найти вероятность того, что неисправность будет устранена не более, чем при первых трех попытках.

17. Электрическая цепь между точками А и В составлена по схеме, изображенной на рисунке. Различные элементы цепи выходят из строя независимо один от другого. Вероятности выхода элементов из строя за время Т следующие:

Элемент K₁ K₂ Л₁ Л₂

Вероятность 0,1 0,2 0,4 0,5

Определить вероятность прерывания питания за указанный промежуток времени.

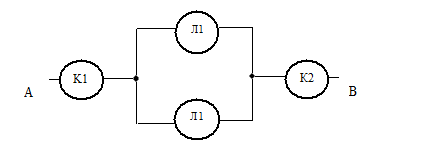
Рисунок 3

18. Доказать, что если Р(А) + Р(В) > 1, то А и В совместны.

19. Доказать, что если Р(А/В)>Р(А), то и Р(В/А) > Р(В).

20. Доказать, что если А и В независимы, то и 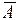, В, и 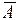, 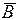независимы.

21. Доказать, что если Р(А+В)=1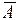–Р( ) ×Р( 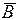), то события А и В независимы.

22. В коробке 6 ламп, из которых 4 бракованных. Некто наугад берет лампочку, ввинчивает в патрон и включает ток. Если лампа горит, то испытания прекращаются. Если лампа не горит, то она выбрасывается и испытывается следующая и т.д. Какова вероятность того, что будет проведено не более трех испытаний ?

23. В партии из 10 изделий содержится 5 бракованных. Для проверки контролер берет наугад одно изделие из партии и проверяет его качество. Если изделие оказывается бракованным, дальнейшие испытания прекращаются, а партия задерживается. Если изделие окажется стандартным, то контролер берет следующее изделие и т.д. Какова вероятность того, что будет проверено не более трех изделий.

24. Двое игроков бросают монету два раза каждый. Какова вероятность того, что у обоих игроков выпадет одинаковое число гербов ?

25. Производится стрельба по некоторой цели, вероятность попадания в которую при каждом выстреле равна 0,6 . Стрельба прекращается при первом попадании в цель. Найти вероятность того, что будет произведено не более четырех выстрелов.

26. Вероятность того, что разговор можно вести по каждому из трех каналов связи, соответственно равна 0,8 ; 0,7 ; 0,8 . Какова вероятность того, что разговор состоится ?

27. В комплекте имеется 12 телефонных аппаратов, среди которых 3 бракованных. Какова вероятность, что среди двух взятых аппаратов хотя бы один небракованный?

28. Вероятность соединения при телефонном вызове 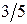. Какова вероятность, что соединение произойдет только при третьем вызове?

29. Вероятность появления поломок на каждой из трех соединительных линий равна 0,2 . Какова вероятность, что хотя бы одна линия исправна ?

30. На предприятии три телефона. Вероятности занятости их соответственно равны 0,6 ; 0,4 ; 0,5 . Какова вероятность, что хотя бы один из них свободен ?

31. Два пеленгатора независимо друг от друга пеленгуют объект. Первый имеет вероятность успеха 0,3 , второй - 0,4 . Какова вероятность, что объект будет запеленгован ?

32. По радиолинии передается сигнал в виде последовательности пяти импульсов. Вероятность искажения каждого импульса равна 0,1. Искажения отдельных импульсов независимы. Найти вероятность того, что передаваемый сигнал будет искажен.

33. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый делает по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что приз будет получен.

34. Вероятность хотя бы одного попадания в цель при трех выстрелах равна 0,936. Найти вероятность попадания в цель при одном выстреле.

4 ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА

Пусть даны события 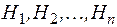образующие полную группу попарно несовместимых событий, и некоторое событие А. Его вероятность может быть найдена по формуле полной вероятности

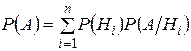(4.1)

При выполнении этих же условий для любого 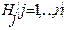справедлива формула Байеса

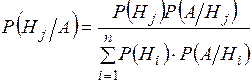(4.2)

События 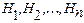часто называют гипотезами. Формула Байеса позволяет найти апостериорную, (послеопытную) вероятность гипотезы, если наступление события А считать результатом опыта. Вероятности 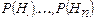называются априорными (доопытными).

ЗАДАЧИ

1. Кинескопы для цветных телевизоров производят три завода. Годовой выпуск кинескопов на П и III заводах одинаков, а первый завод производит на 50% меньше продукции, чем второй. В течение гарантийного срока не выходит из строя в среднем 50%, 60% и 70% кинескопов соответственно I, П, III заводов. Найти вероятность того, что кинескоп наугад приобретенного телевизора выйдет из строя до конца гарантийного срока.

2. Имеется три партии деталей, причем в первой - 2% брака, во второй -3% брака, в третьей - 4% брака. Какова вероятность взять бракованную деталь, если из выбранной наугад партии берется одна деталь ?

3. На трех автоматических линиях изготавливаются одинаковые детали. Первая линии дает 20%, вторая 40% всей продукции. Вероятность получения бракованной продукции на каждой линии соответственно равны 2%, 3% и 5%. Определить вероятность того, что взятая наудачу деталь окажется небракованной.

4. Известно, что 90% выпускаемой заводом продукции отвечает стандарту. Упрощенная схема контроля признает пригодной 95% стандартной и 2% нестандартной продукции. Определить вероятность того, что наудачу взятое изделие будет признано пригодным.

5. Имеются две партии одинаковых изделий по 10 и 15 штук. В первой партии 5 бракованных изделий, а во второй – 6. Наудачу взятое изделие из первой партии переложено во вторую, после чего из второй партии выбираются два изделия. Определить вероятность извлечения бракованных изделий из второй партии.

6. В трех аудиториях три группы абитуриентов. В 1-й – 39 человек, во 2-й –56, в 3-й – 46, причем в первой 4 медалиста, во второй – 3, в последней – 9. Экзаменатору по жребию досталась одна из аудиторий. Какова вероятность того, что случайно выбранный им абитуриент окажется медалистом ?

7. В ящике 10 новых теннисных мячей и 5 старых. Для первой игры берут случайно выбранный мяч, после игры возвращают. Для второй игры берут два мяча. Какова вероятность того, что они новые (не бывшие в употреблении)?

8. В университете среди выпускников 6 студентов получают именные стипендии, 120 студентов –«обычные» стипендии и 320 студентов стипендии не получают. Известно, что среди имеющих именные стипендии диплом с отличием получают 90%, среди имеющих «обычные» стипендии – 60%, среди остальных – 45%. Какова вероятность того, что наудачу выбранный студент получит диплом с отличием?

9. На одной из позиций импульсного кода с равными вероятностями передаются «единица» (импульс) и «ноль» (отсутствие импульса). Определить полную вероятность искажения помехами этой позиции, если вероятность преобразования «единицы» в «ноль» помехой равна 0,04 , а вероятность преобразования «ноля» в «единицу» равна 0,2.

10. Имеется два ящика с изделиями: в первом ящике 4 бракованных и 2 стандартных, во втором ящике 6 бракованных и 4 стандартных. Из первого ящика во второй наугад перекладывают два изделия, а затем из второго извлекают два изделия. Найти вероятность того, что оба извлеченных изделия будут стандартными.

11. В первом ящике содержится 5 изделий, из них 3 стандартных; во втором ящике 20 изделий, из них 15 стандартных. Из каждого ящика наугад извлекают по одному изделию, а затем из этих двух изделий взяли одно. Найти вероятность того, что взяли стандартное изделие.

12. В ящике находится 10 теннисных мячей, из которых 5 новых. Для каждой игры наугад берут два мяча. Найти вероятность того, что все мячи, взятые для второй игры, новые.

13. В урну, содержащую 3 шара, опущен белый шар. Какова вероятность извлечения одновременно из этой урны двух белых шаров, если все предположения о первоначальном числе белых шаров в урне равновероятны?

14. Вероятности подключения абонента к каждой из трех АТС соответственно равны 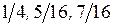. Вероятность соединения с абонентом подключения к первой АТС – 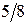, ко второй – 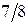, к третьей – ;

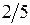а) Какова вероятность соединения?

б) Соединение произошло. Какова вероятность, что соединение произошло через вторую АТС?

15. Радиолампа, поставленная в телевизор, может принадлежать к одной из трех партий с вероятностями Р₁= Р₃= 0,25, Р₂= 0,5. Вероятности того, что лампа проработает заданное число часов, для этих партий равны соответственно 0,1 ; 0,2 ; 0,4.

а) Определить вероятность того, что лампа проработает заданное число часов;

б) Какова вероятность, что лампа принадлежит первой партии, если известно, что она проработала заданное количество часов?

16. Первая АТС работает 10 часов в сутки, вторая - 14. Вероятность соединения в случае работы первой АТС – 0,8 , в случае работы второй – 0,6 . Какова вероятность соединения ?

17. В урне 10 белых и 20 черных шаров. Подбрасывают игральную кость и добавляют в урну столько белых шаров, сколько выпало очков. Затем шары перемешивают и извлекают один. Он оказался белый. Какова вероятность того, что на игральной кости выпало 3 очка?

18. Два стрелка независимо друг от друга стреляют в цель, делая каждый по одному выстрелу. Вероятность попадания первого стрелка в цель 0,8 , второго - 0,4 . После стрельбы в мишени была обнаружена одна пробоина. Какова вероятность того, что она принадлежит первому стрелку ?

19. По цифровому каналу передаются символы «О» и «I», причем доля передаваемых нулей вдвое больше, чем единиц. Вероятность искажения символа «О» равна 0,06 , вероятность искажения «I» – 0,09. Найти вероятность искажения символа при передаче по этому каналу.

20. Прибор состоит из двух блоков, причем для функционирования прибора необходима исправная работа обоих блоков. Вероятность исправной работы первого блока в течение суток 0,8, второго - 0.7 . После испытаний прибора в течение суток было обнаружено, что прибор вышел из строя. Найти вероятность того, что первый узел исправен.

21. Изготовленные приборы сначала проверяет контролер в цехе, затем ОТК. Вероятность обнаружения неисправности контролером 0,8 , в ОТК-0,95. Известно, что прибор бракованный. Какова вероятность того, что неисправность обнаружит ОТК? Неисправность обнаружена. Какова вероятность, что ее обнаружил контролер?

22. Линия связи предназначена для передачи символов «О» и «I». При передаче символ с вероятностью 0,2 искажается (заменяется на противоположный). Для повышения надежности связи каждый из поступающих символов передается три раза («О» соответствует 000, «I» -III). Вместо переданной последовательности была принята 010. Какова вероятность, что был передан сигнал «О»?

23. В группе из 9 стрелков 5 отличных, 2 хороших, 2 удовлетворительных. Вероятность попадания в цель отличным стрелком равна 0,9 , хорошим – 0,7, удовлетворительным – 0,6. Наугад вызывается стрелок. Определить вероятность того, что вызванный стрелок попадет в цель.

24. В цехе работает 20 станков: 10 марки «I», 6 марки «П» и 4 марки «Ш» Вероятность произвести деталь отличного качества на станках марки «I» равна 0,9, «II» –0,8 и «III» – 0,7. Какой процент отличных деталей выпускает цех? Произвольно взятая деталь оказалась отличного качества. Какова вероятность, что она выполнена на станке марки «Ш»?

25. Радиолампы производятся на двух заводах. Первый поставляет 70%, второй -30% всей продукции. Из 100 ламп первого завода в среднем 80 стандартных, а из 100 ламп второго завода в среднем 60 стандартных. Какова вероятность, что произвольно взятая лампа будет стандартной? Произвольно взятая лампа оказалась стандартной. Какова вероятность, что она сделана на втором заводе?

26. Брак продукции завода вследствие первого дефекта составляет 8%. Причем среди бракованной продукции второй дефект составляет 4%, а в свободной от первого дефекта продукции второй дефект встречается в 2% случаев. Каков процент второго дефекта во всей продукции?

27. Имеется два комплекта одинаковых изделий по 12 и 10 штук. В каждом комплекте одно изделие бракованное. Наудачу взятое изделие из первого комплекта переложено во второй. После этого из второго комплекта наудачу вынимают изделие. Определить вероятность того, что оно бракованное.

5 СХЕМА БЕРНУЛЛИ

Пусть проводятся 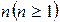независимых испытаний, в каждом из которых может быть два исхода, условно называемых «успех» и «неудача». Вероятность наступления «успеха» в каждом испытании одинакова и обозначается р, вероятность наступления «неудачи» q =1 – р. Вероятность наступления k (0 < k <n) успехов при n испытаниях обозначается через 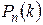. Справедлива формула Бернулли

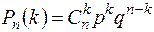, (5.1)

где 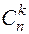число сочетаний из n no k:

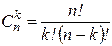
При изменении k от 0 до n величина 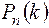принимает максимальное значение при некотором k = m. Величина m может быть найдена из неравенства

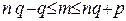
(Если выполняются оба неравенства для двух целых m₁ и m₂, то ).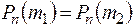

Обозначим через 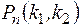вероятность того, что число «успехов» k при n испытаниях не меньше k₁ и не больше k₂ , т.е. 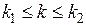Тогда из (5.1) следует

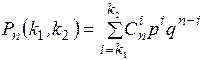(5.2)

Для вероятности хотя бы одного «успеха» можно использовать более простую формулу

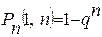(5.3)

В приложениях часто возникает задача определения числа испытаний n, необходимого для того, чтобы вероятность наступления хотя бы одного успеха была не меньше некоторой заданной величины g (0<g<1). Величина n удовлетворяет неравенству:

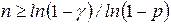(5.4)

ЗАДАЧИ

1. Станок-автомат выпускает 30% деталей высшего сорта. Найти вероятность того, что из шести случайно отобранных деталей будет: а) 4 высшего сорта; б) хотя бы 4 высшего сорта.

2. В институте 40% студентов имеют спортивный разряд. Какова вероятность того, что среди 5 случайно отобранных студентов разрядников будет: а) не меньше 3; б) меньше 3.

3. Вероятность того, что телевизор проработает гарантийный срок без поломки, равна 0,8. Закупили 4 телевизора. Какова вероятность того, что:

а) три телевизора не проработают гарантийный сроки; б) не менее двух проработают гарантийный срок.

4. Вероятность попадания в цель 0,7. Сделано 8 выстрелов. Какова вероятность того, что оказалось: а) пять попаданий; б) пять или шесть попаданий.

5. Вероятность того, что на один лотерейный билет выпадет выигрыш, равна 0,2. Куплено 5 билетов. Найти вероятность того, что: а) выиграют два билета; б) выиграют хотя бы три билета; в) не выиграют три билета.

6. По линии связи передают знаки 0 и 1. При передаче происходят ошибки, в результате которых с вероятностью 0,1 знак меняется на противоположный. Какова вероятность того, что при передаче сообщения из 5 знаков произойдет не более одной ошибки?

7. По каналу связи передается сообщение с помощью кода, состоящего из двух знаков. Вероятность появления первого знака 0,8. Всего передано 5 знаков. Найти вероятность того, что первый знак появится: а) два раза; б) два или три раза; в) не менее двух раз.

8. Вероятность правильного приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при шестикратной передаче сигнал будет принят: а) четыре раза; б) не менее четырех раз.

9. На заводе радиолампы выпускают два равномощных цеха, причем первый цех выпускает 10% ламп высшего сорта, второй -20%. Далее радиолампы раскладываются в коробки по четыре штуки. Найти вероятность того, что в коробке будет одна лампа высшего сорта, если известно, что:

а) лампы по коробкам раскладывают прямо в цехах; б) лампы поступают на склад, перемешиваются и только потом раскладываются по коробкам.

10. Что более вероятно выиграть у равносильного противника:

а) три партии из четырех или хотя бы три из пяти;

б) три партии из четырех или пять из восьми; в) не менее трех из четырех или не менее пять из восьми?

11. При выпуске интегральных схем на некотором предприятии доля

брака достигает 50%. Найти:

а) вероятность того, что из трех схем хотя бы одна бракованная;

б) сколько схем должно быть в случайно отобранной партии для того, чтобы с вероятностью 0,99 в ней оказалась хотя бы одна небракованная схема.

12. Известно, что вероятность выиграть хотя бы по одному лотерейному билету из трех равна 0,271. Какова вероятность выиграть по всем трем билетам.

13. Лампа сгорает раньше установленного срока в среднем в двух случаях из шести. В помещении установлены 6 ламп. Каково наиболее вероятное число ламп, которые выйдут из строя раньше срока? Какова вероятность этого?

14. На АТС поступают микросхемы, выпускаемые двумя предприятиями: 1-е поставляет вдвое больше схем, чем 2-е. На 1-ом 10% брака, на 2-м – 20% брака. В партии из трех изделий два бракованных. Какова вероятность того, что партия выпущена 1-м предприятием?