Привести запись системы линейных неравенств в матричном виде.
БИЛЕТ2
1)Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
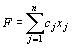 (1)
(1)
при условиях
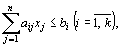 (2)
(2)
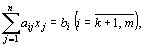 (3)
(3)
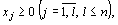 (4)
(4)
Функция (1) называется целевой функцией (или линейной формой) задачи (1) – (4), а условия (2) – (4) – ограничениями данной задачи.
Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1) при выполнении условий (2) и (4), где k = m и l = n.
Совокупность чисел 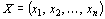 , удовлетворяющих ограничениям задачи (2) – (4), называется допустимым решением (или планом).
, удовлетворяющих ограничениям задачи (2) – (4), называется допустимым решением (или планом).
Значение целевой функции (8) при плане Х будем обозначать через 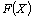 . Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство
. Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство 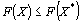 [соответственно
[соответственно 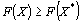 ].
].
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.
2) Множеством решений системы неравенств в целом является пересечение всех полуплоскостей, соответствующих отдельным неравенствам системы. Это пересечение и определяет множество допустимых планов. Это множество называется также областьюдопустимых планов (сокращенно ОДП). Оно представляет собой выпуклую многоугольную область.
В типичной, наиболее часто встречающейся ситуации, множество допустимых планов представляет собой ограниченную выпуклую многоугольную область — выпуклый многоугольник, расположенный в первой координатной четверти. Но возможны и другие варианты.
Если область допустимых планов непустая и ограниченная, то для каждой из задач — на максимум целевой функции или на минимум целевой функции, существует оптимальный план.
Если же область неограничена, то дело обстоит по-иному. В этом случае одна из задач (на максимум или на минимум целевой функции) или обе эти задачи могут оказаться неразрешимыми.
Полученные результаты можно сформулировать следующим образом.
Область допустимых планов задачи либо пуста, либо непуста. Если она пуста, то задача неразрешима, поскольку она не имеет даже допустимых планов.
Если область непуста, то она либо ограничена, либо неограниченна. Если область ограничена, то задача имеет решение.
Если же область неограниченна, то задача может иметь решение, а может не иметь его. Все зависит в этом случае от того, ограничена ли область в нужном направлении - в том направлении, в котором необходимо смещать линию уровня целевой функции до ее крайнего положения.
3)Решение:
Перепишем систему уравнений в матричном виде и решим его методом Гаусса
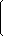 | -2 | 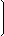 | |||
| -13 |
1-ую строку делим на 7
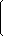 | -2/7 | 3/7 | 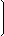 | ||
| -13 |
от 2; 3 строк отнимаем 1 строку, умноженную соответственно на 5; 9
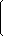 | -2/7 | 3/7 | 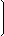 | ||
| 52/7 | -15/7 | ||||
| 95/7 | -118/7 |
2-ую строку делим на 52/7
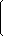 | -2/7 | 3/7 | 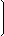 | ||
| -15/52 | 77/52 | ||||
| 95/7 | -118/7 |
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на -2/7; 95/7
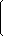 | 9/26 | 11/26 | 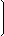 | ||
| -15/52 | 77/52 | ||||
| -673/52 | -993/52 |
3-ую строку делим на -673/52
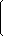 | 9/26 | 11/26 | 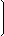 | ||
| -15/52 | 77/52 | ||||
| 993/673 |
от 1; 2 строк отнимаем 3 строку, умноженную соответственно на 9/26; -15/52
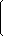 | -59/673 | 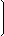 | |||
| 1283/673 | |||||
| 993/673 |
Ответ:
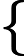 | x1 = -59/673 |
| x2 = 1283/673 | |
| x3 = 993/673 |
Билет № 3
1) Системы n линейных уравнений с n неизвестными x1, x2, ..., xn в общем случае принято записывать следующим образом:
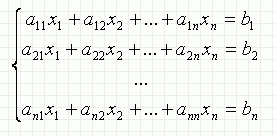
где аij и bi – произвольные константы. Число n неизвестных называется порядком системы.
Решением уравнения является такая совокупность значений переменных х1, х2,…, хn, которая одновременно обращает все уравнения системы в тождество.
Необходимым и достаточным условием существования и единственности решения системы уравнений является линейная независимость уравнений. Или, более точно, неравенство нулю определителя, составленного из коэффициентов системы уравнений:
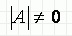
2) Параметрическое программирование (Макропрограммирование) - это язык программирования ЧПУ(Числовое программное управление).
В отличие от ЧПУ программирования, в параметрическом программировании расширяются возможности, сравнимые с объектно-ориентированными. Используя его системах управления ЧПУ становится возможным вариантность вычисления, применение логических операторов, работа с проходами инструмента, движениями манипуляторов. Возможность организации циклов, выбор по условию, переход, работа с подпрограммами. Добавляются элементы, осуществляющих полный контроль над ЧПУ - доступ к системным переменным и ячейкам программы электроавтоматики, возможность создавать свои собственные G-коды и функции, которые наиболее полно реализуют управление всех компонентов станка. Возможен доступ к параметрам ЧПУ, хранящим информацию об инструменте, положении рабочих органов, манипуляторов, системы координат, значений G-кода управляющей программы и ошибок. С помощью параметрического программирования можно разрабатывать диалоговые управляющие программы. Используя такие возможностями, имеешь один из эффективных способов управления станком, роботом, системой ЧПУ.
3) Целевая функция:
-4X1-2X2+1X3-1X4→max
Условия:
1X1-1X2+4X3-2X4=-1
3X1+2X2-1X3+4X4=-3
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:
1X1-1X2+4X3-2X4+R1=-1
3X1+2X2-1X3+4X4+R2=-3
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком
Так как среди исходного набора условий были равенства, мы ввели искуственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой расчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.
Из данных задачи составляем исходную симплекс таблицу.
| X1 | X2 | X3 | X4 | Своб член | |
| F | -1 | ||||
| R1 | -1 | -2 | -1 | ||
| R2 | -1 | -3 | |||
| M | -4 | -1 | -3 | -2 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -3, он задает ведущую строку - R2. В этой строке так же находим максимальный по модулю отрицательный элемент: -1 он находится в столбце X3 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X2 | X4 | Своб член | |
| F | -3 | |||
| R1 | -13 | |||
| X3 | -3 | -2 | -4 | |
| M | -13 | -7 | -14 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -13, он задает ведущую строку - R1. В этой строке так же находим максимальный по модулю отрицательный элемент. Так как в строке с отрицательным свободным членом нет отрицательных элементов, то система ограничений не совместна и задача не имеет решения.
БИЛЕТ 4 Целевая функция:
3X1+2X2→min
Условия:
1X1+2X2≤11
2X1-1X2≥5
1X1+3X2≥14
X1+0X2≥0
0X1+X2≥0
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:
1X1+2X2+X3=11
-2X1+1X2+X4=-5
-1X1-3X2+X5=-14
0X1+0X2+X6=0
0X1+0X2+X7=0
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Из данных задачи составляем исходную симплекс таблицу.
X1 X2 Своб член
F 3 2 0
X3 1 2 11
X4 -2 1 -5
X5 -1 -3 -14
X6 0 0 0
X7 0 0 0
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -14, он задает ведущую строку - X5. В этой строке так же находим максимальный по модулю отрицательный элемент: -3 он находится в столбце X2 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
X1 X5 Своб член
F 2.333 0.667 -9.333
X3 0.333 0.667 1.667
X4 -2.333 0.333 -9.667
X2 0.333 -0.333 4.667
X6 0 0 0
X7 0 0 0
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -9.667, он задает ведущую строку - X4. В этой строке так же находим максимальный по модулю отрицательный элемент: -2.333 он находится в столбце X1 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
X4 X5 Своб член
F 1 1 -19
X3 0.143 0.715 0.287
X1 -0.429 -0.143 4.144
X2 0.143 -0.285 3.287
X6 -0 0 0
X7 -0 0 0
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в строке F нет отрицательных элементов, то найдено оптимальное решение. Так как исходной задачей был поиск минимума, оптимальное решение есть свободный член строки F, взятый с противоположным знаком. Найдено оптимальное решение F=19 при значениях переменных равных: X1=4.144, X2=3.287,
Билет № 6
1) Привести свойства решений системы линейных неравенств.
Различают два типа линейных неравенств:
1) Строгие неравенства: 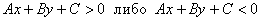 .
.
2) Нестрогие неравенства: 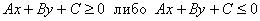
Решить линейное неравенство – это значит найти полуплоскость, точки которой удовлетворяют данному неравенству (плюс саму прямую, если неравенство нестрогое).Решение, как правило, графическое.
Система линейных неравенств – это, как вы понимаете, система, составленная из нескольких неравенств. Решить систему линейных неравенств – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы. Система линейных неравенств может не иметь решений, то есть, быть несовместной.Но самый распространённый случай, когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называетсямногоугольником решений системы.
2) Привести постановку транспортной задачи.
Транспортная задача. Один из экономико-математических методов. Цель: минимизация затрат при перевозке грузов. Транспортная задача может решаться в матричной или сетевой форме.
Решение транспортной задачи в матричной форме.
| потр пост | Р1 | Р2 | .. | Рm | ai |
| R1 | Х11 С11 | Х12 С12 | .. | Х1m | a1 |
| R2 | Х21 С21 | Х22 | .. | X2m | a2 |
| .. | .. | .. | .. | .. | .. |
| Rn | Хn1 | Хn2 | .. | Xnm | An |
| вj | в1 | в2 | .. | вm |
R1,R2,…,Rn- поставщики продукции, Р1, Р2, …, Рm- потребители продукции, n- количество поставщиков продукции, m- количество потребителей, х- размеры перевозки от «n» поставщика «m» потребителю. На первое место ставиться индекс строки (поставщика), на 2-е место- столбца (потребителя). В уголках пишутся критерии оптимальности, но я их писала не везде(С11, С12 …)- показатель который берется за основу д\минимизации затрат (расстояние, с\с, расходы). в1, в2,…-размеры потребления соответствующего потребител продукции. а1, а2,…- размеры поставок от соответствующих поставщиков.
а1= Х11 + Х12+…+Х1m и т.д. ;
b1 = Х11 + Х21 +…+ Хn1 и т.д. ;
Э=Х11*С11+Х12*С12+…+Хm*Сn+Xij*Cij- суммарные затраты по данному региону.
-целевая функция транспортной задачи (то к чему стремимся).
Алгоритм решения транспортной задачи.
1. Осуществляется постановка транспортной задачи, т.е строится матрица имеющая «m» поставщиков (строки) и «n» потребителей (столбцы). Затем в матрице указываются объемы ресурсов поставок и объемы потребления.
2. определяется тип задачи – закрытая или открытая. Условия закрытой тр-й задачи: Σai=Σbj, т.е сумма отправленных ресурсов должна ровняться размерам потребления. В случае если не равно – транспортная задача является открытой. Следует учесть, что решению подлежит только закрытая тр-я задача, следовательно открытую нужно привести к закрытой. Если Σai>Σbj вводится фиктивный потребитель (вводится дополнительный столбец) при этом объем потребностей Σai-Σbj=bф, Сij=0. Если Σai<Σbjвводится фиктивный поставщик Σai-Σbj=аф, Сij=0.
3. Составление опорного первоначального варианта прикрепления поставщиков к потребителям (метод северо-западного угла, метод двойного предпочтения, метод наименьшего значения критерия оптимальности).
4. Опорный план проверяется на вырожденность. Количество заполненных клеток матрицы должно равняться n+m-1.
5. Решение тр-й задачи по теореме Канторовича: план оптимален тогда и только тогда, когда каждой строке и столбцу матрицы могут быть присвоены любые произвольные числовые значения, называемые потенциалами, для которых соблюдаются следующие условия: 1) Vj – Ui ≤ Cij, Xij= 0 (для свободных клеток); 2) Vj – Ui = Cij, Xij >0 (для заполненных клеток), где Vj – потенциал столбца, Ui – потенциал строки.
Транспортная задача применяется в случае, когда имеется много поставщиков и много потребителей продукции. ТЗ является основой для рационального прикрепления поставщиков к потребителям, для рационального размещения перевозок в границах сети дорог.
3) Решить графическим и симплексным методом задачу линейного программирования. Сформулировать двойственную задачу и найти ее оптимальный план, используя теоремы двойственности.
Необходимо найти максимальное значение целевой функции F = 3x1+2x2 → max, при системе ограничений:
| x1+2x2≤12 | (1) |
| 2x1-x2≥7 | (2) |
| x1+3x2≥14 | (3) |
| x1+x2≥0 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом)
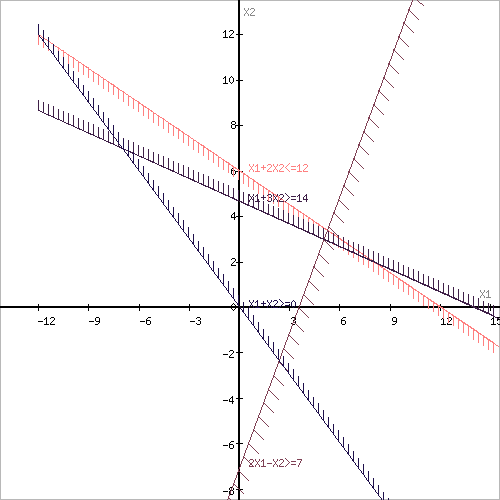
Границы области допустимых решений
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
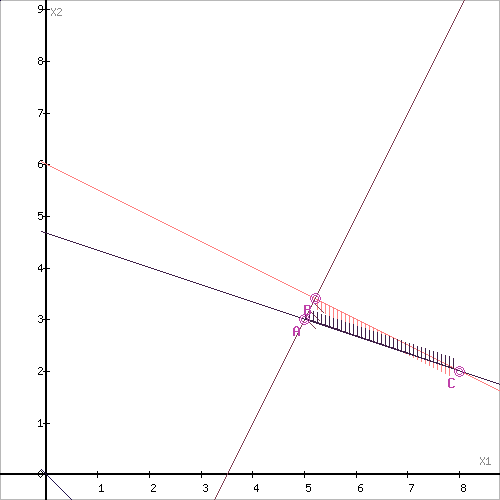
Рассмотрим целевую функцию задачи F = 3x1+2x2 → max.
Построим прямую, отвечающую значению функции F = 0: F = 3x1+2x2 = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
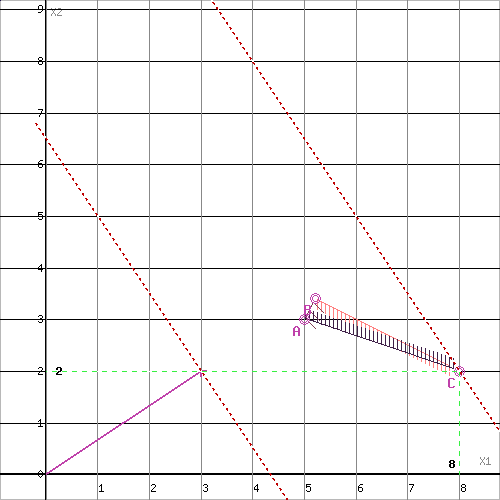
Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
x1+2x2≤12
x1+3x2≥14
Решив систему уравнений, получим: x1 = 8, x2 = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 3*8 + 2*2 = 28
симплексный метод
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:
1X1+2X2+X3=12
-2X1+1X2+X4=-7
-1X1-3X2+X5=-14
-1X1-1X2+X6=0
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком
Из данных задачи составляем исходную симплекс таблицу.
| X1 | X2 | Своб член | |
| F | -3 | -2 | |
| X3 | |||
| X4 | -2 | -7 | |
| X5 | -1 | -3 | -14 |
| X6 | -1 | -1 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -14, он задает ведущую строку - X5. В этой строке так же находим максимальный по модулю отрицательный элемент: -3 он находится в столбце X2 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X5 | Своб член | |
| F | -2.333 | -0.667 | 9.333 |
| X3 | 0.333 | 0.667 | 2.667 |
| X4 | -2.333 | 0.333 | -11.667 |
| X2 | 0.333 | -0.333 | 4.667 |
| X6 | -0.667 | -0.333 | 4.667 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -11.667, он задает ведущую строку - X4. В этой строке так же находим максимальный по модулю отрицательный элемент: -2.333 он находится в столбце X1 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X4 | X5 | Своб член | |
| F | -1 | -1 | |
| X3 | 0.143 | 0.715 | 1.002 |
| X1 | -0.429 | -0.143 | 5.001 |
| X2 | 0.143 | -0.285 | 3.002 |
| X6 | -0.286 | -0.428 | 8.003 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент - это -1 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X3, а ведущий элемент: 0.143.
| X3 | X5 | Своб член | |
| F | 6.993 | 28.007 | |
| X4 | 6.993 | 7.007 | |
| X1 | 2.002 | 8.007 | |
| X2 | -1 | -1 | |
| X6 | 1.002 | 10.007 |
Так как в строке F нет отрицательных элементов, то найдено оптимальное решение F=28.007
при значениях переменных равных: X1=8.007, X2=2,
Билет
1)Определить правило умножения вектора на число.
Умножение вектора на число. Определение. Произведением вектора 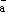 на действительное число
на действительное число  называется вектор
называется вектор 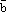 , удовлетворяющий следующим двум условиям:
, удовлетворяющий следующим двум условиям:
1) 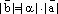 ; 2)
; 2) 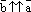 , если
, если 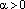 и
и 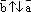 , если
, если 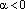 ; и обозначается
; и обозначается 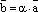 .
.
Теорема. (Свойства умножения вектора на число.)1. Свойство ассоциативности: 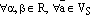 верно равенство
верно равенство 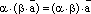 2. Свойство дистрибутивности умножения относительно сложения чисел:
2. Свойство дистрибутивности умножения относительно сложения чисел: 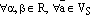 верно равенство
верно равенство 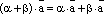 . 3. Свойство дистрибутивности умножения относительно сложения векторов:
. 3. Свойство дистрибутивности умножения относительно сложения векторов: 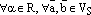 верно равенство
верно равенство 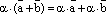 4.
4. 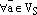 верно равенство
верно равенство 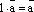 .
.
2) Дать понятие условного экстремума функции нескольких переменных. Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи.
Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи. Тогда u = f(x, y(x)). 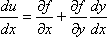
В точках экстремума: 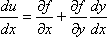 =0 (1)
=0 (1)
Кроме того:
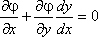 (2)
(2)
Умножим равенство (2) на число l и сложим с равенством (1).
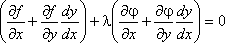
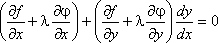
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
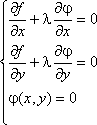
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум. Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.
Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи: 2x + 3y – 5 =
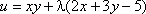
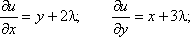
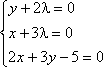
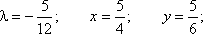 Таким образом, функция имеет экстремум в точке
Таким образом, функция имеет экстремум в точке 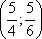 . Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа. Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
. Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа. Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
3)Решить систему уравнений методом Жордана- Гаусса
x1+2x2-x3=6
-x1+2x2+2x3=5
4x2+x3=10
Решение:
Перепишем систему уравнений в матричном виде и решим его методом Гаусса
1 2 -1 6
-1 2 2 5
0 4 1 10
от 2 строк отнимаем 1 строку, умноженную соответственно на -1
1 2 -1 6
0 4 1 11
0 4 1 10
2-ую строку делим на 4
1 2 -1 6
0 1 0.25 2.75
0 4 1 10
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на 2; 4
1 0 -1.5 0.5
0 1 0.25 2.75
0 0 0 -1
Ответ:
Система уравнений не имеет решений так как: 0 ≠ -1
Билет №10
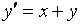 ,
,
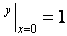
методом Эйлера–Коши на отрезке [0; 0,4]. Найти решение на равномерной сетке с шагом 0,1 в четырёх узловых точках.
Решение. Формулы (8.7) в данном случае примут вид
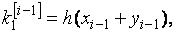
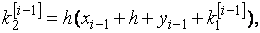
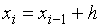
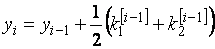
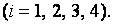
Полагая 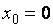 ,
, 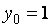 , последовательно находим
, последовательно находим
при 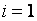
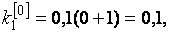
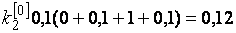 ;
;
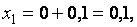
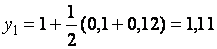 ;
;
при 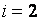
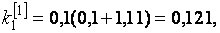
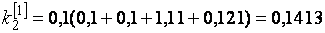 ;
;
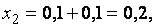
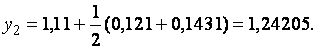
Далее получаем
при 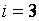
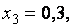
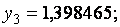
при 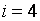
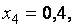
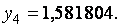
Погрешность полученного решения не превышает величины
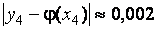 .
.
Билет
Вопрос
Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
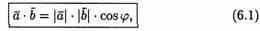
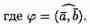
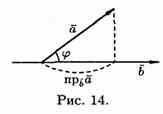
Формуле можно придать иной вид. Так как | a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab=ba
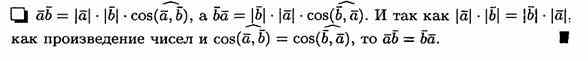


Вопрос
Определение 1.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
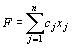 (8)
(8)
при условиях
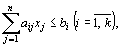 (9)
(9)
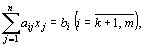 (10)
(10)
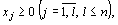 (11)
(11)
где 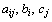 - заданные постоянные величины и
- заданные постоянные величины и 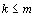 .
.
Определение 2.
Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.
Определение 3.
Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.
Определение 4.
Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.
Определение 5.
Совокупность чисел 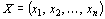 , удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).
, удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).
Определение 6.
План 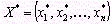 , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
Значение целевой функции (8) при плане Х будем обозначать через 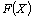 . Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство
. Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство 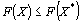 [соответственно
[соответственно 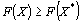 ].
].
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.
Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.
В том случае, когда требуется найти минимум функции 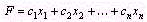 , можно перейти к нахождению максимума функции
, можно перейти к нахождению максимума функции 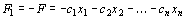 , поскольку
, поскольку 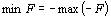 .
.
Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ 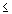 ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “
”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ 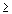 ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
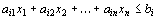
преобразуется в ограничение-равенство
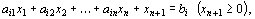 (12)
(12)
а ограничение-неравенство
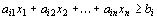
– в ограничение-равенство
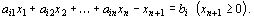 (13)
(13)
В то же время каждое уравнение системы ограничений
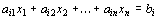
можно записать в виде неравенств:
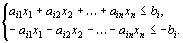 (14)
(14)
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
Отметим, наконец, что если переменная 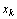 , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
, не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными 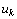 и
и 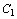 , приняв
, приняв 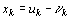 .
.
Вопрос
Умножение матрицы на число: Пусть 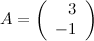 . Найти матрицу
. Найти матрицу 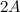
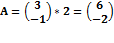
Билет № 14
1)Произведение матрицы А порядка p*n и матрицы В порядка n*q - это такая матрица С порядка p*q, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,
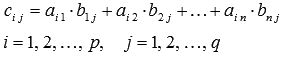
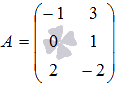 Пример
Пример
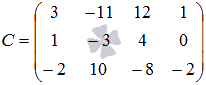
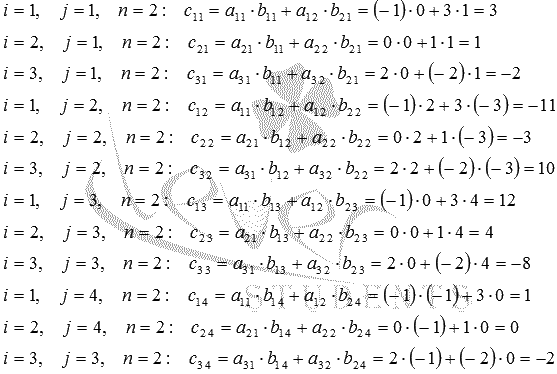
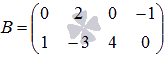
2)Определение. Условным экстремумом функции z = f (х, у) называется экстремум этой функции, достигнутый при условии, что переменные х и у связаны уравнением 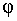 (х, у) = 0 (уравнением связи).
(х, у) = 0 (уравнением связи).
Определение 7.4 Пусть функция 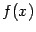 определена в некоторой окрестности
определена в некоторой окрестности 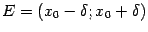 ,
, 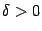 , некоторой точки
, некоторой точки 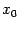 своей области определения. Точка
своей области определения. Точка 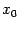 называется точкой локального максимума, если в некоторой такой окрестности
называется точкой локального максимума, если в некоторой такой окрестности 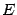 выполняется неравенство
выполняется неравенство 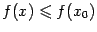 (
( 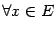 ), и точкой локального минимума, если
), и точкой локального минимума, если 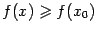
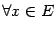 .
.
Если точка 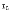 -- это точка локального экстремума функции
-- это точка локального экстремума функции 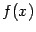 , и существует производная в этой точке
, и существует производная в этой точке
