Конспект лекций по курсу Основы теории эксперимента

Конспект лекций по курсу Основы теории эксперимента

Лекция 1 Основы теории эксперимента -основные понятия и определения

Любому виду испытания предшествует план эксперимента.

Планирование экспериментов — проведение специально спланированных исследо-ваний, опирающихся на статистическую обработку данных, для получения результатов с определенным уровнем доверия. Эти данные затем могут быть использованы для про-верки их соответствия определенному стандарту или сравнительной оценки нескольких систем. Специальная организационная подготовка и условия, в которых должны быть проведены эксперименты, носят название планирования экспериментов, а само плани-рование осуществляется с целью определения условий, при которых должны выполняться эксперименты.

Корректно поставленные задачи и полное обеспечение исследований позволяют, реализовав эксперимент, получить в той или иной форме ответы на поставленные исследователем вопросы. Причем стратегия и тактика исследований определяются общей методологией и частными методиками исследований.

Методология и методика

Методология научного познания, в общем широком смысле, базируется на диалектике – науке о наиболее общих свойствах, связях и законах бытия. Из общего диалектического подхода вытекает метод – правила познавательной деятельности или способ осуществления этой деятельности, определяющий ее структуру, т.е. некоторую совокупность операций, применяемых для решения задач определенного класса.

В качестве примера может быть приведен исторический метод – способ решения задач познания путем воспроизведения их истории (генезиса проблемы) или логический метод-способ решения задач познания путем воспроизведения таких сторон объекта, которые характеризуют его относительную стабильность, инвариантность (например, тип кристаллической решетки).

Примерами общенаучного методологического подхода являются также системно-структурные и статистические методы. О методологии современного инженерного эксперимента можно говорить, если имеется общая методика для исследования объектов или процессов разной физической природы.

Следующий этап реализации эксперимента – это методика исследований, т.е. совокупность способов и приемов проведения экспериментальных исследований, обеспечивающих получение единообразного (статистически однородного) и достоверного (воспроизводимого) эмпирического материала.

Поскольку методология современного инженерного эксперимента как обязательный этап включает формализацию объекта и моделирование, остановимся на последнем. Модель – это абстрактный или конкретный объект, отражающий структуру и поведение реального объекта или процесса. Например, простейшая модель решения инженерной задачи может быть представлена в виде блок-схемы (рис. 1).

В настоящее время моделирование приобретает роль общего метода научного исследования.

Рисунок 1 Блок-схема решения исследовательских задач

Понятие модели непрерывно развивается. До XIX века подобием оперировали только в механических представлениях. Сейчас в основе моделирования лежит теория подобия. Основной ее постулат: объекты подобны, если между ними наблюдается соответствие, определяемое критериями подобия – безразмерными комплексами параметров процесса и системы, в которой он протекает. Примерами подобных комплексов будет число Рейнольдса в гидравлике, Прандтля – в теплотехнике, Маха – в аэродинамике.

Модели могут быть материальными (вещественно-агрегатными), мысленными (программы ЭВМ) и знаковыми (химические символы элементов).

Следует иметь в виду, что модели, отвечающие физике параметров или процессов (физические законы), можно получить в технических экспериментах только на основе теоретических предпосылок, а не непосредственно из результатов экспериментов. Это объясняется тем, что любые экспериментальные результаты (обычно ряды чисел) можно аппроксимировать целым набором различных математических функций. Но из-за ограниченности интервалов варьирования факторов структура этих функций (моделей) может никак не соответствовать реальному физическому содержанию исследуемых процессов. Примером могут служить известные эмпирические формулы резания металлов.

Эти обстоятельства подтверждают существенность связи экспериментальных исследований с теоретическими. «Ни одно исследование не может назваться истинной наукой, если оно не прошло через математические доказательства» (Леонардо-да-Винчи).

Переход от эмпирического к теоретическому уровню – это не просто перевод знаний с обыденного языка на научный, а изменения в содержании и форме знаний. По П. Ланжевену: «Теория превращает новые факты в новые принципы».

Выдвигая новое теоретическое построение, мы опровергаем что-то старое и одновременно доказываем что-то новое. Теоретическое мышление отражает объект со стороны его внутренних связей и закономерностей, постигаемых путем рациональной обработки экспериментальных данных. Теоретические исследования общи, а экспериментальные – отражают лишь часть сущности.

Научная теория – это объединенная единым началом система суждений, включающая относительно законченные мысли, отражающие объекты, явления, их свойства, связи и отношения.

Однако утверждение, что эксперимент лишь доказательство истинности теории или орудие построения новых гипотез, неверно. Результаты всякого научного эксперимента не только отражают имеющиеся теоретические построения, но и являются самостоятельным носителем объективной информации.

Результаты исследований

Характерной особенностью подавляющего числа инженерных исследовательских задач является сочетание подчеркнуто конкретного задания с неопределенностью в выборе решений, т.е. с большой творческой свободой. Следовательно, инженер-исследователь вынужден определить возможность построения системы альтернатив при решении задачи, т.е. выдвинуть ряд гипотез.

Системный подход

В современной науке происходит быстрый рост интегральных задач синтеза, требующих междисциплинарных исследований. Разработка их привела к объединению научных методов и установлению общих закономерностей для различных объектов и традиционных научных дисциплин.

Русский врач, философ и общественный деятель А.А. Богданов разработал в начале XX века общую теорию систем, названную им тектологией.

Система – это ряд элементов, взаимосвязанных структурно и функционально. Понятие системы относительно: любая система включает подсистемы и сама является подсистемой более общей системы.

Теория систем – это формальная эмпирико-интуитивная дисциплина, применимая ко всем наукам, имеющим дело с системами.

Условия существования систем могут быть сформулированы следующим образом:

есть набор объектов;

есть набор признаков каждого объекта;

есть набор признаков набора объектов;

есть набор признаков набора признаков объектов.

Каждое из этих условий необходимо, но только их сумма позволяет выделить систему.

Первые два условия – это условия актуальности, т.е. наблюдаемые объекты становятся претендентами на включение их в систему. Третье - определяет связь между объектами, четвертое – связь между признаками объектов.

Каждая система может быть выделена гипотетической оболочкой (воображаемой контрольной поверхностью, логической границей) из ее окружения.

К внутренним связям системы можно отнести следующие:

- структурные (связи субординации);

- генетические (связи развития);

- координационные (связи взаимодействия);

- функциональные (связи назначения).

Связь системы с окружением определяется входом и выходом. Отсюда функция системы – это преобразование входов в выходы. Оно может моделироваться терминологически, математически, физическими аналогами, знаковыми системами и т.п.

Система разомкнутая (открытая), если существует обмен массой, энергией, информацией с окружающей средой. Система замкнута (закрыта), если этот объем пренебрежимо мал.

Структурное описание системы – это ее внутренние параметры, функциональное – внешние.

При существующем уровне знаний понимание сложных систем возможно только при выделении отдельных срезов системы – ее функциональных плоскостей с собственным специфическим входом-выходом.

Например, в измерительной системе можно выделить срезы преобразования, коммутации, фиксации и т.п.

Итак, общая схема системного подхода включает этапы, характеризующие структуру выделенной системы.

В существующем виде системный подход эффективно выполняет постановку проблемы, базируясь на дескриптивном (описательном) анализе и систематизации существующего знания, т.е. априорной информации. Накопление огромной ее массы не только не облегчает, но значительно усложняет представление об исследуемом объекте.

Любая общая картина сложного объекта всегда остается неполной и односторонней. Выступая с анализом, системный подход выделяет свойства, делающие объект частью целого, а – с синтезом – позволяет представить целое, состоящее из отдельных частей. Здесь большую роль играет принцип формализации – уточнения содержания посредством выявления его формы.

Классификация

Классификация любых объектов неразрывно связана с системным подходом и является его логической конкретизацией и развитием. Первая операция, производимая исследователем над множеством данных априорной информации, включает изучение его организации, т.е. разнообразия входящих в него объектов и их связей.

Систематизация объектов информационного множества может быть выполнена путем разделения всего множества на группы в соответствии с обобщающими и дифференцирующими признаками. В качестве последних используют любой критерий, например, степень сложности объектов. Итогом систематизации должна быть классификация, которая не только делит все множество на отдельные группы и элементы, но и вскрывает связи между ними.

Следовательно, классификация требует знания соотношения целого и его элементов, а также структурных связей.

Основные типы связей включают следующее:

1. Относительные связи, когда самостоятельные объекты объединяются взаимодействием. Например: солнце и планеты.

2. Причинно-следственные связи. Например: отец и сын; нагрузка и напряжение.

3. Связь отношений двух и более сторон в едином целом. Например: полюса магнита.

4. Связь предшествующего состояния с последующим. Например: обкатка двигателя и его нормальная эксплуатация.

5. Сравнительная связь большого и малого. Например: толстолистовой и тонколистовой прокат.

В каждом явлении имеются внутренние элементы, его образующие, и соответствующая структура – способ их связи между собой. Каждый элемент, в свою очередь, обладает внутренней структурой.

При классификации особое внимание следует уделять единому обобщающему логическому признаку. Пренебрежение этим приводит к высказываниям типа: «Шел дождь и три студента. Один – в унынии, другой – в калошах, третий – в пивную».

Очень важным является требование выдерживать единый иерархический уровень признаков. Если в качестве такого признака выбрана степень важности элементов, то неверно утверждать, что человек состоит из головы, туловища, волос, ногтей и т.п.

Наконец, различительные признаки должны быть дискретными, т.е. позволять однозначно различать группы элементов классификации ( колба , цилиндр, пипетка), или, хотя бы, условно дискретными (колбы объемом 1 л , колбы объемом 500 мл., колбы объемом 250 мл)

К недостаткам различных классификационных подходов следует отнести следующее:

- значительный вклад субъективных качеств исследователя;

- неоднозначность, так как возможны различные варианты классификации;

- отсутствие возможности математизировать процесс и объективно оценить его качество.

Основой любой классификации являются признаки – характеристики, обобщаемые для всего множества объектов (например, измерительные инструменты). Признак n значим, если множество объектов разбито на n классов. Знать признак – это определить принадлежность к соответствующему классу, по крайней мере, одного объекта (например: микрометрические и штанген–инструменты).

Первоначальным этапом классификации является формализация описания множества объектов путем установления базисов – подмножеств фактически необходимых признаков. Базисная таблица идентификации включает столбцы – объекты и строки – необходимые и достаточные признаки для отделения каждого объекта от всех остальных.

Практически легче выделить признаки не путем их подробного описания, а путем сопоставления друг с другом.

Критерием разграничения различительных и избыточных признаков является их устранимость. Признак устраним, если объекты могут быть различимы без этого признака, т.е. эти признаки связывают систему с окружением – объектами в ней отсутствующими. При описании среды через систему они становятся наиболее существенными. Так, способность измерить размер является избыточным (не отличительным) признаком штанген и микрометрических инструментов, но этот признак позволяет объединить их и выделить из более общей группы инструментов, включающих еще калибры и эталоны.

Метод экспертных оценок

Само название метода свидетельствует о том, что к оценке априорной информации привлечен ряд экспертов. Это могут быть реальные люди (специалисты в данной области) или различные литературные источники (отчеты, статьи, монографии и т.п.), в которых опубликованы результаты подобных или аналогичных исследований.

Один из методов экспертных оценок, используемых для упорядочения исходной информации, называется априорным ранжированием. Он используется при низкой достоверности априорной информации, наглядно описанной логистической кривой (рис.2). При этом экспертная оценка является вероятностной, основанной на способности личности давать полезную информацию в условиях неопределенности. Неизвестная количественная характеристика исследуемого явления рассматривается как случайная величина, отражением точечной оценки которой является индивидуальное мнение специалиста, о значимости того или иного события, процесса, параметра.

Суть ранжирования или распределения по рангам заключается в присвоение отдельным факторам, которые, согласно априорной информации, могут влиять на объект исследования, определенного ранга – порядкового места. Вклад каждого фактора оценивается по величине ранга (порядковому номеру места), который отведен специалистом данному фактору при ранжировании (распределении по местам) всех факторов информационного множества.

Рисунок 2. Зависимость достоверности информации от ее типа

Ранжирование выполняется с учетом предполагаемого (зачастую количественно неизвестного) влияния каждого фактора на итоговый параметр (выход, результат). Таким образом, экспертами используется определенная шкала порядка, на которой заданный показатель определяет расположение объектов во всей их совокупности в соответствии с принятым масштабом шкалы. То есть каждому объекту соответствует некоторая количественная характеристика или мера. «Когда описание открывает путь для измерения, дискуссии заменяются вычислениями» (американский психолог С. Стивенс), т. е. оценка становится объективной.

Итак, ранжирование – процедура установления относительной значимости (предпочтительности) исследуемых объектов на основе их упорядочения.

Ранг – показатель, характеризующий порядковое место объекта в группе других объектов, обладающих существенными для оценки свойствами.

Точность и надежность процедуры ранжирования в значительной степени зависят от количества ранжируемых объектов. В принципе, чем меньше таких объектов, тем выше их различимость с точки зрения экспертов, а следовательно, тем более надежно можно установить их ранг. Количество ранжируемых объектов, как правило, не должно превышать 20, а наиболее надежные результаты относятся к 10 объектам.

Численность группы экспертов также имеет важное значение. При малом их числе теряется смысл коллективной оценки, так как резко возрастает влияние каждого эксперта. При большом – индивидуальная оценка практически не влияет на групповую и, кроме того, снижает уровень достоверности вследствие привлечения малоквалифицированных специалистов. В общем случае численность экспертов должна превышать число оцениваемых факторов, но быть меньше общего, потенциально возможного числа специалистов.

Практический выход априорного ранжирования состоит в следующем:

построение априорных диаграмм рангов, что при использовании литературных источников является, по существу, кратким наглядным обзором по теме исследований;

отбор наиболее значимых для исследования факторов, что сокращает объем и повышает эффективность исследований.

Таким образом, априорное ранжирование, являясь субъективным мнением экспертов в данной области, дает, тем не менее, объективную информацию, так как мнение специалистов объективно отражает реальное положение вещей в рассматриваемой области знаний.

Алгоритмизированная методика априорного ранжирования может быть представлена в виде нижеследующих основных этапов. В методике имеется реальный численный пример.

1. Постановка задачи исследований.

2. Выбор параметров выхода или отклика.

3. Составление перечней факторов, влияющих на изучаемый процесс.

4. Операционное определение факторов. Это определение вводится для однозначного понимания специалистами каждого фактора.

5. Установление интервалов варьирования отдельных факторов. Это связано с тем, что влияние отдельных факторов может быть различным в разных областях факторного пространства.

6. Ранжирование факторов в порядке убывания их воздействия на параметр выхода.

Каждому фактору из общего перечня присваивается ранг (цифра натурального ряда), соответствующий месту, отведенному исследователем данному фактору в ранжируемом ряду (наиболее важный фактор – 1, менее важный – 2, еще менее важный – 3 и т.д.).

7. Формальная проверка ранжирования.

Сумма рангов в каждом столбце

, (1)

где n – число рассматриваемых факторов.

8. Определение суммы рангов по факторам.

, (2)

где – ранг каждого i-го фактора у j-го специалиста (или по j-му источнику литературы); m – количество опрошенных экспертов (или рассмотренных литературных источников).

9. Определение средней суммы рангов.

. (3)

10. Определение абсолютной величины разности между каждой суммой рангов по факторам и средней суммой рангов.

. (4)

11. Определение квадрата разностей.

. (5)

12. Определение суммы квадратов разностей.

. (6)

13. Определение показателей групп связанных рангов.

, (7)

где t – количество одинаковых связанных рангов в j-м ранжировании; k – индекс величины одинаковых связанных рангов в j-м ранжировании.

14. Определение суммарного показателя связанных рангов по ранжированию.

, (8)

где p – число групп одинаковых связанных рангов в j-м ранжировании.

15. Определение суммы суммарных показателей связанных рангов.

. (9)

16. Определение коэффициента конкордации.

. (10)

Коэффициент конкордации W меняется от 0 до 1, причем равенство единице означает, что все эксперты дали одинаковые оценки по данному признаку, а равенство нулю означает, что связь между оценками, полученными от разных экспертов, не существует.

17. Предварительная оценка коэффициента конкордации.

18. Определение значимости коэффициента конкордации.

При числе факторов меньше или равном семи можно пользоваться специальной таблицей (расчетное должно быть больше критического, табличного). При большем числе факторов достаточно, чтобы значение расчетного критерия было больше значения табличного критерия для соответствующей степени свободы ( ) и доверительной вероятности (p), обычно принимаемой 0,95 или 0,99.

, (11)

. (12)

Примечание: при отсутствии связанных рангов величина обращается в нуль.

19. Построение априорных диаграмм рангов.

Получение значимого коэффициента конкордации (т.е. подтверждение согласованности мнений специалистов) дает возможность построить среднюю априорную диаграмму рангов в координатах: ордината – сумма рангов; абсцисса – ранжируемые объекты (факторы). Чем меньше сумма рангов данного фактора, тем выше его место на диаграмме (рис.3).

Рисунок 3. Диаграмма рангов

20. Принятие решений по стратегии последующего эксперимента:

Диаграмма рангов может иметь следующий вид:

20.1. Распределение (различие в рангах) факторов и их убывание равномерное. В этом случае уровень априорной информации весьма низок, и поэтому все факторы должны включаться в эксперимент.

20.2. Распределение равномерное, а убывание неравномерное. В этом случае, если возможно, лучше включить в физический эксперимент все факторы, но возможен и априорный отсев их.

20.3. Распределение неравномерное, а убывание равномерное. Возможен априорный отсев факторов с низким рангом.

20.4. Распределение и убывание неравномерное (например, экспоненциальное). Это наиболее благоприятная ситуация, так как нужно отсеить ряд факторов, отнесенных к шумовому полю.

Лекция2. Планирование однофакторных и многофакторных экспери-ментов

Однофакторным считается экспериментальные исследования, когда планируемое возмущающее воздействие направлено только на один фактор

Классический эксперимент

Классическим называют наиболее старый метод планирования и реализации экспериментов. Он предусматривает фиксирование на определённых уровнях всех переменных факторов, кроме одного, который принимает некоторые дискретные значения (уровни) в исследуемой части области своего существования. В результате находим зависимость исследуемой величины (параметра выхода) только от одного фактора. Математическая модель этой зависимости может быть получена в результате ряда геометрических построений или, чаще всего и с гораздо меньшей погрешностью, методом наименьших квадратов.

Поскольку этот метод не определяет структуру получаемой однофакторной модели и требует наличия перенасыщенной системы уравнений (число уравнений превышает число неизвестных) для вычисления параметров, на количество уровней переменного фактора налагаются определённые ограничения.

Если выход изменяется по закону, близкому к линейному, то для нахождения параметров линейной модели достаточно трёх точек на линии отклика. То есть достаточно варьировать переменный фактор на трёх дискретных уровнях. Однако вид линии отклика экспериментатору зачастую неизвестен. В этом случае естественное стремление сократить объём экспериментов вступает в противоречие с последующей возможностью функциональной или графической интерпретации их результатов. Последние могут подчиняться более сложному закону, (например, квадратичному) с большим числом параметров. Это обстоятельство заставляет планировать однофакторный эксперимент как минимум на четырёх уровнях переменного фактора. А при имеющейся опасности срыва одного из опытов необходимо предусмотреть пятую резервную точку.

Следует отметить, что если нелинейную экспериментальную зависимость линеаризовать логарифмированием (отложив на графике в логарифмическом масштабе), то можно для аппроксимации экспериментальных результатов использовать степенную или показательную функции.

Например,

(2.1)

имеем lg y=lg a + x×lg b, что эквивалентно линейной зависимости Y=A+xB при оперировании не самим результатом эксперимента, а его логарифмом.

Вычисления по определению параметров модели методом наименьших квадратов удобно выполнять в виде таблицы (табл.5.1).

Таблица 2.1

Лекции 2-3

ПЛАНИРОВАНИЕ МНОГОФАКТОРНЫХ ЭКСПЕРИМЕНТОВ

Многофакторным считаем эксперимент, когда планируемое возмущающее воздействие направлено одновременно на несколько переменных факторов. Причем, регрессионная модель исследуемого объекта может включать не только все переменные, но и эффекты их взаимодействий.

Эксперимент, в котором реализуются все возможные сочетания уровней выбранных факторов, называется полным факторным экспериментом.

Возникновение и развитие статистических методов планирования многофакторных экспериментов связано с именем Р. Фишера, издавшего в 1935 году монографию, посвященную планированию эксперимента и давшую название всему направлению. Фишеру принадлежит и термин “дисперсия”. Ф. Йетс предложил для полнофакторного эксперимента простую расчетную схему.

В 1945 году Д. Финни ввел дробные реплики, что позволило резко сократить число экспериментов.

Построение современной теории планирования эксперимента завершилось в 1947 году после создания Н. Винером кибернетики и формулирования им понятия “черный ящик”.

В России значительные разработки в области теории и практики планирования многофакторного эксперимента выполнены под руководством В.В. Налимова в МГУ.

В настоящее время можно с уверенностью утверждать, что разработаны все основные положения новой дисциплины “Математическая теория эксперимента”.

Основные термины и понятия

Цель любого экспериментального исследования – это раскрытие некоторых закономерностей функционирования рассматриваемых систем, т.е. нахождение функциональной связи, аппроксимирующей реальную зависимость между выходом и независимыми факторами. Эксперимент, в котором используется закономерное варьирование различных двух или более независимых факторов, называется многофакторным. Количество факторов обозначается буквой “k”.

Выход– это результат, численная характеристика цели исследования. Эквивалентными терминами являются: выходной параметр, критерий оптимизации, отклик, значение целевой функции и т.д. Обозначается буквой “y”.

Геометрическая интерпретация выхода представляет собой поверхность отклика (при двух факторах) или гиперповерхность отклика (более двух факторов).

Алгебраическая интерпретация выхода представляет собой функцию отклика или математическую модель процесса (уравнение регрессии, регрессионную модель).

Факторомназывается измеряемая переменная величина, принимающая определенные значения и воздействующая на рассматриваемую систему, т.е. на объект исследований. Обозначается буквой “x”.

Подавляющее число изучаемых объектов относится к классу сложных систем. В общем случае любой объект исследований можно представить в виде некоторого множества точек в факторном пространстве, которое может быть условно разбито на два подмножества: “черное” и “светлое”.

Первое, называемое “черным ящиком”, представляет собой кибернетическое понятие системы с неполным знанием механизма ее функционирования. В этом случае структура математической модели процесса неизвестна и модель может быть представлена в виде некоторой аппроксимирующей функции. “Светлый ящик” – подмножество с известным механизмом процесса, традиционными экспериментальными задачами и известной структурой модели, например, в виде различных физических законов.

На процесс исследований всегда накладываются ограничения, определяемые возможностями измерительной аппаратуры, стремлением к снижению временных затрат на постановку опытов и материальных – на материалы и приборы. Эти ограничения приводят к тому, что исследователь всегда располагает относительно небольшим объемом экспериментальных данных, на основании которых он должен делать выводы о свойствах и поведении объекта изучения. На результаты опытов, кроме того, влияет большое число случайных неуправляемых факторов. Последнее обстоятельство требует включения в рассмотрение не только оценки результатов, но и оценки их точности. Следовательно, необходима статистическая обработка данных.

Традиционными методами можно получить такие же результаты, как и многофакторными экспериментами. Однако там нет такой четкости и логически упорядоченной стратегии, так как исследователь ведет поиск, руководствуясь только своей интуицией. Это приводит, как правило, к постановке многих лишних опытов при снижении точностных характеристик выхода.

Кроме того, при планировании и реализации многофакторных экспериментов оценка параметров и установление доверительных границ для них производится по стандартной методике, что обеспечивает сопоставимость результатов данных исследователей на разном оборудовании, в разных странах.

Таким образом, математическое планирование экспериментов – это процедура выбора числа и условий постановки опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью, методов обработки результатов и принятия решений.

Критерии оптимальности факторных планов

Рассматривая планирование экспериментов как аналог раздела прикладной математики, можно сформулировать ряд положений, играющих роль аксиом. Этими положениями являются критерии оптимальности эксперимента. Все их можно условно разделить на две группы: статические и динамические.

Первые образуют мозаику взаимно несовместимых положений, из которых можно выделить лишь иерархически более важные.

Вторые – определяют оптимальную стратегию в последовательности проведения опытов.

Другая классификация выделяет критерии, связанные с точностью оценки коэффициентов регрессии, и критерии, определяющие ошибку в оценке поверхности отклика. На сформулированных на математическом языке критериях оптимальности строится вся теория математического планирования многофакторного эксперимента.

Критерий оптимизации

При постановке оптимизационных задач очень важно правильно определить параметр, который требуется оптимизировать. Эта часть исследований не поддается формализации и целиком зависит от опыта и интуиции исследователя.

Параметр оптимизации является реакцией (откликом) исследуемой системы на воздействие факторов. Поскольку реакция любого объекта исследований весьма многогранна, необходимо выбрать аспект реакции, представляющий наибольший интерес, то есть параметр оптимизации является количественной характеристикой цели исследований.

В качестве оптимизируемых характеристик в различных системах могут быть выбраны следующие параметры:

1. Технологические, связанные с процессом производства (жирность молока, твердость металла),

2. Конструктивные, определяющие конструкцию (зазор в подшипнике скольжения, толщина стен строения),

3. Материаловедческие, характеризующие свойства используемых материалов (прочность кирпича, негорючесть облицовки).

4. Эксплуатационные, служащие оценкой работы системы (ресурс двигателя, износостойкость подошвы).

5. Экономические (себестоимость, рентабельность).

Предпочтительно использовать количественные параметры, но могут быть выбраны и качественные:

– тип технологического процесса изготовления какой-либо детали;

– различные конструкции некоторого узла;

– марка или структура применяемого материала;

– ремонтопригодность или резервируемость;

– необходимость в капитальных затратах.

Для перевода качественных параметров в количественные может быть использован, например, ранговый подход или разбиение матрицы экспериментального плана на блоки.

Движение в факторном пространстве к оптимуму возможно, если выбран один единственный параметр оптимизации. При наличии нескольких параметров (например, точность, себестоимость, ресурс) все, кроме одного, выступают уже не параметрами оптимизации, а ограничениями (оптимум ресурса при установленной точности и себестоимости).

Основные требования к параметру оптимизации можно сформулировать в следующем виде:

1 – параметр оптимизации должен быть количественным;

2 – измеряемым;

3 – должен выражаться одним числом (например, соотношение компонентов A : B = 3 : 2 выражается одним числом – 1,5);

4 – быть однозначным в статистическом смысле (заданному набору факторов соответствует одно значение выхода);

5 – эффективным в статистическом смысле, т.е. определяемым с наибольшей достижимой точностью;

6 – существующим для всех исследуемых состояний системы (область его определения может иметь ограничения);

7 – универсальным или обладать полнотой – способностью всесторонне характеризовать объект;

8 – с конкретным физическим смыслом (по возможности);

9 – простым и легко вычисляемым.

Требование физического смысла связано с последующей интерпретацией результатов экспериментов. Легко понять термины "наибольшая производительность" или "точность". Но когда для параметров выхода не выполняется требование статистической эффективности (например, однородность дисперсий), прибегают к преобразованию выхода. Например: ln y или sin 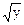и становится неясным, что значит экстремум выхода.

Практически всегда результаты исследования сложных объектов могут быть представлены как задачи с несколькими выходными параметрами. В этом случае можно получить математические модели для каждого параметра выхода, но оптимизировать одновременно несколько функций невозможно.

Из положения можно выйти двумя способами: обосновать отказ от всех выхо-дов, кроме одного, или ввести новый единый обобщенный критерий.

В первом случае можно выбрать одну наиболее важную функцию, исходя из опыта исследователя и целей эксперимента, или воспользоваться данными корреляционного анализа. При этом между всевозможными парами параметров вычисляется коэффициент парной корреляции – мера связи между двумя случайными величинами. Сильная корреляционная связь (более 0,8) при высокой достоверности (обычно 0,95 при числе степеней свободы f = N – 2) позволяет исключить из рассмотрения любой из двух анализируемых параметров как не содержащий дополнительной информации об объекте исследований.

Гораздо перспективнее представляется второй путь – введение обобщенного параметра оптимизации. Для этого необходимо предварительно решить три вопроса:

- привести все параметры выхода к сравнимому безразмерному виду,

- ввести для всех параметров однотипную шкалу измерений,

- выбрать правило объединения нескольких частных откликов в единый обобщенный.

Переменные факторы

Исследование любого объекта – это изучение