Течение совершенного газа через недеформируемый пласт

В данных условиях k = const, h = const, r =r_cт р/ р_ст и

.

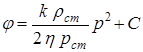Подставляя аналогично предыдущему эти выражения в соответствующие формулы, имеем:

Распределение давления:

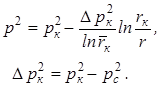(7.17)

Из сравнения следует, что в случае потока газа давление вблизи стенок скважины изменяется более резко, чем при фильтрации несжимаемой жидкости (рисунок 7.6). Пьезометрическая кривая для газа имеет, следовательно, более пологий характер (вдали от скважины) на большем своём протяжении, чем кривая несжимаемой жидкости, однако у неё более резкий изгиб у стенки скважины, чем у кривой несжимаемой жидкости.

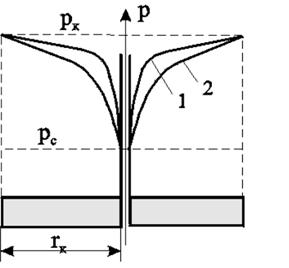
Рисунок 7.6 – Распределение давления при фильтрации идеального газа (кривая 1) и несжимаемой жидкости (кривая 2)

Уравнение массового дебита:

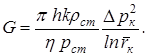
Разделив обе части этого уравнения на r_ст , получим формулу для объёмного дебита, приведенного к стандартному давлению:

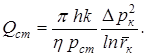(7.18)

Таким образом, индикаторная линия для газа описывает линейную зависимость дебита от разницы квадратов пластового и забойного давлений (в отличие от индикаторной зависимости для несжимаемой жидкости, где устанавливается линейная связь дебита с разницей самих значений пластового и забойного давлений).

Преобразуем уравнение с целью анализа вида данной индикаторной зависимости в координатах Q_ст – (р_к- р_с). Тогда Q_cт=a(р_к²- р_с²), но разность квадратов представим в виде р_к² - р_с²=2р_кDр_с-(Dр_с)², где Dр_с= р_к -р_с. С учётом этого формула дебита перепишется в виде:

р_к² - р_с² = 2р_кDр_с- (Dр_с)².

С учётом этого формула дебита перепишется:

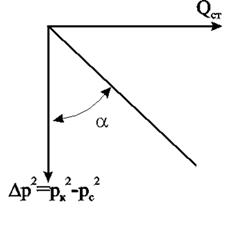
Рисунок 7.7 – Индикаторная зависимость при линейной фильтрации идеального газа

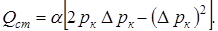(7.19)

Для случая фильтрации совершенного газа по закону Дарси имеем параболу с осью, параллельной оси дебитов. Ветвь параболы, изображенная пунктиром, физического смысла не имеет.

Распределение градиента давления:

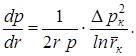(7.20)

Из (7.20) следует, что градиент давления вблизи забоя резко возрастает как за счёт уменьшения r, так и за счёт падения давления р, вызванного сжимаемостью газа.

Изменение скорости фильтрации выведем при использовании уравнения состояния идеального газа:

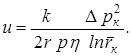(7.21)

Из (7.21) видно, что скорость фильтрации слабо меняется вдали от скважины и резко возрастает в призабойной зоне скважины.

Фильтрация реального газа в недеформируемом пласте

Учет реальных свойств газа следует вести при давлении р_пл >10 МПа и р_с /р_к < 0,9.

Полагаем k = const. Уравнение состояния реального газа при изотермическом течении:

.

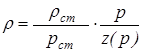Потенциальная функция имеет вид:

,

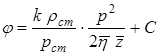где `z = (z<sub>c</sub>+z<sub>к</sub>) / 2; `h = (h_c+h_к) / 2; z_с = z(p_с), h_с =h(p_с), z_к = z(p_к), h_к =h(p_к).

Учтя выражение потенциальной функции, и, перейдя от массового дебита к объёмному ( приведённому к стандартным условиям Q_ст=G/r_cm,получим уравнение притока:

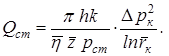(7.22)

Полученное выражение для дебита реального газа отличается от выражения совершенного (идеального) газа среднепластовыми множителями вязкости и сверхсжимаемости `h и `z.