Тема 9. «Прямые и плоскости в пространстве»

9.1. Сторона АВ треугольника АВС лежит в плоскости α. Через середину АС – точку Р

проведена плоскость β, параллельная α и пересекающая ВС в точке Е. РЕ = 9см.

Найти АВ.

9.2. Из точки к плоскости проведены перпендикуляр и наклонная. Длина

перпендикуляра 5см, наклонной 13см. Найти длину проекции наклонной.

9.3. Один конец отрезка лежит в плоскости α, а другой находится на расстоянии 18см

от неё. Чему равно расстояние от середины отрезка до плоскости α

9.4. Отрезок МН не пересекает плоскость α, а МР и НО перпендикуляры к этой

плоскости. МР = 12см, РО = 5см, НО = 24см. Найти МН.

9.5. Плоскость α, параллельная стороне АВ треугольника АВС, пересекает его стороны

в точках М и К. Точка М – середина АС, МК = 42см. Чему равна сторона АВ?

9.6. Из точки А к плоскости проведена наклонная, равная 24см и составляющая угол 30º с этой

плоскостью. Чему равно расстояние от точки А до плоскости?

9.7. Даны две параллельные плоскости и точки А и В на одной из них. Через эти точки

проведены параллельные прямые, пересекающие вторую плоскость в точках М и К.

Чему равен КМ, если АВ = 8см?.

9.8. Отрезки АВ и СD равны и перпендикулярны некоторой плоскости. АС = 34см.

Найти ВD.

9.9. Плоскость α, параллельная основаниям трапеции АВСD, пересекает её боковые

стороны АВ и СD в точках М и К. АD = 36см, ВС = 16см. Чему равен МК, если

т.М – середина АВ?

9.10. Из точки А к плоскости проведена наклонная, составляющая угол 45º с этой плоскостью.

Расстояние от точки А до плоскости 6см. Найти длину наклонной.

9.11. Сторона РК треугольника РКМ лежит в плоскости α. Через середину РМ – точку А

проведена плоскость β, параллельная α и пересекающая КМ в точке Е. АЕ = 25см.

Найти РК.

9.12. Из точки А к плоскости проведена наклонная, составляющая угол 45º с этой плоскостью.

Расстояние от точки А до плоскости 6см. Найти длину наклонной.

9.13. Один конец отрезка лежит в плоскости α, а другой находится на расстоянии 16см

от неё. Найти расстояние от середины этого отрезка до плоскости α

9.14. Отрезки МН и РК равны и перпендикулярны некоторой плоскости. МР = 32см.

Найти НК.

9.15. Плоскость α, параллельная стороне ВЕ треугольника ВЕК, пересекает его стороны

в точках А и С, т.А – середина ВК, ВЕ = 15см. Найти АС.

9.16. Из точки О к плоскости проведена наклонная длиной 14см и составляющая угол

45º с этой плоскостью. Найти расстояние от т.О до плоскости.

9.17. Даны две параллельные прямые и точки С и Е на одной из них. Через эти точки

проведены параллельные плоскости, пересекающие данные прямые в точках А и В.

СЕ = 16см. Найти АВ.

9.18. Отрезок АВ не пересекает плоскость α, АР и ВО – перпендикуляры к этой

плоскости. АР = 6см, АВ = 5см, ВО = 10см. Найти РО.

9.19. Плоскость, параллельная основаниям трапеции, пересекает её боковые стороны в

точках В и С. Найти ВС, если т.В – середина боковой стороны, а основания

трапеции равны 13см и 19см

9.20. Из точки к плоскости проведены перпендикуляр и наклонная. Найти длину проекции наклонной, если длина перпендикуляра 3см, а наклонной 5см.

9.21. Точки А и В лежат по одну сторону от плоскости 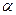на расстояниях 6см и 18см. Найдите расстояние от т.М до плоскости 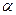, если М – середина АВ.

9.22.Прямые АВ, АС и АD попарно перпендикулярны. Найдите ВС, если AD = 4см, DC = 5см, AB = 4см.

Тема 10. «Многогранники»

10.1. Найти площадь полной поверхности куба, ребро которого равно 3см.

10.2. Найти объём куба, ребро которого равно 2см.

10.3. В основании прямоугольного параллелепипеда лежит ромб, стороны которого 6см

и 8см. Высота параллелепипеда 10см. Найти площадь полной поверхности.

10.4. Длины рёбер прямоугольного параллелепипеда 6см, 8см и 12см. Найти длины его

диагоналей.

10.5. Высота прямой призмы 12см, а её основанием является прямоугольник, стороны

которого 6см и 8см. Найти площадь диагонального сечения призмы.

10.6. Высота правильной треугольной пирамиды равна 6см, а сторона основания 4см. Найти объём

пирамиды.

10.7. Найти полную поверхность правильной четырёхугольной пирамиды, высота

которой равна 2см, а сторона основания 4,2см.

10.8. В правильной четырёхугольной пирамиде высота равна 12см, апофема боковой

грани 13см. Найти боковое ребро.

10.9. Высота правильной четырёхугольной пирамиды 7см, а сторона основания 8см.

Найти боковое ребро пирамиды.

10.10.В правильной четырёхугольной пирамиде высота равна 8см, а боковое ребро

наклонено к плоскости основания под углом 45º. Найти объём пирамиды.

10.11.Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра

равны 13. Найдите площадь поверхности этой пирамиды.

10.12. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5

и 7, боковое ребро равно 4. Найдите объем призмы.

10.13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 3, а

высота равна .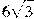

10.14. В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 10. Найдите

ее объем.

10.15. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2 и 7.

Найдите его площадь поверхности.

10.16. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5

и 12, высота призмы равна 8. Найдите площадь ее поверхности.

10.17. Найдите площадь поверхности правильной четырехугольной

пирамиды, стороны основания которой равны 48 и высота равна 7.

10.18. Найдите площадь боковой поверхности правильной четырехугольной пирамиды,

сторона основания которой равна 24 и высота равна 16.

10.19. Найдите объем пирамиды, высота которой равна 3, а основание — прямоугольник со

сторонами 5 и 3.

Тема 11. «Тела вращения»

11.1. Найти объём цилиндра, высота которого 5см, а радиус основания 3см.

11.2. Радиус основания цилиндра 6см, а его образующая 10см. Найти площадь осевого

сечения цилиндра.

11.3. Осевым сечением цилиндра является квадрат, диагональ которого 4см. Найти площадь

полной поверхности цилиндра.

11.4. Прямоугольник, стороны которого 4см и 6см, вращается вокруг большей стороны.

Найти площадь поверхности тела вращения.

11.5. Найти объём конуса, образующая которого 5см, а радиус основания 3см.

11.6. Найти высоту конуса, образующая которого равна 10см, а радиус основания 8см.

11.7. Угол при основании осевого сечения конуса равен 60º, радиус конуса 3см. Найти площадь

боковой поверхности конуса.

11.8. Высота и радиус основания конуса соответственно равны 3см и 4см. Найти

боковую поверхность конуса.

11.9. Образующая конуса наклонена к плоскости основания под углом 45º, а его высота

равна 12см. Найти площадь боковой поверхности конуса.

11.10. Плоскость α касается шара в точке А. Точка С принадлежит плоскости α. Найти площадь

поверхности шара, если АС = 12см, ОС = 13см. ( О – центр шара).

11.11. Найти площадь сечения шара радиуса 5см плоскостью, проведённой на расстоянии

4см от центра.

11.12. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности

цилиндра.

11.13. Найдите объем V конуса, образующая которого равна 3 и наклонена к плоскости основания

под углом 30 .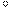

11.14. Высота конуса равна 3, образующая равна 6. Найдите его объем

11.15. Конус получается при вращении равнобедренного прямоугольного треугольника

ABC вокруг катета, равного 15. Найдите его объем.

11.16. Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности.

11.17. Радиус основания конуса равен 28, высота равна 21. Найдите площадь полной поверхности

конуса.